ZL31ARM: implementacja funkcji graficznych 2D
Rysowanie okręgu i koła
Dana operacja wymaga wykorzystania funkcji sinus i cosinus. Można je zrealizować w postaci tablicy wartości dla określonych kątów albo też wykorzystać gotowe sin() i sin(), dostępne w bibliotece z funkcjami matematycznymi math.h., i które przyjmują wartości w radianach.
W danym projekcie zostały wykorzystane gotowe funkcje, jednak jeżeli czas obliczeń jest istotny to można wykorzystać dwie tablice typu float (dostępne w przykładowym rozwiązaniu): sinus[] i cosinus[]. W tym przypadku pomocną okaże się funkcja konwertująca kąt zadawany w stopniach na indeks elementu w tablicy:
unsigned char Deg2Index(signed short angle){
if(abs(angle) >= 360)
angle = angle % 360; //Na wypadek wystapienia kata >=360 stopni
if(angle >= 0)
angle = (unsigned char) 128*abs(angle)/360;
else if(angle < 0)
angle = 128 - (unsigned char) 128*abs(angle)/360;
return angle;
}
Funkcja przyjmuje wartości (również ujemne) kąta w stopniach i w razie potrzeby konwertuje ją do przedziału od 0 do ±359 stopni. Dalej obliczany jest indeks odpowiedniego elementu w tablicy i w zależności od tego czy kąt jest ujemny czy dodatni, indeks jest brany odpowiednio od końca lub od początku tablicy.
Rysowanie okręgu/koła polega na podaniu punktu środkowego oraz promienia. Oprócz tego funkcja przyjmuje 2 dodatkowe parametry, tak jak poprzednio, kolor i styl (w przypadku przekazania 1 jest rysowane koło wypełniane zadanym kolorem). Okrąg jest budowany przez wyznaczanie kolejnych punktów na obwodzie i ich łączeniu. Natomiast rysowanie koła wykonuje się za pomocą funkcji drawLine(), która to rysuje kolejne linie zawarte na płaszczyźnie ograniczonej przez obwód koła i w efekcie otrzymuje się zapełnioną zadanym kolorem figurę. Struktura funkcji drawCircle() jest następująca:
void drawCircle(int x0, int y0, int r, unsigned int color, unsigned char style){
unsigned short alpha = 360; //Pelny kat poczatkowy
unsigned int i;
signed int xp, yp, xn, yn; //Zmienne tymczasowe
switch(style){
//Rysuj kolo z wypelnieniem zadanym kolorem
case(1):{
for(i=0; i < 2*r; i++){
yn = (int) sqrt(r*r - abs(r-i)*abs(r-i)); //Z tw. Pitagorasa
drawLine(x0-r+i,y0+yn,x0-r+i,y0-yn,color);
}
}
//Rysuj okrag z zadanym kolorem
default:{
//Wartosci poczatkowe - poprzednie
xp = r;
yp = 0;
//Rysuj punkty na okregu co 1 stopien
while(alpha != 0){
//Nowe wartosci obroconego punktu na okregu
xn = (int) r*cos(alpha*6.28318/360);
yn = (int) r*sin(alpha*6.28318/360);
//Polacz punkt poprzedni i kolejny
drawLine(xp+x0,yp+y0,xn+x0,yn+y0,color);
//Zachowaj stare wspolrzedne
xp = xn;
yp = yn;
alpha--; //Kolejny kat
}
}
}
}
W celu zobrazowania działania funkcji można wykonać następujący przykład:
// Rysowanie pustych okregow testowych drawCircle(-30, 30, 30,RED); drawCircle( 0, 0, 20,GREEN); drawCircle( 30,-30, 10,BLUE);
lub:
// Rysowanie kolorowych kol testowych drawCircle(-30, 30, 30,RED,1); drawCircle( 0, 0, 20,GREEN,1); drawCircle( 30,-30, 10,BLUE,1);
Rysowanie elipsy i owalu
Funkcja realizująca daną operację jest bardzo podobna do poprzedniej, jednak w obecnym przypadku zamiast podawania jednego promienia należy podać ich dwa. Pierwszy jest liczony w kierunku osi x (parametr a), a drugi w osi y (parametr b). Mimo takiej samej metody rysowania konturu figury jak w przypadku poprzednim (z wyjątkiem występowania dwóch promieni), sposób rysowania wraz z wypełnianiem jest nieco inne, a mianowicie różnica polega na zastosowaniu innego wzoru w postaci kanonicznej:
Niżej przedstawiono kod funkcji drawEllipse():
void drawEllipse(int x0, int y0, int a, int b, unsigned int color,
unsigned char style){
unsigned short alpha = 360;
signed int i;
signed int xp, yp, xn, yn; //Zmienne tymczasowe
switch(style){
//Rysuj owal z wypelnieniem zadanym kolorem
case(1):{
for(i=0; i < 2*a; i++){
yn = (int) sqrt( b*b*( 1.0 - ( (float) (i-a)*(i-a))/(a*a) ) );
drawLine(x0-a+i,y0+yn,x0-a+i,y0-yn,color);
}
}
//Rysuj elipse z zadanym kolorem
default:{
//Wartosci poczatkowe - poprzednie
xp = a;
yp = 0;
//Rysuj punkty na okregu co 1 stopien
while(alpha != 0){
//Nowe wartosci wspolrzednych punktu na obwodzie elipsy
xn = (int) a*cos(alpha*6.28318/360);
yn = (int) b*sin(alpha*6.28318/360);
//Polacz punkt poprzedni i kolejny
drawLine(xp+x0,yp+y0,xn+x0,yn+y0,color);
//Zachowaj stare wspolrzedne
xp = xn;
yp = yn;
alpha--; //Kolejny kat
}
}
}
}






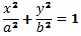
 Caroline Pannier – nowa dyrektorka targów electronica – analizuje sytuację gospodarczą branży i przedstawia wyniki
Caroline Pannier – nowa dyrektorka targów electronica – analizuje sytuację gospodarczą branży i przedstawia wyniki  Konstrukcja Ventiva Zoned Cooling™ – ukierunkowane chłodzenie powietrza dla urządzeń AI Edge
Konstrukcja Ventiva Zoned Cooling™ – ukierunkowane chłodzenie powietrza dla urządzeń AI Edge  Komunikacja dalekiego zasięgu oparta na technologii Qualcomm dla robotyki i dronów
Komunikacja dalekiego zasięgu oparta na technologii Qualcomm dla robotyki i dronów 






