ZL31ARM: funkcje graficzne 3D
Na początku pliku graphics.c jest zdefiniowana struktura zawierająca współrzędne początku i końca linii w przestrzeni 3D:
typedef struct{
float x1, y1, z1, x2, y2, z2;
} line3D;
Zostanie ona wykorzystana w tablicy typu line3D[] przechowującej krawędzie sześcianu:
line3D rotatedCube[12], cube[12]={
{-CWH, CWH,-CWH,-CWH, CWH, CWH}, // 1 krawedz
..
{-CWH, CWH, CWH, CWH, CWH, CWH} // 12 krawedz
};
gdzie CWH to CUBE_WIDTH_HALF, czyli połowa długości boku, zdefiniowana na początku pliku jako:
#define CUBE_WIDTH_HALF 20
Właściwie to są tworzone dwie tablice, z których cube[] zawiera stałe wartości wykorzystywane podczas transformacji, a rotatedCube[] będzie zawierał wynik tychże transformacji, które mogą się zmieniać w czasie działania programu.
Aby teraz narysować bryłę należy wykonać poniższe instrukcje:
//Rysuj kolejne krawedzie szescianu for(i=0; i < 12; i++) drawLine(cube[i].x1, cube[i].y1, cube[i].x2, cube[i].y2, color);
Obrót i przesunięcie sześcianu
W celu dokonania obrotu bryły należy obrócić wszystkie linie tworzące krawędzie, które potem zostaną narysowane. Jest to robione za pomocą funkcji rotateLine() w pętli for:
//Obroc wszystkie 12 krawedzi szescianu for (i=0; i < 12; i++) rotateLine(cube[i], &(rotatedCube[i]), x_angle, y_angle, z_angle);
Funkcja ta przyjmuje jako argumenty: strukturę wartości współrzędnych końcowych linii do obrócenia, wskaźnik do struktury w której zostaną zapisane przetransformowane współrzędne, oraz 3 kąty obrotu względem kolejnych osi układu OXYZ. Jej definicja wygląda następująco:
void rotateLine(line3D ToRotate, line3D * Rotated,
signed short x_angle, signed short y_angle, signed short z_angle){
//Obrot wzgledem osi Z w plaszczyznie XY
rotatePoint(ToRotate.x1, ToRotate.y1, z_angle, &(*Rotated).x1, &(*Rotated).y1);
rotatePoint(ToRotate.x2, ToRotate.y2, z_angle, &(*Rotated).x2, &(*Rotated).y2);
//Obrot wzgledem osi X w plaszczyznie YZ
rotatePoint(ToRotate.z1, (*Rotated).y1, x_angle, &(*Rotated).z1, &(*Rotated).y1);
rotatePoint(ToRotate.z2, (*Rotated).y2, x_angle, &(*Rotated).z2, &(*Rotated).y2);
//Obrot wzgledem osi Y w plaszczyznie XZ
rotatePoint((*Rotated).x1, (*Rotated).z1, y_angle, &(*Rotated).x1, &(*Rotated).z1);
rotatePoint((*Rotated).x2, (*Rotated).z2, y_angle, &(*Rotated).x2, &(*Rotated).z2);
}
Ostatnia funkcja, która realizuje elementarny obrót punktów, o zadany kąt, wykorzystuje dwie zależności matematyczne:
i jest zaimplementowana następująco:
void rotatePoint(int x, int y, signed short angle, int * resx, int * resy){
if(abs(angle) >= 360)
angle = angle % 360; //Na wypadek wystapienia kata >=360 stopni
*resx = x * cos(angle*6.28318/360) - y * sin(angle*6.28318/360);
*resy = x * sin(angle*6.28318/360) + y * cos(angle*6.28318/360);
}
Pierwsze dwa argumenty funkcji to wartości aktualne współrzędnych punktu na określonej powierzchni, kolejny parametr to zadany kąt obrotu, a ostatnie dwa to wskaźniki na zmienne typu float do których zostaną zapisane nowe, przetransformowane wartości współrzędnych.
Efekt działania takiego kodu można sprawdzić za pomocą wywołania funkcji drawCube(), której struktura wygląda następująco:
void drawCube(int x0, int y0, unsigned char x_angle, unsigned char y_angle,
unsigned char z_angle, unsigned int color){
unsigned char i;
//Obroc wszystkie 12 krawedzi szescianu
for (i=0; i < 12; i++)
rotateLine(cube[i], &(rotatedCube[i]), x_angle, y_angle, z_angle);
//Rysuj kolejne krawedzie szescianu
for(i=0; i < 12; i++)
drawLine(x0 + rotatedCube[i].x1, y0 + rotatedCube[i].y1, x0 +
rotatedCube[i].x2, y0 + rotatedCube[i].y2, color);
}





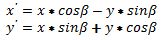
 Platforma JetSys-2010 SFF do wysokowydajnych obliczeń AI-at-the-EDGE w aplikacjach high-end
Platforma JetSys-2010 SFF do wysokowydajnych obliczeń AI-at-the-EDGE w aplikacjach high-end  Hahn EI30 ErP – transformatory sieciowe o niskich stratach mocy
Hahn EI30 ErP – transformatory sieciowe o niskich stratach mocy  Grzegorz Kamiński: Co nowego na rynku podzespołów półprzewodnikowych GaN?
Grzegorz Kamiński: Co nowego na rynku podzespołów półprzewodnikowych GaN? 


![https://www.youtube.com/watch?v=kmvM5hVSzCM Piata już edycja konferencji Hardware Design Masterclasses dla elektroników zaskoczyła frekwencją, tym bardziej, że spotkanie było dwudniowe. Film jest krótką relacją z wydarzenia, bazującą na wypowiedziach prelegentów. [materiał redakcyjny] Zapraszamy do obejrzenia!](https://mikrokontroler.pl/wp-content/uploads/2026/01/Rafal-tytulowe.png)

