Implementacja algorytmów sterowania silnikami DC w XMC4000

Transformacja Clarka:

Transformacja Parka:

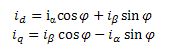
Gdy wartości i _d oraz i _q są już znane, powinny zostać przetworzone przez regulator PI. Regulator PI jest odmianą regulatora proporcjonalno-całkująco-różniczkującego (PID – proportional-integral-derivative controller ), różniąc się od niego tym, że blok różniczkujący nie jest używany (K _D ma wartość zero). Jeden regulator PI steruje prądem i _d sprowadzając jego wartość do zera i zapewniając kąt 90 stopni pomiędzy strumieniem stojana i wirnika. Drugi regulator PI steruje prądem i _q ustalając jego zadeklarowaną wartość.

Biblioteka CMSIS DSP zawiera implementację stałoprzecinkową i zmiennoprzecinkową transformacji Clarka i Parka, jak również kontrolera PID. Na rysunku 5 zilustrowano schemat blokowy regulatora PI. Sygnał e(t) jest różnicą pomiędzy zadaną wartością i _d oraz i _q i aktualną wartością i _d oraz i _q, które są wyliczone przy pomocy zmierzonych prądów stojana i pozycji wirnika.  

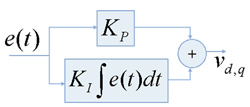
Rys. 5. Kontroler PI

Należy zauważyć, że wyjściem regulatorów PI są wartości napięcia v _d oraz v _q. Nie można ich bezpośrednio przełożyć na parametry sygnału PWM.

Istnieje wiele sposobów, aby zamienić napięcia v _d oraz v _q na sygnały 3-fazowego falownika. Jedną z nich jest SVM ( Space Vector Modulation ). v _d oraz v _q są powiązane z pozycją  wirnika. Należy wykonać rozkład tych wektorów na wektory napięcia, które mogą być generowane przez 3-fazowy falownik.

Na rysunku 6 pokazano przykład 3-fazowego falownika. Każdy wektor napięcia powstaje poprzez włączenie jednego sterownika typu „high-side switch” oraz dwóch sterowników typu „low-side switch”, bądź dwóch sterowników typu „high-side switch” oraz jednego sterownika typu „low-side switch”. Wektory napięcia oraz odpowiadające wygenerowaniu ich stany falownika pokazano na rysunku 7.

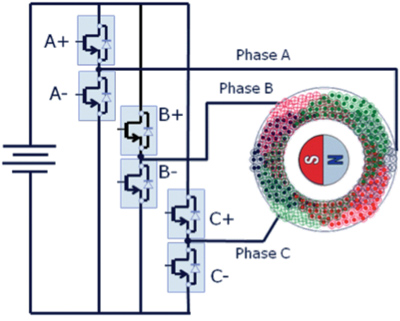
Rys. 6. 3-fazowy falownik połączony z 3-fazowym silnikiem PMSM

Uzyskanie rozkładu v _d i v _q na wektory napięć przeprowadzone zostanie w dwóch etapach. Pierwszy etap to wykonanie odwrotnej transformacji Parka ( Inverse Park Transform ). Jak nazwa wskazuje, zamienia ona v _d i v _q na v _α oraz v _β, co pokazano na rysunku 7 (A). Odwrotna transformacja Parka została zaimplementowana w bibliotece CMSIS DSP.

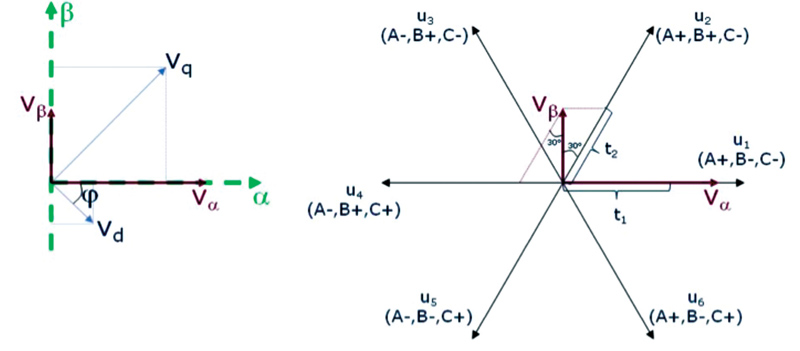
Rys. 7. Rysunek A pokazuje przekształcenie v _d i v _q na v _α oraz v _β za pomocą odwrotnej transformacji Parka, natomiast rysunek B pokazuje przekształcenie v _α i v _β na stany sterowników

Odwrotna transformacja Parka:

Gdy wartości v _α i v _β są znane, mogą zostać przekształcone na wektory stanów sterowników (wybierany jest wektor najbliższy sumie v _α i v _β ). Poniżej przedstawiono wzory stosowane w przypadku, gdy wektor sumy  v _α i v _β zawiera się pomiędzy u ₁ i u ₂ :

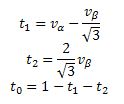
t ₁ i t ₂ to procent czasu, przez jaki aktywny powinien być odpowiednio pierwszy i drugi wektor najbliższy sumie v _α i v _β. W przypadku gdy t ₁ + t ₂ < 100%, pozostaje trochę czasu, który nazwany jest t ₀. W jego trakcie wszystkie sterowniki mogą pozostawać w stanie włączenia.