Sygnały kwadraturowe, nazywane też sygnałami, danymi lub próbkami IQ są często wykorzystywane w systemach radiowych. Stanowią podstawę modulacji i demodulacji zespolonych sygnałów RF, realizowanych zarówno sprzętowo, jak i programowo, a także analiz takich sygnałów. Niniejszy artykuł przybliża podstawowe koncepcje stojące za sygnałami IQ oraz ich zastosowania. Mówimy, że dwa sygnały okresowe są kwadraturowe (lub w kwadraturze), gdy są w stosunku do siebie przesunięte w fazie o 90o. Sygnał odniesienia, będący „w fazie” oznaczany jest literą „I”, a sygnał przesunięty o 90o (czyli będący w kwadraturze do I), oznaczany jest „Q”. Co to oznacza i dlaczego nas obchodzi? Przyjrzyjmy się temu zaczynając od podstaw.
| Chcesz być na czasie?
Tematyka SDR jest coraz ważniejsza we współczesnej elektronice, poświęciliśmy jej kilka ważnych artykułów, których wykaz jest dostępny pod tym linkiem. |
Podstawy modulacji RF
Rozpoczniemy od omówienia prostej modulacji RF. Niezmodulowana nośna, przedstawiona na poniższym rysunku, to zwykła sinusoida.
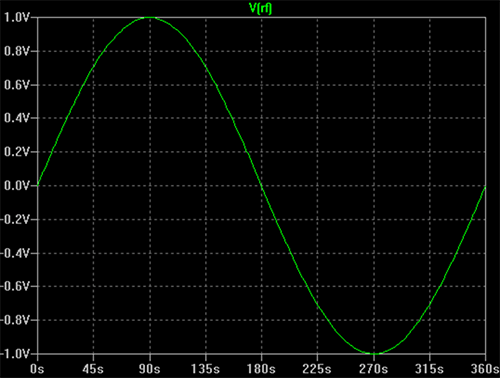
Sygnał można opisać jako funkcję czasu daną równaniem: V(t) = A * sin (2 * π * f * t + Ф), gdzie: A oznacza amplitudę, f to częstotliwość, t to czas a Ф to przesunięcie fazowe.
Informacja jest „przenoszona” przy pomocy nośnej dzięki procesowi modulacji – sygnał informacyjny (głos, dane, itp.) jest używany do zmiany właściwości sygnału RF. Prostym przykładem takiego zabiegu jest modulacja amplitudy, nazywana w skrócie AM (Amplitude Modulation).
W modulacji AM sygnał informacyjny jest używany do zmiany amplitudy nośnej. Matematycznie rzecz biorąc, można to zapisać jako zamianę stałej A z wcześniejszego równania na wielkość zależną od czasu (w naszym przypadku jest to sygnał informacyjny):
V(t) = A(t) * sin (2 * π * f * t + Ф)
Sygnał informacyjny, nazywany też sygnałem w paśmie podstawowym (baseband signal) zmienia się dużo wolniej, niż sygnał RF, więc by zaobserwować wpływ modulacji trzeba się przyjrzeć obwiedni sygnału RF w dłuższym okresie, której przykład przedstawia poniższy rysunek.
W powyższym przypadku sygnał A(t) jest sinusoidalny. Rysunek przedstawia, jak amplituda sygnału RF podąża za zmianami sinusoidalnego sygnału w paśmie podstawowym A(t).
Rozważania można rozszerzyć zauważając, że zmianom, czyli modulacji, mogą podlegać także inne własności sygnału RF. Jeśli modulowana jest częstotliwość mamy do czynienia z modulacją FM (Frequency Modulation). Jeśli zmianom ulega faza, stosowana jest modulacja PM (Phase Modulation). Wracając do podstawowego wzoru, musimy więc podstawić:
- A(t), jeśli w czasie zmienia się amplituda,
- F(t), jeśli zmienia się częstotliwość,
- Ф(t), jeśli zmienia się faza.
Warto rozumieć i pamiętać podstawową koncepcję modulacji, gdy wprowadzamy pojęcie sygnałów kwadraturowych.
Koncepcja sygnałów kwadraturowych
Jeśli różnica fazy miedzy dwiema sinusoidami wynosi 90o (lub π/2 radianów), mówimy że sygnały te są w kwadraturze. Przykładem takiej pary sygnałów są sinusoida i kosinusoida.
Przyjmuje się, że sygnał kosinusoidalny jest w fazie, a sinusoida jest składową kwadraturową. Wielka litera „I” oznacza amplitudę sygnału w fazie, a wielka litera „Q” oznacza amplitudę sygnału kwadraturowego.
Wykorzystywanie sygnałów kwadraturowych do modulacji
Ciekawa rzecz dzieje się, gdy sygnały będące w kwadraturze dodamy do siebie.
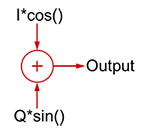
Jeśli I=1 oraz Q=0, otrzymujemy sygnał kosinusoidalny (o zerowym przesunięciu fazowym). Analogicznie, gdy I=0, a Q=1, otrzymujemy sygnał sinusoidalny, przesunięty w fazie o 90o.
Jeśli zarówno I, jak i Q są równe 1, otrzymujemy nowy sygnał, przedstawiony graficznie poniżej.
Warto zauważyć, że suma dwóch sygnałów o takiej samej amplitudzie, będących w kwadraturze jest sinusoidą przesuniętą w fazie o 45o.
Zapewne widoczne jest już, że amplituda i faza sumy sygnałów kwadraturowych jest funkcją wartości I oraz Q, a więc można tworzyć zmodulowane sygnały RF, zmieniając te wartości w czasie. Przyjrzyjmy się kilku przykładom.
Przykłady cyfrowych modulacji RF
Jeśli Q=0, a wartość I jest przełączana skokowo od +1 do -1, uzyskujemy sygnał z binarnym kluczowaniem fazy, nazywany też BPSK (Binary Phase Shift Keyed):
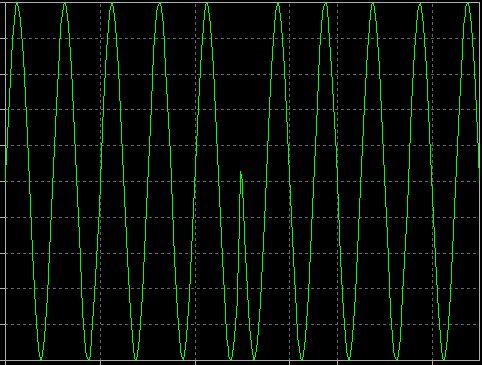
Sygnał I(t) może być np. prostym strumieniem bitów – gdy użyjemy takiego sygnału do sterowania amplitudą sinusoidalnego sygnału RF od –1 do +1 uzyskamy modulację BPSK.
Pójdźmy krok dalej. Jeśli dwa bity są używane do zmiany wartości I oraz Q w czasie od +1 do -1, suma sygnałów kwadraturowych może mieć jedno z czterech przesunięć fazowych:
- I=+1 oraz Q=+1 skutkuje przesunięciem 45o,
- I=-1 oraz Q=+1 skutkuje przesunięciem 135o,
- I=-1 oraz Q=-1 skutkuje przesunięciem 225o,
- I=+1 oraz Q=-1 skutkuje przesunięciem 315o.
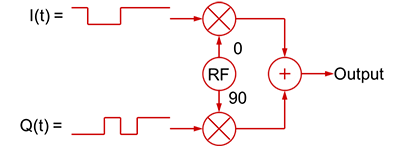
Technika ta nosi nazwę kwadraturowego kluczowania fazy i jest szerzej znana jako QPSK (Quadrature Phase Shift Keying). Obie te modulacje są przykładami kwadraturowych modulacji amplitudy, zwanych często QAM (Quadrature Amplitude Modulation). Różne stany sygnału zmodulowanego QAM przedstawia się często na tzw. diagramie konstelacji. Jest to diagram fazowy, przedstawiający amplitudę i fazę sygnału na płaszczyźnie zespolonej.
Długość wektora od początku układu współrzędnych reprezentuje amplitudę sygnału, a kąt tworzony przez wektor z osią poziomą oznacza fazę. Cztery „stany” sygnału QPSK opisane powyżej są na diagramie przedstawione jako cztery plusy. Można też zauważyć, że oś pozioma jest oznaczona „I”, a oś pionowa „Q”. Jest tak, gdyż reprezentują one składowe I oraz Q sygnału sumarycznego.
Bardziej złożone typy modulacji QAM, takie jak 16QAM, mają po prostu więcej dopuszczalnych stanów. Dla 16QAM I oraz Q przyjmują po cztery wartości, co daje łącznie 16 możliwych kombinacji amplitudy i fazy sumarycznego sygnału RF.
