[RAQ] Wartość średniokwadratowa mocy vs. moc średnia
Pytanie:
Czy powinienem użyć jednostek mocy średniokwadratowej (rms), aby określić moc prądu przemiennego związaną z sygnałem, systemem lub urządzeniem?
Odpowiedź:
Zależy to od sposobu definiowania mocy skutecznej.
Nie należy obliczać wartości średniokwadratowej przebiegu mocy prądu przemiennego. Daje to wynik, który nie ma fizycznego sensu.
Do obliczenia średniej mocy używa się wartości skutecznych napięcia i/lub prądu. W ten sposób uzyskamy znaczące wyniki.
Omówienie
Ile mocy wydzieli się na rezystorze 1 Ω, gdy podamy na nie sinusoidalne napięcie o wartości 1 V rms?
Powyższy wzór jest dobrze rozumiany1 i nie ma w nim nic zaskakującego.
Zobaczmy teraz, czy ta wartość jest porównywalna z wartością otrzymaną z obliczenia mocy skutecznej.
Rysunek 1 pokazuje wykres sinusoidy 1 V rms. Wartość międzyszczytowa wynosi 1 V rms × 2 √2 = 2,828 V, a napięcie zmienia się od +1,414 V do –1,414 V 2.
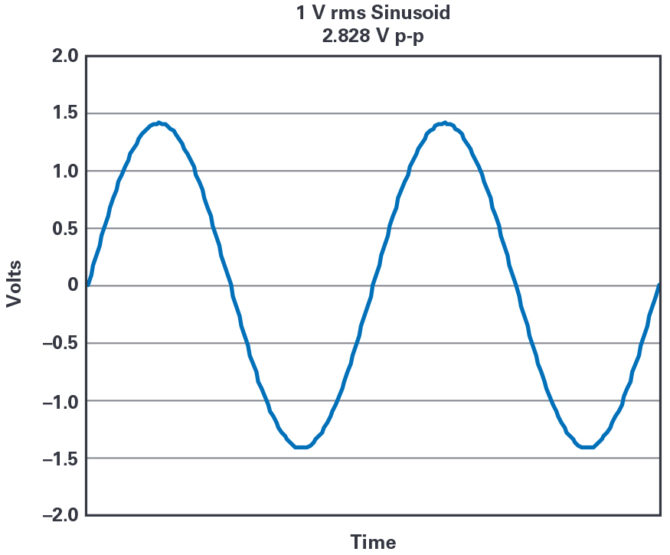 Rysunek 1. Wykres sygnału sinusoidalnego 1 V rms
Rysunek 1. Wykres sygnału sinusoidalnego 1 V rms
Rysunek 2 jest wykresem mocy rozproszonej przez sinusoidę o wartości skutecznej 1 V na oporniku 1 Ω (P = V2/R).
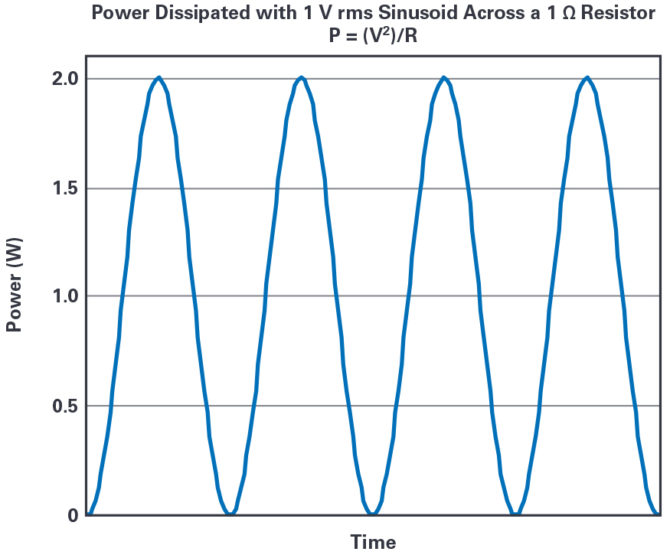 Rysunek 2. Wykres mocy rozproszonej przez sinusoidę o wartości skutecznej 1 V na oporniku 1 Ω
Rysunek 2. Wykres mocy rozproszonej przez sinusoidę o wartości skutecznej 1 V na oporniku 1 Ω
Z wykresu wynika, że:
- Krzywa mocy chwilowej ma średnią 1 W i zmienia się od 0 W do 2 W.
- Wartość skuteczna tego przebiegu mocy wynosi 1,225 W.
- Jedną z metod obliczania tej liczby jest równanie 23:
-
- Można to zweryfikować za pomocą bardziej szczegółowej formuły4 w MATLABie lub Excelu.
- Średnia wartość tego przebiegu mocy wynosi 1 W. Jest to oczywiste; przebieg waha się symetrycznie powyżej i poniżej 1 V. Ta sama wartość wynika z obliczenia średniej liczbowej punktów na wykresie.
- Średnia wartość mocy odpowiada mocy obliczonej na podstawie napięcia skutecznego.
Znaczenie mocy średniej
Moc rozproszona przez sinusoidalną wartość skuteczną 1 V na rezystorze 1 Ω wynosi 1 W, a nie 1,225 W. Zatem średnia moc wytwarza prawidłową wartość, przez co ma znaczenie fizyczne. Moc skuteczna (zdefiniowana powyżej) nie ma oczywistego użytecznego znaczenia (nie ma oczywistego znaczenia fizycznego/elektrycznego), poza tym, że jest wielkością, której obliczenie można traktować jako ćwiczenie.
Można w łatwy sposób wykonać tą samą analizę dla prądu sinusoidalnego o wartości 1 A rms na rezystorze 1 Ω. Wynik jest taki sam.
Zasilacze do układów scalonych na ogół wytwarzają napięcie stałe, dlatego moc skuteczna nie stanowi wtedy problemu. W przypadku prądu stałego wartość średnia i skuteczna mają taką samą wartość. Znaczenie używania mocy średniej, w przeciwieństwie do mocy skutecznej, zgodnie z definicją zawartą w tym artykule, dotyczy mocy związanej ze zmieniającym się w czasie napięciem i prądem – to znaczy szumem, sygnałami RF, a także oscylatorami.
Zaleca się użycia wartości skutecznej napięcia i/lub wartości skutecznej prądu do obliczenia mocy średniej, co da sensowne wartości mocy.
Przypisy:
1 Moc wydzielana z napięcia na rezystorze jest podstawową zależnością, którą łatwo wyprowadzić z prawa Ohma (V = IR) oraz podstawowych definicji napięcia (energia / ładunek elektryczny) i prądu (ładunek elektryczny / czas). Oznacza to, że napięcie × prąd = energia / czas = moc.
2 Wartość międzyszczytowa sinusoidy jest wartością skuteczną pomnożoną przez 2√2. Dla napięcia sinusoidalnego V p-p = V rms × 2√2, gdzie V p-p jest napięciem międzyszczytowym, a V rms jest napięciem skutecznym. Jest to dobrze znana relacja udokumentowana w niezliczonych podręcznikach, a także tutaj: pl.wikipedia.org/wiki/Średnia_kwadratowa.
3 Równanie zostało obliczone na podstawie wartości skutecznej obliczonej ze składowej stałej prądu plus wartości skutecznej prądu przemiennego, a także z noty aplikacyjnej Keysight Technologies “Make Better AC RMS Measurements with Your Digital Multimeter”
4 Standardowa podręcznikowa definicja jest bardziej szczegółowa:







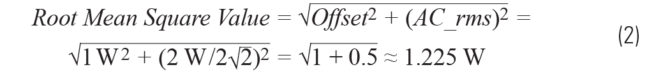

 Caroline Pannier – nowa dyrektorka targów electronica – analizuje sytuację gospodarczą branży i przedstawia wyniki
Caroline Pannier – nowa dyrektorka targów electronica – analizuje sytuację gospodarczą branży i przedstawia wyniki  Konstrukcja Ventiva Zoned Cooling™ – ukierunkowane chłodzenie powietrza dla urządzeń AI Edge
Konstrukcja Ventiva Zoned Cooling™ – ukierunkowane chłodzenie powietrza dla urządzeń AI Edge  Komunikacja dalekiego zasięgu oparta na technologii Qualcomm dla robotyki i dronów
Komunikacja dalekiego zasięgu oparta na technologii Qualcomm dla robotyki i dronów 






