W artykule opisujemy pomiar częstotliwości rezonansu własnego cewki indukcyjnej wykonany w formie ćwiczenia laboratoryjnego.

Wprowadzenie

Cewki indukcyjne, które stosujemy powszechnie w różnych układach elektronicznych podobnie jak wszystkie rzeczywiste elementy elektryczne, nie są idealne. Na rys. 1 został pokazany najczęściej spotykany schemat prostego modelu rzeczywistej cewki indukcyjnej. Oprócz pożądanej indukcyjności L, element ten ma również straty (modelowane przez rezystancję szeregową przedstawioną na schemacie jako R) i równoległą pojemność pasożytniczą, pokazaną jako C. Im mniejsza rezystancja, która w cewce idealnej jest równa 0 Ω, i im mniejsza pojemność, która w idealnym elemencie jest równa 0 F, tym bardziej idealna staje się cewka indukcyjna.

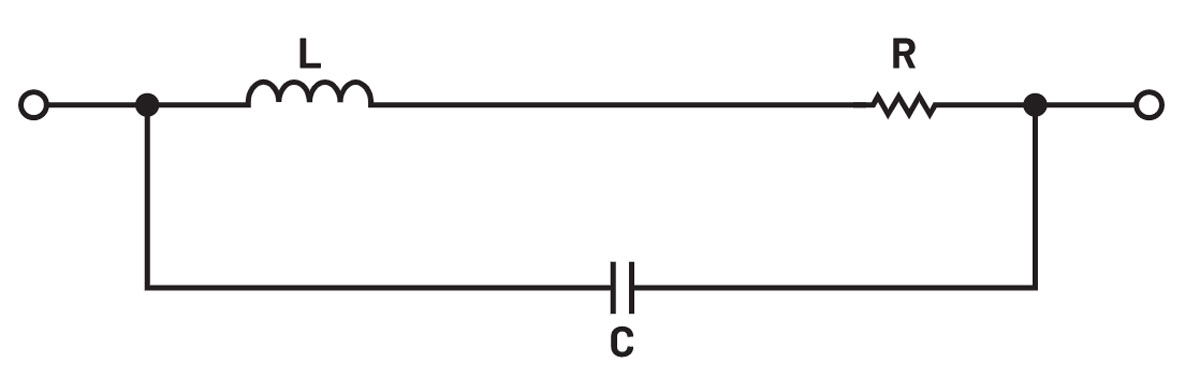
Rys. 1. 3-lementowy model LRC cewki indukcyjnej

Pojemność międzyzwojowa i częstotliwość rezonansu własnego

Klasyczny opis pojemności C jest taki, że reprezentuje ona rozproszoną pojemność międzyzwojową (i inne pojemności pasożytnicze) cewki indukcyjnej. Przy pewnej częstotliwości, SRF, pojemność ta przyczynia się do wytworzenia rezonansu równoległego z indukcyjnością L, a cała cewka indukcyjna staje się obwodem rezonansowym dostrojonym do tej częstotliwości.

Impedancja 3-elementowego modelu LRC w funkcji częstotliwości

Przy częstotliwościach poniżej SRF model ma charakter indukcyjny. Przy częstotliwościach powyżej SRF cewka nabiera charakteru pojemnościowego, a dokładnie przy SRF jest czysto rezystancyjna, ponieważ reaktancja indukcyjna i pojemnościowa są równe co do wielkości, ale przeciwne co do znaku, a zatem znoszą się.

Przy SRF cewki indukcyjnej spełnione są wszystkie poniższe warunki:

• Impedancja wejściowa jest szczytowa;
• Kąt fazowy impedancji wejściowej wynosi zero, przechodząc od dodatniego (indukcyjnego) do ujemnego (pojemnościowego);
• Ponieważ kąt fazowy wynosi zero, Q wynosi zero;
• Efektywna indukcyjność wynosi zero, ponieważ ujemna reaktancja pojemnościowa (X_C = -j/ωC) po prostu znosi dodatnią reaktancję indukcyjną (X_L = jωL);
• 2-portowa tłumienność wtrąceniowa (S21 dB) jest maksymalna, co odpowiada minimum na wykresie częstotliwości w funkcji S21 dB;
• Faza 2-portowa (kąt S21) wynosi zero, przechodząc od ujemnej przy niższych częstotliwościach do dodatniej przy wyższych częstotliwościach.

Poniższe równanie pokazuje, w jaki sposób parametr SRF jest powiązany z indukcyjnością i pojemnością w obwodzie przedstawiającym model cewki indukcyjnej.

gdzie:

L to indukcyjność w henrach

Cp jest pasożytniczą pojemnością w faradach

Z równania jasno wynika, że zwiększenie indukcyjności lub pojemności obniża zmierzony SRF, a zmniejszenie indukcyjności lub pojemności podnosi SRF.

Symulacja wstępna 3-elementowego modelu cewki indukcyjnej LRC

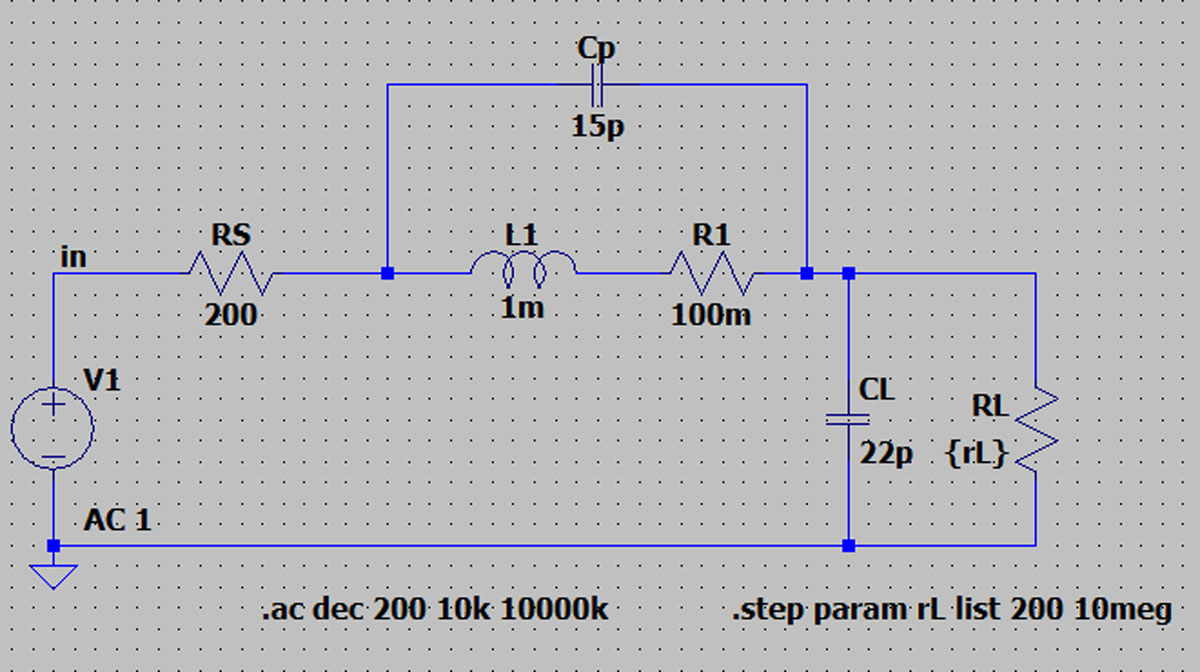
Schemat przedstawiony na rys. 2 to obwód testowy symulacji dla 3-elementowego modelu LRC cewki indukcyjnej. Elementy L1, R1 i C_P są używane do modelowania cewki indukcyjnej. V1 jest idealnym źródłem napięcia testowego AC, a rezystor RS służy jako rezystancja źródła V1. CL i RL są składowymi obciążenia, przy czym CL jest ustawiony jako typowa pojemność wejściowego kanału pomiarowego. RL jest równy RS lub może być ustawiony na wyższą wartość, taką jak typowa rezystancja wejściowa 1 MΩ kanału pomiarowego.

Rys. 2. Schemat symulacji

Przed zbudowaniem rzeczywistego obwodu testowego cewki indukcyjnej należy przeprowadzić symulację układu pokazanego na rys. 2.

Jak pokazano na rys. 3, przeprowadzono dwie symulacje przemiatania częstotliwości od 10 kHz do 10 MHz jako przykład cewki indukcyjnej L 1 mH z C_P równą 15 pF i R 100 mΩ. Linia zielona to spadek napięcia na RL=200 Ω (tyle samo co RS). Amplituda obserwowana dla RL ma ostry spadek przy SRF, gdy impedancja cewki indukcyjnej osiąga maksimum. Niebieska krzywa przedstawia spadek napięcia na RL, który jest w tym przypadku równy 1 MΩ (oporność wejścia pomiarowego przyrządu). Ponownie widzimy ostre zero, gdy impedancja jest maksymalna, a także ostry szczyt amplitudy obserwowany przy RL około oktawy poniżej wycięcia. Ten szczyt występuje, gdy rezystancje źródła i obciążenia nie są dopasowane.

Rys. 3. Wyniki symulacji: Czerwona krzywa RL = 200 Ω, niebieska krzywa RL = 1 MΩ

Materiały

• – Pomiarowy zestaw edukacyjny Analog Discovery 2;
• – Stykowa płytka prototypowa z zestawem przewodów połączeniowych;
• – Cewka indukcyjna 1 mH;
• – ewentualnie cewki indukcyjne o różnych indukcyjnościach;
• – Dwa rezystory 200 Ω.

Wskazówki

Zbuduj obwód testowy cewki indukcyjnej na płytce prototypowej, jak pokazano na rys. 4. Niebieskie kwadraty wskazują miejsca podłączenia wejścia AWG zestawu Analog Discovery i kanałów pomiarowych.

Rys. 4. Układ testowy cewki indukcyjnej

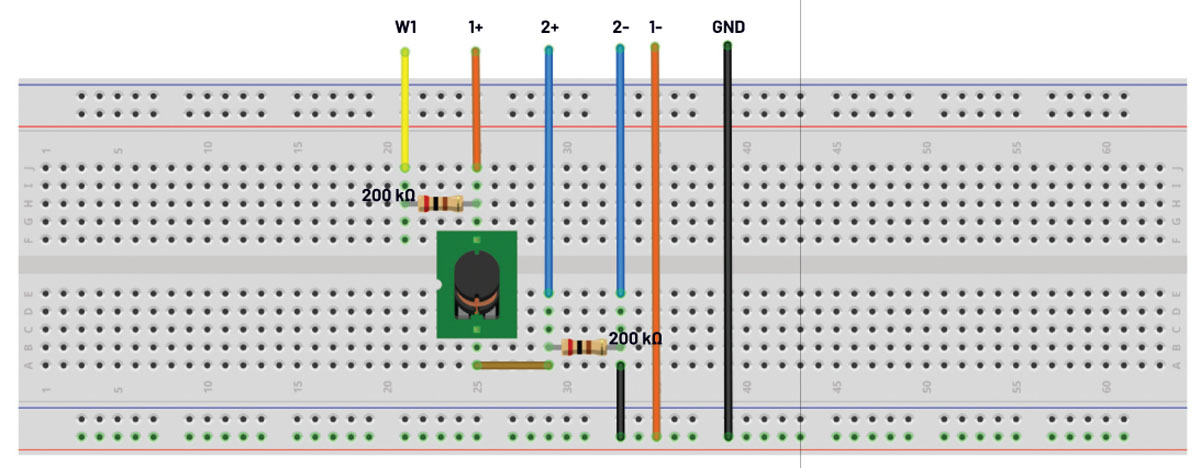
Rys. 5. Schemat połączeń

Konfiguracja sprzętu

Połączenia z wyjściem AWG i wejściami pomiarowymi są oznaczone niebieskimi polami na rys. 4. W trakcie eksperymentu można pojedynczo mierzyć również inne dostępne cewki o różnych indukcyjnościach.

Procedura

Rys. 6. Schemat pomiarowy

Otwórz okno analizatora sieci i skonfiguruj przemiatanie tak, aby rozpoczynało się przy 100 kHz i zatrzymywało przy 20 MHz. Ustaw amplitudę na 5 V, a offset na 0 V. Ustaw zakres analizy Top=-5 dB, Bottom=-55 dB dla wykresu bode. Ustaw offset fazy na 0°, a zakres na 360°. Wybierz jako źródło przebieg z kanału 1. Ustaw liczbę kroków na 1.001k.Wykonaj pojedynczy pomiar. Powinieneś zobaczyć wykresy amplitudy i fazy w funkcji częstotliwości, które wyglądają bardzo podobnie do wyników symulacji. Dane można wyeksportować do pliku .csv w celu dalszej analizy w programie Excel lub MATLAB®.

Rys. 7. Wyniki pomiarów dla RL=200 Ω

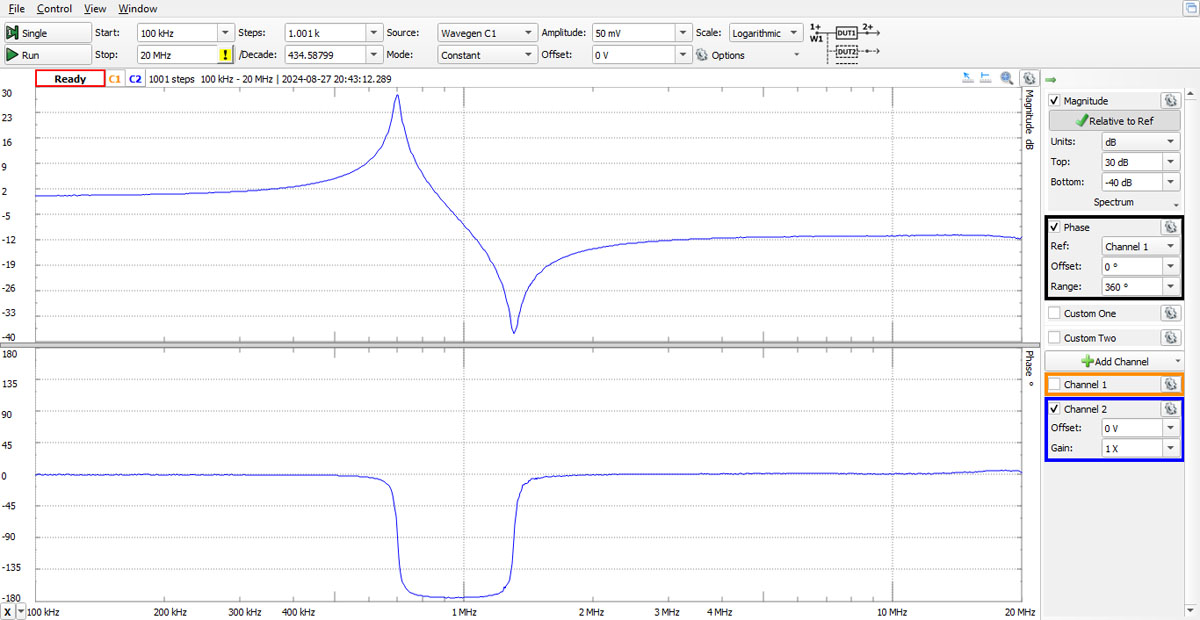
Rys. 8 Wyniki pomiarów dla RL=1 MΩ

Opracowanie Jarosław Doliński na podstawie artykułu „ADALM2000 Activity: Inductor Self Resonance” Antoniu Miclausa i Douga Mercera z Analogue Dialog