Systemy sterowania silnikiem zostały zdominowane przez mikrokontrolery dedykowane, opracowane specjalnie na potrzeby tego typu zastosowań. W wielu przypadkach stosuje się mikrokontrolery z dwoma rdzeniami obliczeniowymi, spośród których jeden wykonuje algorytm sterowania silnikiem, natomiast drugi odpowiedzialny jest za pracę peryferiów (zasobów wewnętrznych) układu.

W artykule opisano w jaki sposób skomplikowany algorytm sterowania silnikiem może zostać w łatwy i bezpośredni sposób zaimplementowany w mikrokontrolerach ogólnego przeznaczenia, wyposażonych w rdzeń ARM Cortex-M4F i zestaw zaawansowanych ( smart ) peryferiów. Takimi mikrokontrolerami są układy XMC4000 firmy Infineon.

Aby posłużyć się przykładem, przedstawione zostaną równania wykorzystywane w metodzie sterowania polowo-zorientowanego (FOC – Field Oriented Control ) użytej na potrzeby sterowania silnikiem PMSM (Permanent Magnet Synchronous Motor ) i pokazane zostanie w jaki sposób mogą one zostać wyliczone przy pomocy biblioteki CMSIS (Cortex Microcontroller Software Interface Standard ) DSP.

Budowa i zasada działania silnika PMSM

Zanim przedstawiony zostanie algorytm FOC, istotne jest zrozumienie budowy i zasady działania silnika PMSM.

Silnik PMSM to silnik z magnesami trwałymi. Prosty 3-fazowy silnik PMSM zbudowany jest z wirnika z magnesami trwałymi oraz stojana z trzema uzwojeniami rozłożonymi sinusoidalnie co 120 stopni. Ze względu na sposób zasilania i sterowania PMSM to silnik synchroniczny. Na rysunku 1 pokazano przekrój silnika PMSM.

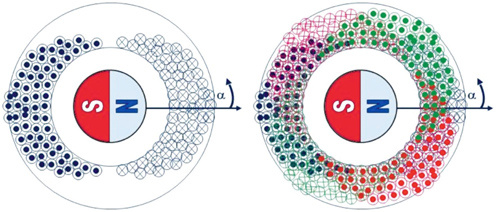
Rys. 1. Przekrój silnika PMSM 2-biegunowego (A) oraz silnika PMSM z trzema uzwojeniami (B). Uzwojenia stojana są rozłożone sinusoidalnie. Symbole kropek i krzyżyków w okręgach symbolizują kierunek uzwojeń

Do zasilania silnika PMSM stosowany jest układ 3-fazowy z przebiegami sinusoidalnymi. Po włączeniu zasilania wytworzony zostanie wirujący strumień magnetyczny. Wartość strumienia jest proporcjonalna do natężenia prądu oraz liczby zwojów uzwojenia. Mnożąc liczbę zwojów przez wartość prądu możliwe jest wyliczenie wartości strumienia. Jest to tak zwana siła magnetomotoryczna (MMF – Magnetomotive Force ). Sumując wartości MMF dla wszystkich trzech faz otrzymać można całkowitą wartość strumienia.

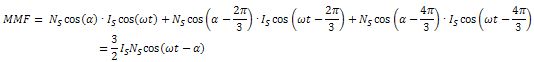
Aby w sposób efektywny sterować silnikiem, należy wytworzyć strumień stojana przesunięty o 90 stopni względem strumienia wirnika. Moment obrotowy silnika jest wtedy proporcjonalny do amplitudy strumienia stojana.

Metoda FOC sterowania silnikiem

Rysunek 2 jest uproszczeniem rysunku 1 (B) uzyskanym poprzez użycie osi i wektorów zamiast okręgów z symbolami kierunku uzwojeń. Prąd płynący w fazie ‘a’ (uzwojenie oznaczone kolorem niebieskim) jest pokazane jako wektor na osi ‘a’ (i _a ). Analogicznie sytuacja występuje dla fazy ‘b’ (uzwojenie zaznaczone kolorem czerwonym) i ‘c’ (uzwojenie zaznaczone kolorem zielonym). Całkowity prąd uzwojeń (i _a + i _b + i _c ) reprezentuje wektor i _s. Celem jest zachowanie kąta 90 stopni pomiędzy is a strumieniem magnetycznym wytworzonym przez magnesy trwałe wirnika. Na rysunku 2 (B) warunek ten jest spełniony, gdy wektor i _s jest zgodny z osią q. Jak pokazuje przykład, występuje pewna niezgodność.

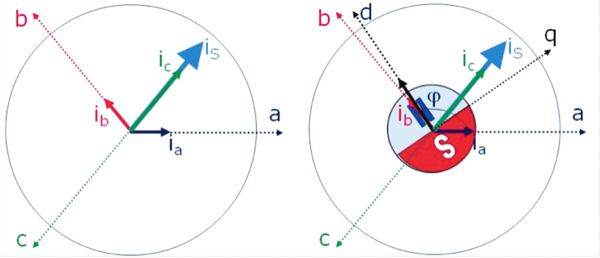
Rys. 2. Wektorowe przedstawienie silnika PMSM pokazujące prądy w trzech fazach (i _a, i _b, i _c ). Na rysunku B zaznaczono dodatkowo strumień magnetyczny (oś d). Dla maksymalnej efektywności i _s musi być zgodne z osią q

Aby uzyskać strumień magnetyczny stojana zgodny z wirnikiem, należy wpierw zidentyfikować parametr strumienia stojana zgodny z wirnikiem. Jest to prąd i _q zaznaczony na osi q. Należy również zidentyfikować parametr strumienia stojana, dla którego występuje niezgodność z wirnikiem. Jest to prąd i _d zaznaczony na osi d.

I _d oraz i _q są rzutem wektora i _s na osie d i q. Pokazano to na rysunku 3.

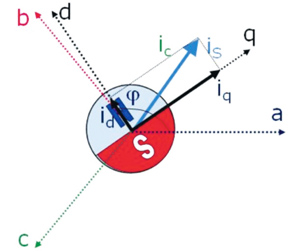
Rys. 3. i _q jest parametrem strumienia stojana wytwarzającym pożądany moment obrotowy. i _d z kolei powinno mieć wartość zero. Wartości i _q i i _d można otrzymać przez wykonanie rzutu i _s na osie q i d

W celu określenia wartości i _d i i _q niezbędne są równania. W celu wyprowadzenia tych równań przydatny okaże się rysunek 4. Prądy stojana i pozycję wirnika można zamienić na i _d oraz i _q w dwóch etapach. Pierwszym etapem jest wykonanie transformacji Clarka ( Clarke Transform ). Transformacja ta przekształca i _a, i _b oraz i _c na i _α oraz i _β, co pokazano na rysunku 4 (A). Drugim etapem jest przekształcenie i _α oraz i _β na i _d oraz i _q. Proces ten jest zwany transformacją Parka ( Park Transform ). W celu samodzielnego wyprowadzenia równań należy wiedzieć, że i _a + i _b + i _c = 0.

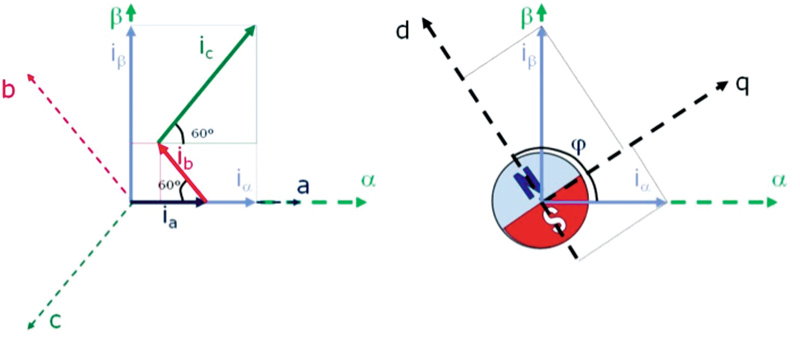
Rys. 4. Graficzna prezentacja transformacji Clarka (A) i Parka (B)