Sygnały kwadraturowe opierają się na liczbach zespolonych i są tematem, który przysparza bardzo dużo problemów młodym adeptom cyfrowego przetwarzania sygnałów. Dzieje się tak właśnie za sprawą otaczającej liczby zespolone terminologii, czyli takich pojęć jak jednostka urojona, liczba zespolona, część rzeczywista czy ortogonalność. Jeśli nie czujesz się pewnie, gdy idzie o fizyczną interpretację liczb zespolonych i jednostki urojonej 
, nie miej sobie tego za złe, bo jesteś w doborowym towarzystwie. Nawet Karol Gauss, jeden z największych matematyków w historii, nazwał liczbę j „cieniem cieni”. W niniejszym artykule spróbujemy rzucić na ten cień nieco światła, żebyś już nigdy nie musiał szukać pomocy w związku z sygnałami kwadraturowymi u szamanów i wróżek.
|
Chcesz być na czasie? Tematyka SDR jest coraz ważniejsza we współczesnej elektronice, poświęciliśmy jej kilka ważnych artykułów, których wykaz jest dostępny pod tym linkiem. |
Przetwarzanie sygnałów kwadraturowych jest używane w wielu dziedzinach nauki i inżynierii, a same te sygnały są niezbędne do opisu przetwarzania i implementacji we współczesnych, cyfrowych systemach komunikacyjnych. W tutorialu omówimy podstawy liczb zespolonych i zaznajomimy się z tym, jak są wykorzystywane do reprezentacji sygnałów kwadraturowych. Następnie przedstawimy pojęcie ujemnej częstotliwości, występujące w algebraicznej notacji sygnałów kwadraturowych i nauczymy się mówić językiem przetwarzania kwadraturowego. Co więcej, wykorzystamy trójwymiarowe wykresy czasowo-częstotliwościowe, aby nadać sygnałom kwadraturowym fizyczną interpretację. Niniejszy artykuł zakończymy natomiast krótkim spojrzeniem na możliwości generacji sygnałów kwadraturowych poprzez tzw. próbkowanie kwadraturowe.
Dlaczego sygnały kwadraturowe w ogóle nas obchodzą?
Sygnały kwadraturowe, nazywane też zespolonymi są wykorzystywane w wielu zastosowaniach, m.in.:
- cyfrowych systemach komunikacyjnych,
- systemach radarowych,
- schematach przetwarzania mających określić różnice czasowe w radionamiernikach,
- systemach mierzących impulsy koherentne,
- układach kształtowania wiązki,
- modulatorach jednowstęgowych, itp.
Wszystkie te zastosowania mieszczą się w ogólnej kategorii tzw. przetwarzania kwadraturowego i wykorzystują koherentne pomiary fazy sygnałów sinusoidalnych.
Sygnał kwadraturowy to sygnał dwuwymiarowy, którego wartość w konkretnym punkcie czasowym można określić za pomocą liczby zespolonej, mającej dwie składowe – część rzeczywistą i urojoną. Używane tradycyjnie słowa „rzeczywisty” i „urojony” są niefortunne, z powodu swoich znaczeń w mowie potocznej. Inżynierowie telekomunikacji często używają tu terminów „składowa w fazie” oraz „składowa kwadraturowa”, ale więcej o tym powiemy później. Teraz natomiast przyjrzyjmy się matematycznej notacji związanej z liczbami zespolonymi.
Rozwój liczb zespolonych i ich notacja
Aby ustalić terminologię, zdefiniujemy liczby rzeczywiste jako te znane z codziennego życia, określające wartość napięcia, temperatury na skali Celsjusza czy stan konta w banku. Te jednowymiarowe liczby mogą być dodatnie lub ujemne, co zostało przedstawione na rysunku 1a. Jest na nim widoczna oś liczbowa, a pojedynczą liczbę rzeczywistą można zobrazować jako punkt na tej osi. Zgodnie z konwencją nazwiemy tę oś osią rzeczywistą.
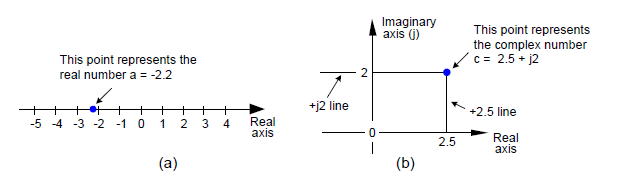
Rys. 1. Graficzna interpretacja liczby rzeczywistej i zespolonej
Liczba zespolona (z ang. complex), oznaczana literą c, jest z kolei przedstawiona na rysunku 1b, również jako punkt. Liczby zespolone nie są ograniczone do jednowymiarowej osi, ale mogą leżeć gdziekolwiek na dwuwymiarowej płaszczyźnie, nazywanej płaszczyzną zespoloną (niektórzy matematycy lubią ją nazywać diagramem Arganda). Płaszczyzna ta pozwala przedstawiać liczby zespolone mające zarówno część rzeczywistą, jak i urojoną. Dla przykładu, na rysunku 1b liczba c = 2,5 + j 2 jest odwzorowana jako punkt leżący na płaszczyźnie zespolonej, ale nie na osi rzeczywistej czy urojonej. Zlokalizujemy punkt c przesuwając się od początku układu współrzędnych o 2,5 jednostki na osi rzeczywistej i o 2 jednostki na osi urojonej. O osiach tych można myśleć tak samo, jak o kierunkach wschód-zachód i północ-południe na mapie.
Wykorzystamy teraz reprezentację geometryczną, aby lepiej zrozumieć część działań arytmetycznych na liczbach zespolonych. Jak widać na rysunku 2, można wykorzystać trygonometrię w trójkącie prostokątnym do zdefiniowania kilku różnych sposobów reprezentacji liczby zespolonej c.
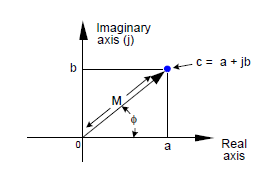
Rys. 2. Reprezentacja wskazowa liczby zespolonej c = a + jb na płaszczyźnie zespolonej
Liczba zespolona c jest w literaturze reprezentowana na kilka różnych sposobów, takich jak:
|
Nazwa notacji |
Wyrażenie matematyczne |
Uwagi |
|
Postać algebraiczna (kanoniczna) |
c = a + jb (1) |
Wykorzystywana do objaśnień, najprostsza do zrozumienia. Nazywana też postacią kartezjańską. |
|
Postać trygonometryczna |
c = M [cos(Φ) + jsin(Φ)] (2) |
Używana powszechnie do opisu sygnałów kwadraturowych w systemach komunikacyjnych. |
|
Postać wykładnicza |
c = Me jΦ (3) |
Najmniej intuicyjna, chociaż najczęściej wykorzystywana w zapisach matematycznych. Czasami zapisywana jako Mexp(jΦ). |
|
Postać moduł-kąt |
c = M ∠ Φ (4) |
Używana do opisów, ale zbyt nieporęczna do wykorzystywania w równaniach. Zasadniczo jest to skrócona forma równania (3). |
Równania (3) i (4) przypominają nam, że liczbę c można interpretować także jako koniec wskazu na płaszczyźnie zespolonej, o długości M i przesunięciu fazowym Φ w stosunku do osi rzeczywistej, jak to przedstawia rysunek 2. Pamiętajmy, że c jest liczbą zespoloną, a wielkości a, b, M i Φ są liczbami rzeczywistymi. Długość wskazu, nazywaną czasem modułem liczby c można wyliczyć ze wzoru:
(5)
