Pytanie dodatkowe: W którym filmie z roku 1939, uważanego przez wielu za najlepszy film w historii, główny bohater próbował przytaczać równanie (5)?

Wróćmy do konkretów. Kąt fazowy Φ, nazywany też argumentem liczby zespolonej jest równy arcus tangensowi stosunku części urojonej do części rzeczywistej lub:

 (6)

Jeśli porównany ze sobą równania (3) i (2), otrzymamy nowy zapis: 

Łatwo uzyskujemy z niego z kolei zapis będący jedną z tożsamości Eulera:

 (7)

Podejrzliwy czytelnik powinien teraz zapytać „Dlaczego można reprezentować liczbę zespoloną używając takiego dziwnego zapisu, wykorzystującego podstawę logarytmu naturalnego e podniesioną do potęgi urojonej?”. Możemy to łatwo wyjaśnić, jak to zrobił największy światowy ekspert od ciągów nieskończonych, pan Leonard Euler, podstawiając j Φ w miejsce zmiennej z w rozwinięciu w szereg funkcji , widocznego w pierwszej linijce rysunku 3. Podstawienie to widać w linijce drugiej. Następnie wyliczamy potęgi jednostki urojonej j, co pokazano w linijce trzeciej. Czytelnicy, którzy mają tak wysokie umiejętności matematyczne, jak Euler (lub ci, którzy sięgną do jakiegoś podręcznika matematyki) rozpoznają, że uzyskanym tak szeregu znajdziemy składniki rozwinięć w szeregi funkcji sinus i kosinus.

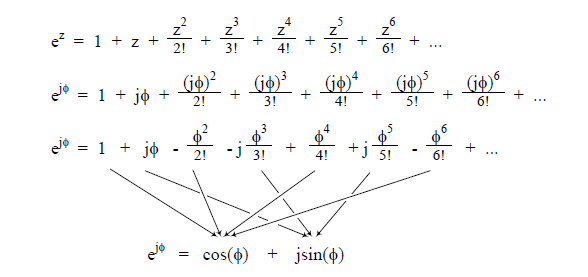
Rys. 3. Jedno z wyprowadzeń tożsamości Eulera z równania (7) z użyciem rozwinięcia w szereg funkcji e^z, cos(Φ) oraz sin(Φ)

Rysunek 3 pozwala zweryfikować równanie (7) oraz reprezentację liczby zespolonej z użyciem równania (3), czyli postaci wykładniczej. Jeśli podstawimy –j Φ w miejsce zmiennej z w pierwszej linijce rysunku 3, uzyskamy nieco inną, również bardzo użyteczną tożsamość Eulera:

 (8)

Wykładnicza forma równań (7) i (8) niesie wiele korzyści:

• Upraszcza operacje matematyczne i analizę:

– przechodzimy z równań trygonometrycznych na prostą algebrę wykładników,

– operacjami matematycznymi na liczbach zespolonych rządzą te same zasady, co przy liczbach rzeczywistych.

• Sprowadza dodawanie sygnałów zespolonych do dodawania liczb zespolonych, czyli sumowania wektorów.
• jest to najbardziej spójna notacja.
• wskazuje na sposób implementacji i opisu cyfrowych systemów telekomunikacyjnych wystepujący w literaturze.

Będziemy używać równań (7) i (8) do pokazania, dlaczego i jak sygnały kwadraturowe są wykorzystywane w cyfrowych systemach komunikacyjnych. Ale najpierw weźmy głęboki oddech i wkroczmy w „strefę cienia” jednostki urojonej j.

Widzieliśmy już definicję: . Jeśli chcielibyśmy wyrazić ją słowami, powiemy że j oznacza liczbę, która pomnożona przez samą siebie da wynik ujemny. Definicja ta sprawia wiele problemów początkującym, gdyż wszyscy mamy intuicję mówiącą, że liczba pomnożona przez samą siebie daje wynik dodatni. Niestety wiele książek dotyczących cyfrowego przetwarzania sygnałów wprowadza definicję j, a następnie, z uzasadnionym pośpiechem, gładko przechodzi do omawiania sposobów jej zastosowania do analiz sygnałowych. Powoduje to, że czytelnicy szybko zapominają, co zapis „ ” oznacza. Pierwiastek z minus jeden jest na matematycznej scenie już od całkiem dawna, ale nie był brany na poważnie, dopóki nie zastosowano go do rozwiązywania równań kwadratowych w szesnastym wieku. [1], [2] Matematycy niechętnie zaczęli akceptować tę abstrakcyjną koncepcję, nawet bez konieczności wizualizowania jej, gdyż własności 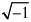 były spójne z arytmetyką liczb rzeczywistych.

Dopiero w osiemnastym wieku wprowadzone przez Eulera porównanie liczb zespolonych do rzeczywistych funkcji sinus i kosinus oraz genialny pomysł Gaussa, który zaproponował płaszczyznę zespoloną, naprawdę uprawomocniły  w europejskiej matematyce. Euler, wychodząc poza domenę liczb rzeczywistych, pokazał że liczby zespolone miały prosty i spójny związek z dobrze znanymi, rzeczywistymi funkcjami trygonometrycznymi. Tak jak Einstein udowodnił równoważność masy i energii, Euler pokazał równoważność rzeczywistych sinusów i kosinusów oraz liczb zespolonych. I tak jak współcześni fizycy nie wiedzą czym jest elektron, ale rozumieją jego własności, my nie będziemy się martwili czym jest j, ale zadowolimy się zrozumieniem jej zachowania. Dla naszych celów, jednostka urojona odpowiada operacji obrotu liczby zespolonej o 90 stopni przeciwnie do ruchu wskazówek zegara. Zobaczmy dlaczego.

Oswoimy się z reprezentacją liczb urojonych na płaszczyźnie zespolonej badając własności jednostki urojonej , zobrazowane na rysunku 4.

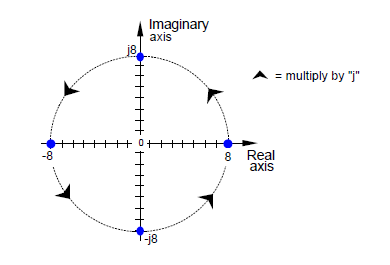
Rys. 4. Co dzieje się z liczbą rzeczywistą 8, gdy zaczynamy mnożyć ją przez jednostkę urojoną.

Przemnożenie dowolnej liczby rzeczywistej przez j skutkuje otrzymaniem urojonego wyniku, który można odłożyć na osi urojonej (pionowej). Przykład z rysunku 4 pokazuje, że jeśli liczbę 8 oznaczymy kropką leżącą na dodatniej części osi rzeczywistej (poziomej), mnożąc ją przez j uzyskamy liczbę urojoną j8, która obrócona została o 90 stopni przeciwnie do ruchu wskazówek zegara. Następne przemnożenie przez j da nam kolejny obrót, skutkujący zatrzymaniem na wartości –8, gdyż . Kolejne mnożenie przez j da nam wartość –j8, leżącą na ujemnej części osi urojonej i tak dalej. Jak łatwo się przekonać, mnożenie przez –j odpowiada z kolei obrotom o 90 stopni w kierunku zgodnym z ruchem wskazówek zegara.

Jeśli za kąt Φ w równaniu (7) podstawimy π/2, możemy zapisać, że:

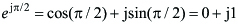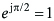 lub  (9)

Mamy więc pierwszy podstawowy fakt wart zapamiętania: jeśli liczbę zespoloną, reprezentowaną jako punkt na płaszczyźnie zespolonej przemnożymy przez j lub , uzyskamy nową liczbę zespoloną, obróconą w stosunku do niej o 90 stopni w kierunku przeciwnym do ruchu wskazówek zegara. Jest to bardzo przydatna wiedza, gdy zaczynamy się zagłębiać w literaturę dotyczącą systemów przetwarzających sygnały kwadraturowe.

Zatrzymajmy się na chwilę, by złapać oddech. Nie przejmuj się, jeśli idee liczb urojonych i płaszczyzny zespolonej wydają się nieco tajemnicze. Na początku jest tak dla wszystkich – koncepcje te staną się bardziej zrozumiałe w miarę używania ich. Pamiętajmy, że jednostka urojona stanowiła zagadkę dla europejskich matematyków największego kalibru przez setki lat. Co więcej, nie tylko sama matematyka stojąca za liczbami zespolonymi jest dosyć dziwna – terminologia, która im towarzyszy też jest nietypowa. Już słowo „urojony” jest niezbyt fortunne, a termin „zespolone” (complex) to już zwyczajne dziwactwo. Gdy się z nim spotykamy, zwłaszcza w języku angielskim, w którym to samo słowo oznacza tyle, co „złożony” lub „trudny”, możemy się poczuć zdeprymowani. A szkoda, bo temat nie jest wcale aż taki skomplikowany. Pamiętajmy tylko, że powodem tych matematycznych wynurzeń była próba uzasadnienia równań (2), (3), (7) i (8). Mając to za sobą, możemy przejść do omówienia zagadnienia sygnałów w dziedzinie czasu.