Reprezentacja sygnałów rzeczywistych z użyciem wskazów zespolonych

Skierujmy teraz naszą uwagę na liczbę zespoloną będącą funkcją czasu. Wyobraźmy sobie liczbę o module (długości wskazu) równym jeden, której kąt fazowy rośnie z czasem. Liczba ta, zaznaczona na rysunku 5a niebieską kropką, to . Człon „ ” oznacza częstotliwość w radianach na sekundę i odpowiada obrotom w tempie f₀ pełnych okręgów na sekundę, gdzie f₀ jest mierzona w hercach. Wraz ze wzrostem wartości czasu t wzrasta kąt fazowy, a nasza liczba orbituje wokół początku układu współrzędnych w kierunku przeciwnym do ruchu wskazówek zegara. Rysunek 5a pokazuje liczbę zatrzymaną w arbitralnie wybranym punkcie czasu, oznaczoną przez niebieską kropkę. Jeśli częstotliwość f₀ byłaby równa powiedzmy 2 Hz, kropka obracałaby się wokół początku układu dwa pełne okręgi na sekundę. Możemy też wyobrazić sobie drugą liczbę zespoloną , oznaczoną na rysunku kropką białą, obracającą się w kierunku zgodnym z ruchem wskazówek zegara, gdyż jej kąt fazowy maleje ze wzrostem wartości czasu.

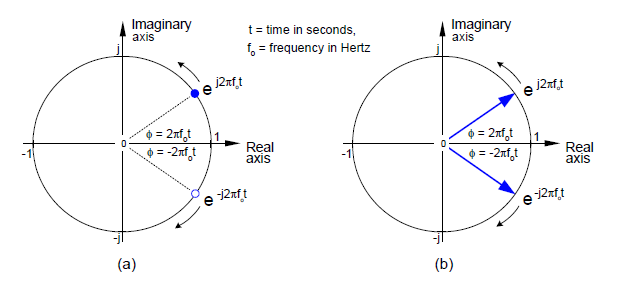
Rys. 5. Dwie liczby zespolone, których potęgi zmieniają się w czasie dla ustalonej chwili czasu

Nazwijmy teraz dwa wyrażenia zespolone  i  sygnałami kwadraturowymi. Oba mają część rzeczywistą oraz urojoną i oba są funkcjami czasu. Wyrażenia te są często nazywane w literaturze liczbami zespolonymi w postaci wykładniczej.

Można też o tych dwóch sygnałach  i  myśleć jako o końcach wskazów, które obracają się w przeciwnych kierunkach, co zobrazowano na rysunku 5b. Na chwilę zostaniemy przy tej interpretacji, bo pozwoli ona osiągnąć cel, jakim jest reprezentacja rzeczywistych sinusoid na płaszczyźnie zespolonej. Nie regulujcie odbiorników!

Aby upewnić się, że rozumiemy zachowanie tych wskazów, na rysunku 6a przedstawiona została w trzech wymiarach ścieżka, jaką pokonuje wskaz  wraz z upływem czasu. Aby pokazać spiralną drogę, po jakiej porusza się wskaz, dodana została oś czasu, skierowana w stronę czytelnika. Rysunek 6b obrazuje za to ciągłą wersję ścieżki, którą pokonuje sam koniec wskazu. Liczba zespolona  lub jeśli wolimy koniec wskazu, porusza się po trajektorii przypominającej korkociąg, okrążającej oś czasu i wyśrodkowanej wokół niej. Rzeczywista i urojona część liczby są przedstawione w postaci rzutów, które mają kształt sinusoidy i kosinusoidy.

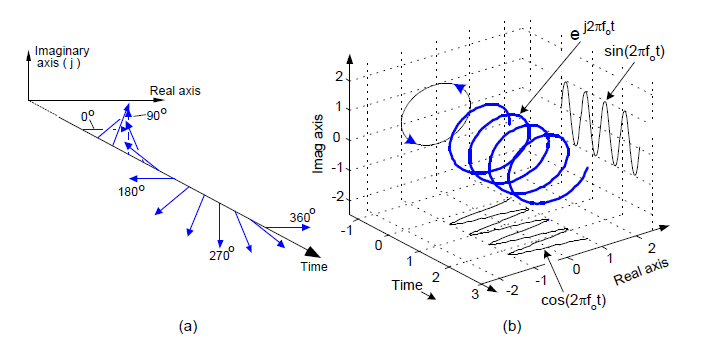
Rys. 6. Ruch wskazu (a) i końca wskazu (b) reprezentującego liczbę 

Powróćmy na chwilę do rysunku 5b i zadajmy sobie pytanie „jaka jest wektorowa suma tych dwóch wskazów, obracających się w przeciwnych kierunkach?”. Części rzeczywiste wskazów będą się sumować, a części urojone znosić. Oznacza to, że suma wskazów 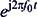 i  zawsze będzie rzeczywista. Właśnie na tej własności opierają się implementacje współczesnych systemów komunikacyjnych!

Aby podkreślić znaczenie faktu, że suma dwóch zespolonych sinusoid jest rzeczywista, narysujmy jeszcze jeden wykres. Rozważmy przebieg w trójwymiarowej przestrzeni przedstawiony na rysunku 7, wygenerowany przez sumę dwóch wskazów zespolonych o połowicznej amplitudzie /2 i /2, poruszających się wzdłuż osi czasu z obrotem wokół niej.

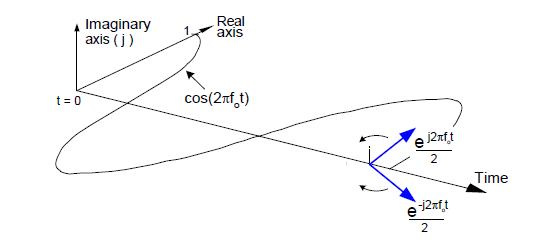
Rys. 7. Kosinusoida reprezentowana przez sumę dwóch wskazów zespolonych

Gdy pomyślimy o tych wskazach, staje się jasne, dlaczego kosinus można przyrównać do sumy dwóch liczb zespolonych w postaci wykładniczej:

  (10)

Równanie (10), dobrze znane i bardzo istotne, także jest jedną z tożsamości Eulera. Mogliśmy do niego dojść rozwiązując układ równań (7) i (8), szukając jsin(Φ), porównując je i rozwiązując tak powstałą równość szukając cos(Φ). Wykonując analogiczne ćwiczenie mogliśmy też pokazać, że rzeczywistą sinusoidę także można przedstawić jako sumę liczb zespolonych w postaci wykładniczej:

 (11)

Przyjrzyjmy się równaniom (10) i (11) uważnie – są to standardowe wzory na sinus i kosinus wykorzystujące notację zespoloną, które często pojawiają się w literaturze dotyczącej kwadraturowych systemów komunikacyjnych. Aby uchronić czytelników przed bólem głowy, zaznaczymy tylko, że jedynym celem rysunków od 5 do 7 jest uzasadnienie wzorów (10) i (11). Te dwa równania, wraz ze wzorami (7) i (8) są dla przetwarzania sygnałów kwadraturowych tym, czym dla zrozumienia pisma egipskiego kamień z Rosetty.

Mamy teraz narzędzia by swobodnie tłumaczyć sinusoidy rzeczywiste na liczby zespolone w postaci wykładniczej i z powrotem. Powtórzmy, poznajemy teraz w jaki sposób sygnały rzeczywiste, które można przesłać za pomocą kabla koncentrycznego czy zdigitalizować i zapisać w pamięci komputera są reprezentowane w notacji zespolonej. I chociaż prawdą jest, że każda z części liczby zespolonej jest w istocie wyrażana jako liczba rzeczywista, to części te traktujemy nieco inaczej, bo są one w kwadraturze.