Mikrokontroler.pl - portal dla elektroników

Przykład próbkowania kwadraturowego

To czego nauczyliśmy się do tej pory o sygnałach kwadraturowych można wykorzystać poznając proces tzw. próbkowania kwadraturowego. Jest to proces dyskretyzacji w czasie ciągłego (analogowego) sygnału o ograniczonym pasmie i przesuwania jego widma tak, by było wyśrodkowane wokół zera. Zobaczmy, jak działa ten popularny zabieg na przykładzie sygnału ciągłego o pasmie B i częstotliwości środkowej f_c.

 

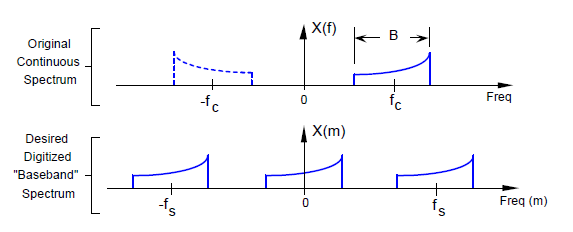
Rys. 13. Widma sygnału przed i po próbkowaniu kwadraturowym

 

Naszym celem w próbkowaniu kwadraturowym jest uzyskanie zdyskretyzowanej w czasie wersji sygnału analogowego o ograniczonym pasmie, ale chcemy też, by widmo tego sygnału miało środek na częstotliwości 0 Hz, a nie f_c. Musimy więc zmieszać sygnał cyfrowy z sygnałem , by dokonać zespolonego przesunięcia częstotliwości. Częstotliwość próbkowania układu dokonującego dyskretyzacji, wyrażaną w próbkach na sekundę oznaczymy f_s. W dolnej części rysunku 13 przedstawiono widma powielone regularnie, by przypomnieć, że taki efekt występuje zawsze przy próbkowaniu.

Przyjrzyjmy się teraz schematowi próbkowania kwadraturowego przedstawionemu w górnej części rysunku 14. Jest on znany jako demodulacja I/Q lub demodulacja Weavera (dla tych, którzy mają doświadczenie z teorią telekomunikacji). Układ dwóch oscylatorów sinusoidalnych przesuniętych względem siebie w fazie o 90 stopni jest często nazywany oscylatorem kwadraturowym.

Składowe  i , przedstawione na rysunku 14 przypominają nam, że tworzące rzeczywistą kosinusoidę składniki zespolone w postaci wykładniczej duplikują każdą z części widma X_bp (f ), by utworzyć widmo X_i (f ). Rysunek pokazuje, jak otrzymujemy odfiltrowaną ciągłą część zespolonego sygnału kwadraturowego będącą w fazie. Widma X_i (f ) i I (f ) są z definicji traktowane, jakby były czysto rzeczywiste.

 

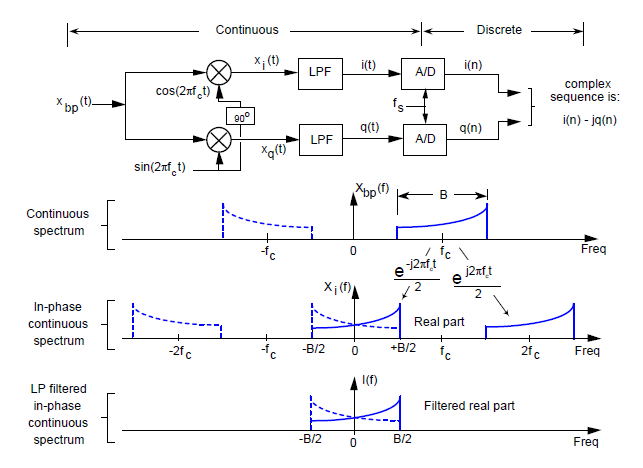
Rys. 14. Schemat blokowy układu realizującego próbkowanie kwadraturowe oraz widma sygnałów w fazie (w górnej gałęzi)

 

Analogiczny rysunek 15 obrazuje, jak poprzez mieszanie sygnałów x_bp (t ) i sin(2πf_c t ) odfiltrowywana jest ciągła część zespolonego sygnału kwadraturowego będącą w kwadraturze.

 

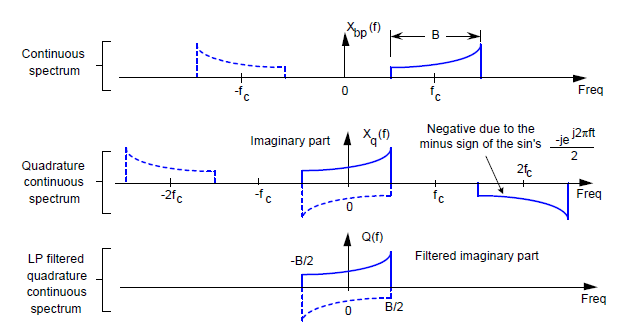
Rys. 15. Widma sygnałów w kwadraturze (w dolnej gałęzi)

 

Dokąd zmierzamy? I(f ) – jQ (f ) to widmo zespolonej repliki naszego pierwotnego sygnału x_bp (t ). Sumowanie tych dwóch widm przedstawia rysunek 16.

 

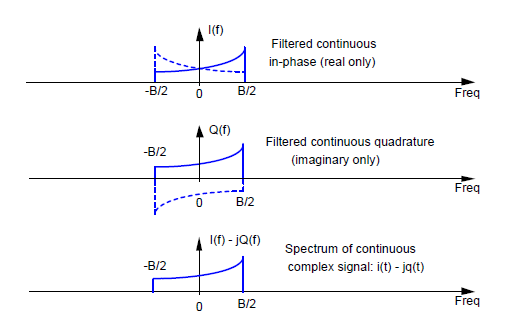
Rys. 16. Łączenie widm I(f) i Q(f), aby uzyskać pożądane widmo I(f) – jQ(t)

 

Typowe zobrazowanie próbkowania kwadraturowego wydaje się niejasne, dopóki nie spojrzymy na nie w trzech wymiarach, co przedstawia rysunek 17, na którym czynnik –j obraca czysto urojone widmo Q (f ) o –90 stopni i czyni je rzeczywistym. Uzyskane widmo –jQ (f ) jest następnie dodawane do I (f ).

 

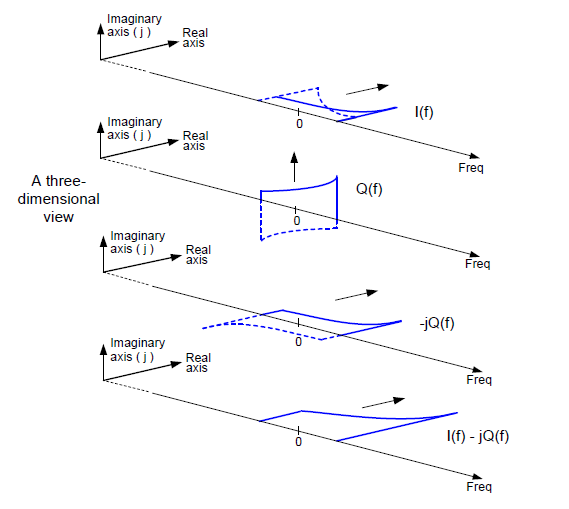
Rys. 17. Trójwymiarowe przedstawienie sumowania widm I (f ) i Q (f ), aby uzyskać widmo I (f ) – jQ (t )

 

Zespolone widmo przedstawione w dolnej części rysunku 18 pokazuje, do czego dążyliśmy – cyfrowa postać zespolonego sygnału wąskopasmowego skupiona wokół częstotliwości 0 Hz.

 

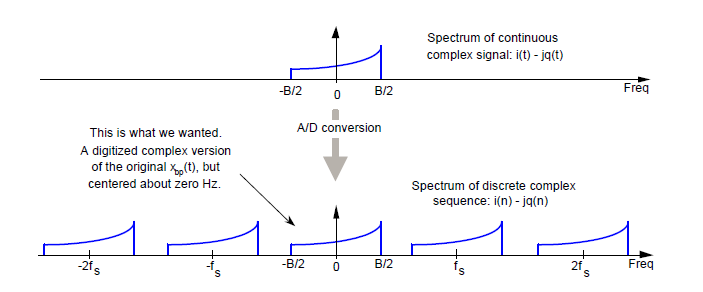
Rys. 18. Zespolony sygnał i (t ) – q (t ) jest poddawany próbkowaniu, aby uzyskać dyskretny sygnał i (n ) – jq (n )

 

Wymieńmy zalety próbkowania kwadraturowego:

• Każdy przetwornik A/C pracuje z częstotliwością o połowę mniejszą, niż przy typowym próbkowaniu rzeczywistym.
• W wielu implementacjach sprzętowych praca z niższym taktowaniem pozwala zaoszczędzić energię.
• Dla danej częstotliwości próbkowania możemy próbkować sygnały o szerszym paśmie.
• Kwadraturowe sekwencje pozwalają na bardziej wydajne przetwarzanie FFT dzięki pokrywaniu szerszego zakresu częstotliwości.
• Jako, że sekwencje kwadraturowe są dwukrotnie nadpróbkowane, możliwa jest realizacja operacji podnoszenia do kwadratu bez konieczności stosowania interpolacji przez upsampling.
• Znajomość fazy sygnałów pozwala na koherentne przetwarzanie.
• Próbkowanie kwadraturowe ułatwia pomiary chwilowej amplitudy i fazy sygnału podczas demodulacji.

Powrót do schematu blokowego przypomina nam ważną cechę sygnałów kwadraturowych. Można przesłać analogowy sygnał kwadraturowy, wykorzystując choćby dwa kable koncentryczne, którymi transmitujemy dwa sygnały rzeczywiste i(t) i q(t). By przesłać sygnał kwadraturowy zdyskretyzowany w czasie potrzebne są dwa wielożyłowe kable, co obrazuje rysunek 19.

 

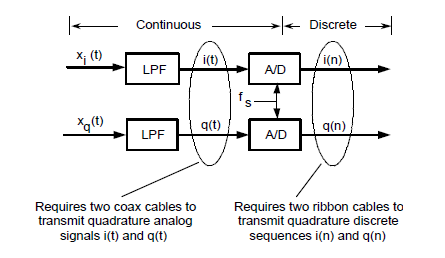
Rys. 19. Kolejne przedstawienie faktu, że sygnały kwadraturowe składają się z dwóch części rzeczywistych

 

Aby docenić fizyczne znaczenie całego tego wywodu, pamiętajmy że ciągły sygnał kwadraturowy x_c (t ) = i (t ) + jq (t ) nie jest tylko matematyczną abstrakcją. Można go wygenerować w laboratorium i przesłać do pomieszczenia w drugim końcu korytarza. Wszystko, czego potrzebujemy to dwa generatory sinusoidalne o tej samej częstotliwości f₀. Musimy też zapewnić synchronizację faz tak, by przesunięcie między nimi stale wynosiło 90 stopni. Następnie podłączamy dwa kable koncentryczne do wyjść generatorów i doprowadzamy ich końce, oznaczone odpowiednio „i (t )” dla sygnału sinusoidalnego i „q (t )” dla kosinusoidalnego do pomieszczenia docelowego.

Teraz krótki, dwupytaniowy quiz. Co zobaczymy na ekranie oscyloskopu, gdy podłączymy dwa ciągłe sygnały i (t ) i q (t ) do wejść X i Y (pamiętając oczywiście, żeby ustawić przemiatanie poziome na źródło zewnętrzne)?

 

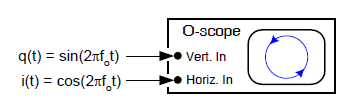
Rys. 20. Wyświetlanie sygnału kwadraturowego z użyciem oscyloskopu

 

Co stałoby się natomiast, gdybyśmy źle oznaczyli kable i podłączyli kanały odwrotnie? Odpowiedź na pierwsze pytanie brzmi: „Zobaczymy plamkę obracającą się w kółko w kierunku przeciwnym do ruchu wskazówek zegara.” Jeśli kable zamienimy miejscami, także zobaczymy plamkę, ale obracającą się zgodnie z ruchem wskazówek zegara. Byłaby to ciekawa demonstracja, gdybyśmy ustawili częstotliwość generatorów na niską wartość, np. 1 Hz.

Przykład z oscyloskopem odpowiada na ważne pytanie: „Jak sprzętowo implementowana jest jednostka urojona, gdy pracujemy z sygnałami kwadraturowymi?”. Odpowiedź na nie brzmi: „Jednostka urojona jest implementowana poprzez odpowiednie traktowanie sygnałów względem siebie.” Musimy podejść do nich ortogonalnie, czyli tak, by sygnał i (t ) odpowiadał zmianie w poziomie, a sygnał w kwadraturze – zmianie w pionie. Ortogonalność oznacza tu, że kierunek pionowy jest przesunięty o 90 stopni w stosunku do poziomu. W przykładzie z oscyloskopem jednostka urojona jest implementowana po prostu poprzez odpowiednie podłączenie sygnałów do wejść. Sygnał w fazie i (t ) steruje odchyleniem w poziomie, a sygnał w kwadraturze steruje odchyleniem w pionie. Wynikiem jest dwuwymiarowy sygnał kwadraturowy, reprezentowany przez położenie plamki na wyświetlaczu.

Osoba siedząca w drugim pomieszczeniu, która odbiera dyskretne sekwencje i (n ) oraz q (n ) może zmieniać orientację finalnego widma zespolonego dodając lub odejmując sekwencję jq (n ), co obrazuje rysunek 21.

 

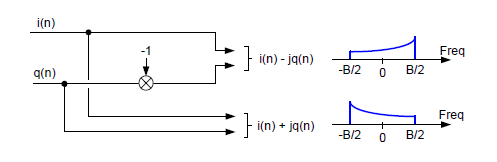
Rys. 21. Zastosowanie zmian znaku sygnału q (n ) do zmiany orientacji widma

 

Górna gałąź z rysunku 21 odpowiada mnożeniu oryginalnego sygnału x_bp (t ) przez , a dolna gałąź – mnożeniu x_bp (t ) przez . A zatem, gdyby składowa kwadraturowa naszego sygnału była ujemna, czyli miała postać –sin(2πf_ct ), wynikowe widmo sygnału zespolonego byłoby odwrócone względem częstotliwości 0 Hz, w stosunku do widm z rysunku 21.

Gdy rozważamy odwracanie widm sygnałów zespolonych, przypomnijmy sobie jeszcze raz, że są dwa proste sposoby na odwrócenie widma amplitudowego sekwencji x(t ) = i (t ) + jq (t ). Po pierwsze, jak przedstawiono na rysunku 21, możemy dokonać sprzężenia, by uzyskać sekwencję x’(t ) = i (t ) + jq (t ). Drugi sposób, to zamiana przebiegów składowych i zastosowanie sekwencji y(t ) = q (t ) + ji (t ). Obie te sekwencje mają takie same widma amplitudowe, odwrotne w stosunku do widma sygnału x(t ), ale ich widma fazowe nie są takie same.

 

Podsumowanie

W tym miejscu zakończymy to wprowadzenie. Nauczyliśmy się, że użycie płaszczyzny zespolonej pozwala zwizualizować matematyczny opis liczb zespolonych oraz zrozumieć związki między sygnałami kwadraturowymi i rzeczywistymi. Zobaczyliśmy też, jak trójwymiarowe wykresy w dziedzinie częstotliwości pomagają zrozumieć procesy generacji sygnałów kwadraturowych oraz ich łączenia i rozkładu. Na koniec przyjrzeliśmy się przykładowi próbkowania kwadraturowego i dwóm sposobom odwracania widma sekwencji kwadraturowej.

 

Bibliografia

[1] D. Struik, A Concise History of Mathematics, Dover Publications, Nowy Jork, 1967.

[2] D. Bergamini, Mathematics, Life Science Library, Time Inc., Nowy Jork, 1963.

[3] N. Boutin, “Complex Signals”, RF Design, Grudzień 1989

Odpowiedź na zagadkę, która pojawiła się po równaniu (5): powiedział tak strach na wróble w filmie „Czarnoksiężnik z krainy Oz”.