[PRZYKŁAD] Obsługa czujnika poziomu cieczy na sterowniku SIMATIC S7-1200 i zestawie symulacyjnym KA-S71200-IO-Simulator
Prezentujemy przykład obsługi czujnika poziomu cieczy na sterowniku przemysłowym Siemens SIMATIC S7-1200. Jako sensor posłuży czujnik 5″ eTape Liquid Level Sensor z oferty Milone Technologies. Wygodne połączenie elementów zapewni zestaw symulacyjny KA-S71200-IO-Simulator produkowany przez Kamami.
Sterownik SIMATIC S7-1200
Produkty Siemens z serii SIMATIC S7-1200 to programowalne sterowniki logiczne (PLC) przeznaczone do małych i średnich aplikacji. Wraz z urządzeniami towarzyszącymi stanowią kompletny system sterowania dla automatyki. Seria, oprócz jednostek centralnych, obejmuje również moduły wejść oraz wyjść cyfrowych i analogowych, moduły komunikacyjne, a także panele HMI. Dzięki implementacji standardowych protokołów komunikacyjnych możliwa jest łatwa integracja sterowników z istniejącymi systemami.
Używany w projekcie sterownik 6ES7211-1AE40-0XB0 cechuje się następującymi właściwościami:
- 6 wejść cyfrowych 24 V DC,
- 4 wyjścia cyfrowe 24 V DC,
- 2 wejścia analogowe od 0 do 10 V DC, rozdzielczość 10 bitów,
- Pamięć: 50 kB,
- Regulator PID z auto tuningiem,
- Zintegrowany ETHERNET – PROFINET,
- Montaż na szynie DIN,
- Zasilanie: 24 V DC,
- Wymiary: 90 x 100 x 75 mm,
- Waga: 370 g.
 Rys. 1. Sterownik PLC SIMATIC S7-1200
Rys. 1. Sterownik PLC SIMATIC S7-1200
Zestaw symulacyjny KA-S71200-IO-Simulator
KA-S71200-IO-Simulator z oferty sklepu Kamami.pl to kompletny zestaw symulujący typowe otoczenie sterownika PLC. Umożliwia on podanie na wejścia cyfrowe i analogowe odpowiednich sygnałów – zarówno z przełączników, jak i wbudowanych czujników, a także zewnętrznych sensorów. Z kolei stan wyjść można odczytać za pomocą diod LED na płytce wyjściowej.
 Rys. 2. Zestaw KA-S71200-IO-Simulator
Rys. 2. Zestaw KA-S71200-IO-Simulator
Kompletny opis zestawu symulacyjnego KA-S71200-IO-Simulator znajdziesz w artykule KA-S71200-IO-Simulator – zestaw symulacyjny dla sterowników SIMATIC S7-1200
Czujnik poziomu cieczy 5” eTape
W roli sensora poziomu cieczy wykorzystamy czujnik eTape firmy Milone Technologies. Ten półprzewodnikowy sensor dysponuje wyjściem rezystancyjnym, którego rezystancja zmienia się wraz z wykrywanym poziomem cieczy. Stosunek ten jest odwrotnie proporcjonalny – wraz ze wzrostem poziomu cieczy rezystancja spada i na odwrót.
Jednak przetworniki analogowo-cyfrowe nie mierzą rezystancji, a napięcie. Oznacza to, że za czujnikiem trzeba umieścić układ konwertujący te wielkości. Najprostszym układem pomiarowym może być klasyczny dzielnik napięciowy. Działa on w następujący sposób – napięcie wejściowe jest dzielone pomiędzy dwa rezystory, a sygnał pomiędzy rezystorami zależy od stosunku rezystancji. Jeśli jedna z rezystancji jest zmienna, a druga stała to napięcie wyjściowe zależy od aktualnej wartości rezystancji zmiennej. Znając wzory łączące zależności w dzielniku, można ze zmierzonego napięcia obliczyć zmieniającą się rezystancję – w tym przypadku czujnika poziomu cieczy.
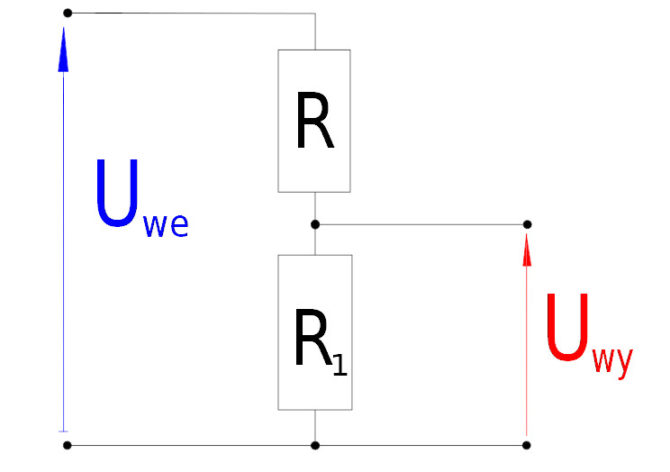 Rys. 3. Schemat dzielnika napięciowego (źródło: wikipedia.org)
Rys. 3. Schemat dzielnika napięciowego (źródło: wikipedia.org)
Zgodnie z dokumentacją spadek rezystancji w funkcji wzrostu poziomu cieczy jest w przybliżeniu liniowy. Oznacza to, że jeśli już obliczymy rezystancję czujnika, to dalsze obliczenia mające na celu wyznaczenie wysokości słupa cieczy są już bardzo proste. Patrząc na charakterystykę sensora warto zwrócić uwagę na tzw. martwą strefę o wysokości 1 cala. Oznacza to, że sensor zaczyna reagować dopiero, gdy poziom cieczy przekracza tą wysokość i dopiero wtedy można mówić o poprawnym pomiarze.
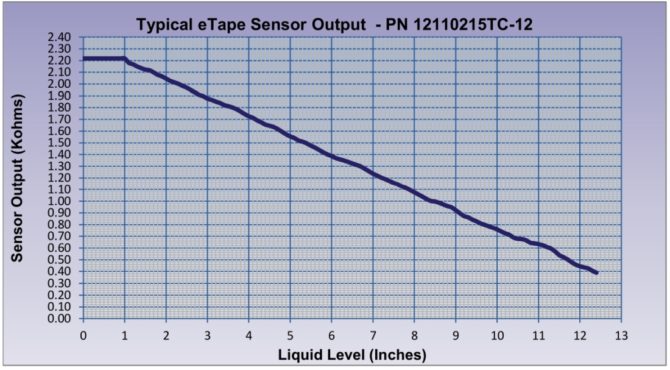 Rys. 4. Charakterystyka sensora eTape
Rys. 4. Charakterystyka sensora eTape
Czujniki poziomu cieczy eTape są dostępne w różnych wymiarach – standardowo 5”, 8” i 12”, a na zamówienie nawet do 70”. Do projektu wykorzystałem sensor o długości 5” umieszczony w eleganckiej obudowie ochronnej. Obudowa ta pozwala na ochronę dość giętkiego i podatnego na uszkodzenie sensora, zawiera układ elektroniczny, w tym stały rezystor referencyjny oraz pozwala wyprowadzić styki czujnika na wygodny, trójżyłowy przewód o długości ok. 30 cm.
 Rys. 5. Czujnik poziomu cieczy 5″ eTape w obudowie
Rys. 5. Czujnik poziomu cieczy 5″ eTape w obudowie
Obsługa czujnika poziomu cieczy eTape
Według dokumentacji, czujniki eTape o długości 5” mają zakres rezystancji 400-1000 Ω i gradient rezystancji 150 Ω/cal (60 Ω/cm). Z kolei obudowa zawiera rezystor referencyjny o wartości 1000 Ω. Problem jest jednak taki, że wszystkie te wartości podano z tolerancją aż 20%. Najlepiej więc sprawdzić samodzielnie jak wyglądają te wartości w konkretnym, zakupionym egzemplarzu. Zmierzyłem więc omomierzem wartości rezystancji od strony zasilania i masy w dwóch przypadkach: przy pustym naczyniu oraz przy naczyniu pełnym (gdy poziom cieczy ma ~5 cali). Oto wyniki
Naczynie puste:
RTOP = 993 Ω
RBOTTOM = 1057 Ω
Naczynie pełne:
RTOP = 404 Ω
RBOTTOM = 1044 Ω
Warto zauważyć tu kilka rzeczy. Po pierwsze, wbrew intuicji, sensor zamontowano od strony zasilania. Nie wiem czy to cecha akurat tego egzemplarza, czy też jest tak we wszystkich sensorach z serii. Po drugie rezystancja referencyjna również nie jest do końca stała, lecz podlega pewnym fluktuacjom. Mimo wszystko są to jednak niewielkie wahania (ok. 1%), więc dla uproszczenia pominę ten efekt i założę, że jest to wartość stała, równa 1050 Ω.
Gradient rezystancji tego egzemplarza wynosi -147,25 Ω/cal (w zakresie od 1 do 5 cali). W przeliczeniu na centymetry jest to ok. 58 Ω/cm.
Przeliczenie napięcia na rezystancję sensora
Jeśli mamy już zmierzone napięcie z dzielnika, to znając zależności występujące w dzielniku napięcia możemy wyprowadzić wzór i obliczyć aktualną rezystancję czujnika. Wiemy, że napięcie z dzielnika jest równe:
Po przekształceniu otrzymujemy wzór na obliczenie rezystancji sensora (od strony zasilania):
Ten wzór zaimplementuję w kodzie programu.
Przeliczenie rezystancji na wysokość słupa cieczy
Aby z otrzymanej rezystancji obliczyć poziom cieczy w naczyniu, należy aktualną rezystancję odjąć od rezystancji przy pustym naczyniu i podzielić przez gradient sensora. Trzeba też pamiętać, że czujnik zaczyna reagować dopiero od wysokości 1 cal, a więc do wyniku należy dodać tą wartość. Wzór na poziom cieczy wynosi więc:
Powyższy wzór pozwala na obliczenie wysokości w calach. Aby otrzymać wysokość w centymetrach należy wynik pomnożyć razy 2,54 (lub też przeliczyć stałe we wzorze).
To już wszystko od strony teoretycznej. Przejdźmy teraz do praktyki.






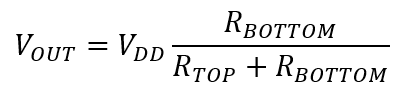
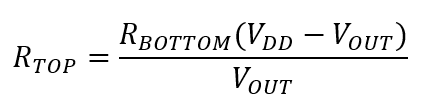
 Nie ma rzeczy niemożliwych: polska elektronika na ISS
Nie ma rzeczy niemożliwych: polska elektronika na ISS  NanoIC otwiera dostęp do pierwszych w historii hybrydowych połączeń między-układowych; zestaw do projektowania (PDK) połączeń typu RDL i D2W
NanoIC otwiera dostęp do pierwszych w historii hybrydowych połączeń między-układowych; zestaw do projektowania (PDK) połączeń typu RDL i D2W  Caroline Pannier – nowa dyrektorka targów electronica – analizuje sytuację gospodarczą branży i przedstawia wyniki
Caroline Pannier – nowa dyrektorka targów electronica – analizuje sytuację gospodarczą branży i przedstawia wyniki 







