Obliczenie FFT na mikrokontrolerze STM32 (1) – Biblioteka CMSIS, wyciek widma, okna wykorzystywane do FFT, wdrożenie w projekcie
Zapraszamy do przeczytania pierwszego z serii artykułów technicznych, których autorami będą współpracujący z nami inżynierowie Mateusz Pluta i Dominik Bednarski. Na rozgrzewkę Mateusz zaproponował obliczenie FFT (Fast Fourier Transform) z przebiegów prądu i napięcia, zebranych za pomocą przetworników ADC, na procesorze STM32.
Więcej artykułów na Blog IntHou
FFT (Fast Fourier Transform):
Myślę, że nie będę opisywał teorii szybkiej transformaty Fouriera, ponieważ wiele materiałów znajdziecie w książkach związanych z przetwarzaniem sygnałów czy w internecie. Moim zdaniem świetnie opisuje FFT grafika z Rys. 1.
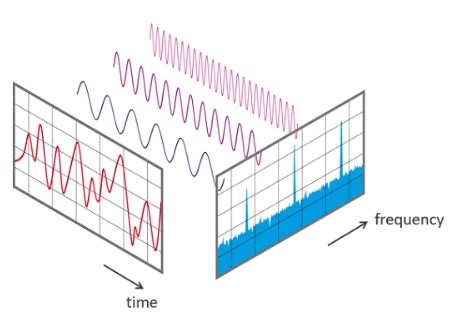
Rys. 1. Sygnał w dziedzinie czasu i częstotliwości [1]
Biblioteka CMSIS:
Do obliczenia FFT użyję biblioteki CMSIS [2], która ma wiele funkcji matematycznych, także związanych z cyfrowym przetwarzaniem sygnałów, między innymi FFT. W bibliotece znajdziecie funkcje do rzeczywistej transformaty Fouriera (RFFT – Real FFT) jak i urojonej (CFFT – Complex FFT). Transformata rzeczywista może być używana tylko do danych rzeczywistych, natomiast transformata urojona do danych urojonych, jak i rzeczywistych. Jeśli dane wejściowe są rzeczywiste to lepiej jest użyć RFFT, ponieważ obliczenia zostaną szybciej wykonane, w porównaniu do transformaty urojonej [3].
Dane wejściowe do funkcji FFT mogą być różnego typu:
- float16_t,
- float32_t,
- float64_t,
- q15,
- q31.
Do obliczenia FFT w swoim projekcie wykorzystałem rzeczywistą transformatę Fouriera, a z biblioteki CMSIS użyłem następujących funkcji:
- arm_rfft_fast_instance_f32 fft_handler – inicjalizacja struktury instancji,
- arm_rfft_fast_init_f32(&fft_handler, fftSize) – inicjalizacja oraz podanie ilości próbek, z których będzie obliczane FFT,
- arm_rfft_fast_f32(&fft_handler, Input_Buffer, Output_Buffer, ifftFlag) – jest to funkcja, która oblicza FFT z danych znajdujących się w buforze wejściowym, zapisując wyznaczony rozkład Fouriera w buforze wyjściowym. Parametr ifftFlag podajemy w celu zdefiniowania czy chcemy wykonać transformatę Fouriera (ifftFlag=0) czy odwrotną transformatę Fouriera (ifftFlag=1). Bufor wyjściowy składa się z części rzeczywistej, jak i urojonej obliczonych dla każdej częstotliwości. Bufor wyjściowy wygląda następująco:
Bufor wyjściowy wygląda tak, ponieważ w dziedzinie częstotliwości druga połowa bufora wyjściowego wygląda tak samo, lecz jest odwrócona w częstotliwości. Zerowy element bufora wyjściowego reprezentuje offset DC, pierwszy element – częstotliwość fundamentalną, drugi element – pierwszą harmoniczną itd. Ważną kwestią jest to, że funkcja arm_rfft_fast_f32() modyfikuje bufor wejściowy, więc jeśli chciałbyś podejrzeć bufor wejściowy po wykonaniu FFT, stwórz dwa identyczne bufory jeden służący do obliczenia FFT, a drugi do obejrzenia sygnału wejściowego.
- arm_cmplx_mag_f32(Output_Buffer, Mag_Output_Buffer, fftSize/2) – jest to funkcja wykonująca moduł z bufora wyjściowego. W celu sprawdzenia energii, jaka występuje w każdym prążku, należy obliczyć moduł z części rzeczywistej, jak i urojonej dla każdej częstotliwości. Moduł z bufora danych wyjściowych wygląda następująco:
- arm_max_f32(Mag_Output_Buffer, fftSize/2, &Max_Mag_Value, &Max_Mag_Value_Index) – jest to funkcja, która wyznacza wartość maksymalną. Dzięki niej wyznaczymy prążek o największej energii.
Częstotliwość próbkowania:
Podczas wykonywania FFT bardzo ważnym elementem jest dobór odpowiedniej częstotliwości próbkowania przetwornika ADC. Częstotliwość próbkowania ma bezpośredni wpływ na dokładność obliczenia FFT, a konkretnie na wyciek widma (spectral leakage).
Wyciek widma jest to zjawisko, kiedy energia z głównej częstotliwości sygnału wycieka do sąsiadujących prążków, świetnie obrazuje to grafika z Rys. 2. Wyciek występuje, kiedy w buforze wejściowym do FFT nie ma całkowitej ilości okresów przebiegu, czyli przebieg traci swą okresowość. Energia z jednej częstotliwości wycieka do sąsiednich prążków. Częstotliwość próbkowania musi wynosić 2^n pomnożone przez częstotliwość mierzonego sygnału. W moim projekcie częstotliwość sygnału pomiarowego będzie wynosiła 5 kHz, 10 kHz lub 20 kHz, więc dobrałem częstotliwość próbkowania 80 kHz. Przy dobranej częstotliwości próbkowania 80 kHz i 256 próbkach, harmoniczne będą rozmieszczone co 312,5 Hz [4], [5].
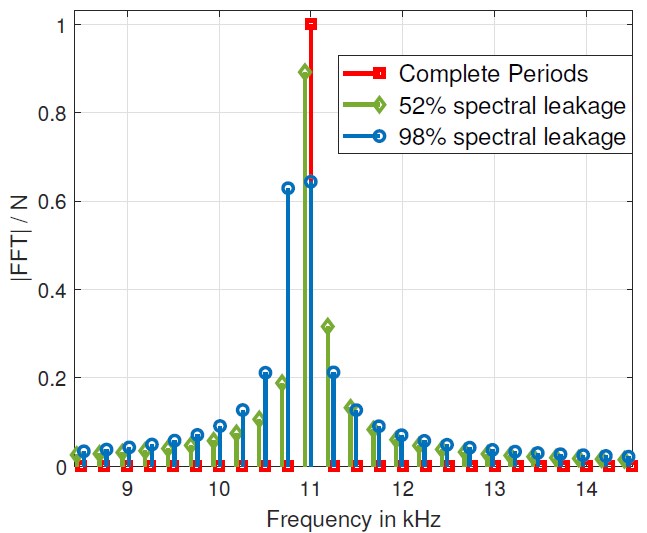
Rys. 2. Wyciek widma [4]

Okna:
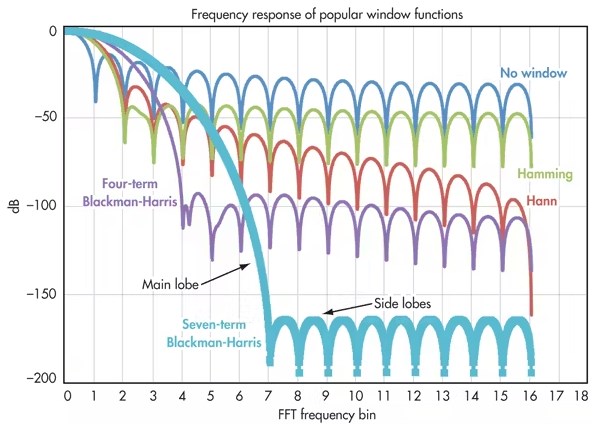
W projektach, gdzie nie jest możliwe spełnienie powyższego kryterium o 2^n liczbie okresów, należy zastosować okna. Okna redukują sygnał do zera na końcach bufora wejściowego do FFT, co finalnie zmniejsza wyciek widma. Wybór odpowiedniego okna zależy od tego, co chcemy osiągnąć, czy zależy nam na fundamentalnym prążku częstotliwości, czy chcemy zobaczyć także pozostałe prążki. Wybór odpowiedniego okna świetnie został opisany w następujących pozycjach: [6], [7].
Podczas realizacji mojego projektu, gdzie kryterium o częstotliwości próbkowania było spełnione, okna inne niż prostokątne wprowadzały wyciek widma. Finalnie wybrałem okno prostokątne.
- Okno Blackmana-Harrisa o równaniu [8]:
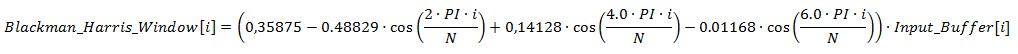
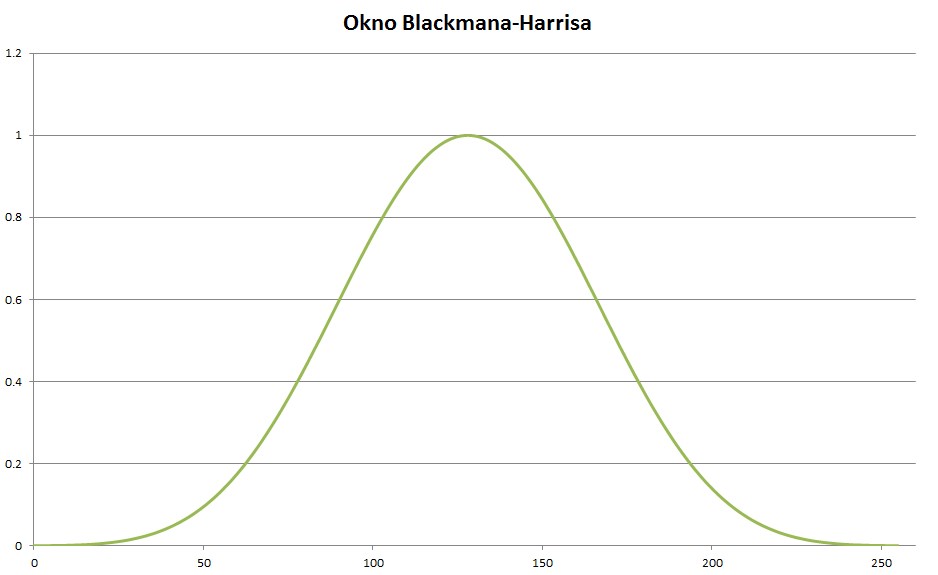 Rys. 4. Okno Blackmana-Harrisa
Rys. 4. Okno Blackmana-Harrisa
Sygnał sinusoidalny przemnożony przez okno Blackmana-Harrisa:
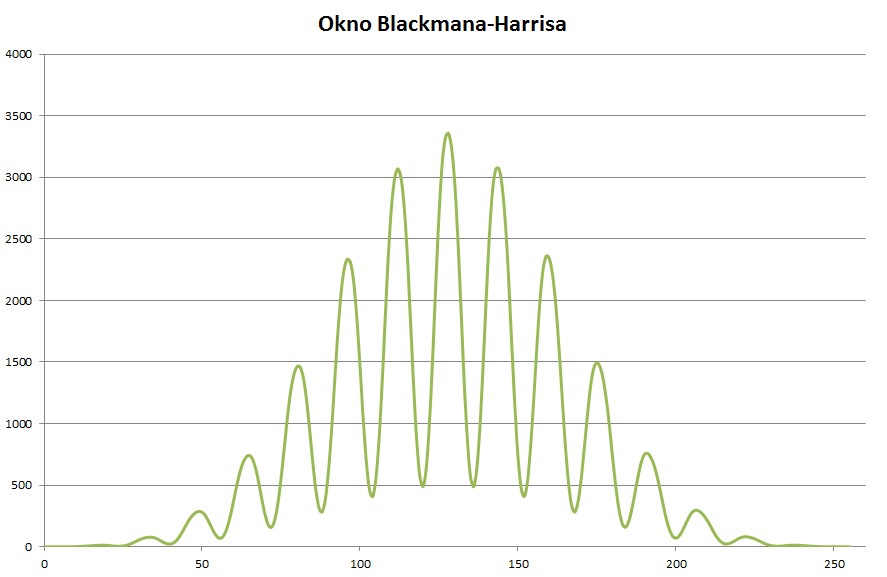
Rys. 5. Sygnał sinusoidalny przemnożony przez okno Blackmana-Harrisa
- Okno Hanninga o równaniu [9]:

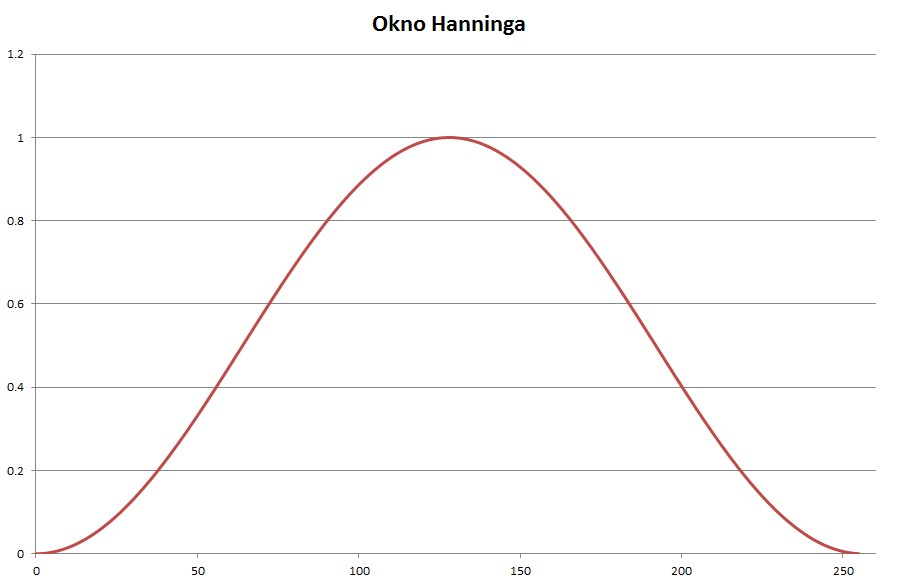
Rys. 6. Okno Hanninga
Sygnał sinusoidalny przemnożony przez okno Hanninga:
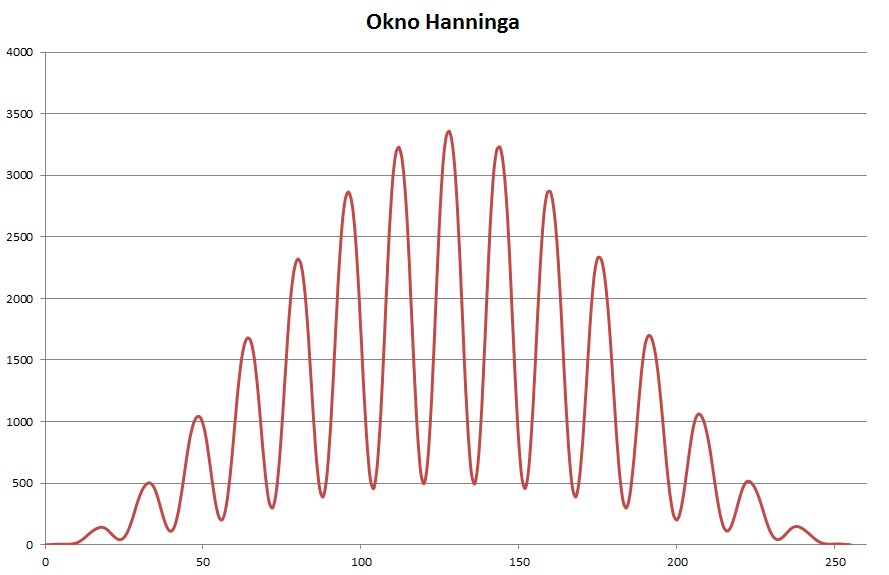
Rys. 7. Sygnał sinusoidalny przemnożony przez okno Hanninga
- Okno Flat Top o równaniu [10]:

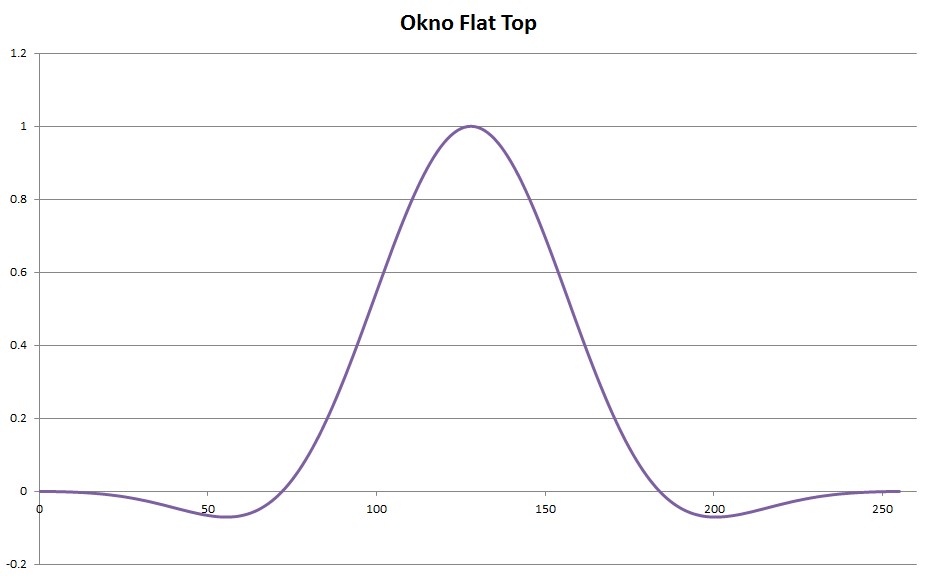
Rys. 8. Okno Flat top
Sygnał sinusoidalny przemnożony przez okno Flat top:
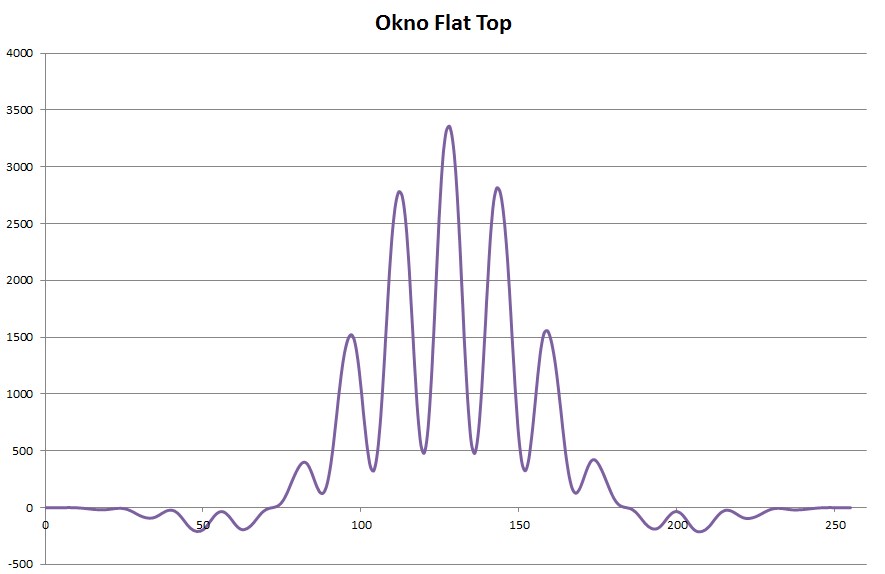
Rys. 9. Okno Flat Top
- Okno prostokątne, które zastosowałem u siebie w projekcie. Można zrealizować poprzez wyszukanie z bufora minimum lub maksimum, a następnie zebranie próbek do FFT (w moim przypadku 256 próbek). W projekcie wykorzystuję sygnał czysto sinusoidalny jako sygnał wzbudzający. Podczas implementacji okien do projektu doszedłem do wniosku, że najmniejszy wyciek widma jest dla okna prostokątnego. Zastosowałem okno prostokątne, które zaczyna się w wartości maksymalnej sinusoidy, a kończy po 256 próbkach.
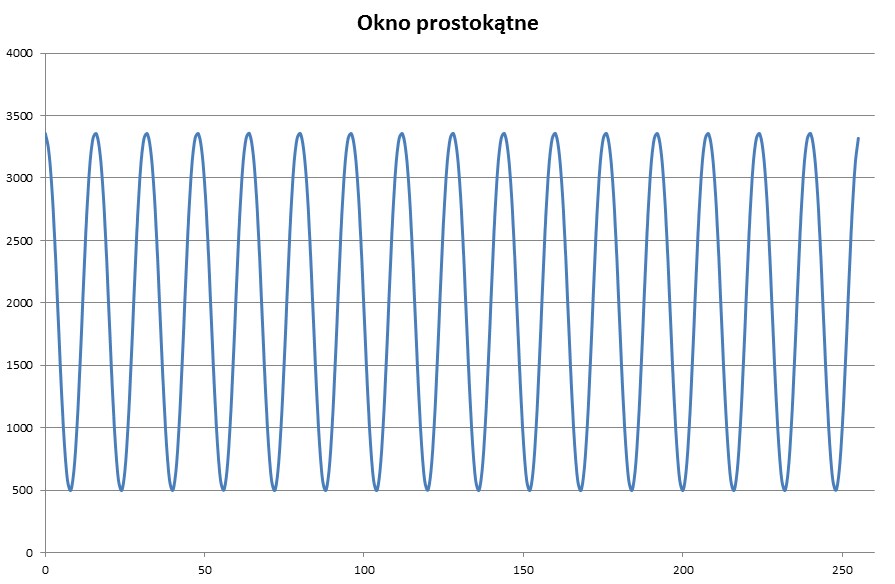
Rys. 10. Okno prostokątne
Wyznaczenia fazy:
Fazę sygnału można wyznaczyć z następującego wzoru:
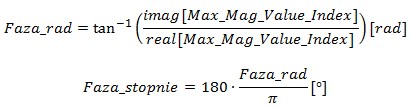
Wdrożenie biblioteki CMSIS do projektu:
Kroki wdrożenia biblioteki CMSIS do projektu:
- Pobieramy plik nagłówka: arm_math.h z oficjalnego repozytorium Github ARM Include.
- Następnie pobieramy plik obiektowy, w moim przypadku: libarm_cortexM4lf_math.a, także z oficjalnego repozytorium Github ARM GCC. Pobrałem plik lf, ponieważ wspiera sprzętowy FPU (Floating Point Unit).
- Wklejamy plik nagłówkowy w folder Core/Inc naszego projektu.
- Dodajemy biblioteki arm_math w sekcji Include oraz wybieramy procesor, w moim przypadku ARM_MATH_CM4, ponieważ używam STM32F4.
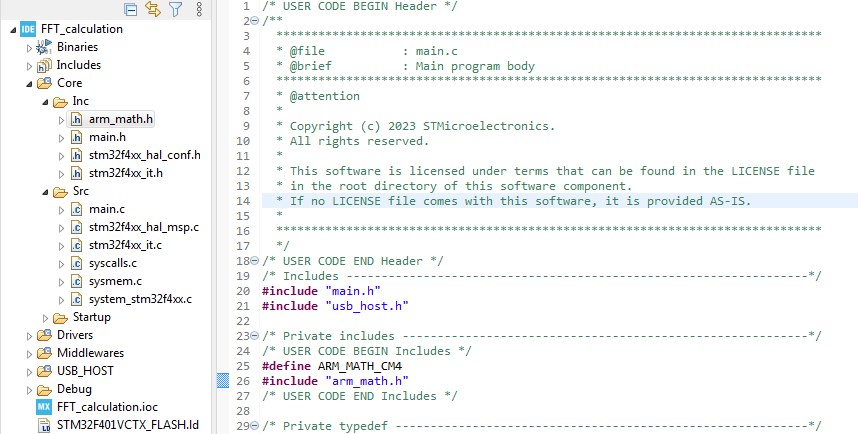
Rys. 11. Dodana biblioteka arm_math
5. Umieszczamy plik libarm_cortexM4lf_math.a w folderze, gdzie zapisany jest nasz projekt. Stworzyłem nowy folder w projekcie i tam przeniosłem plik libarm.
6. Ustawiamy linker, gdzie dodałem ścieżkę do biblioteki oraz samą bibliotekę libarm.
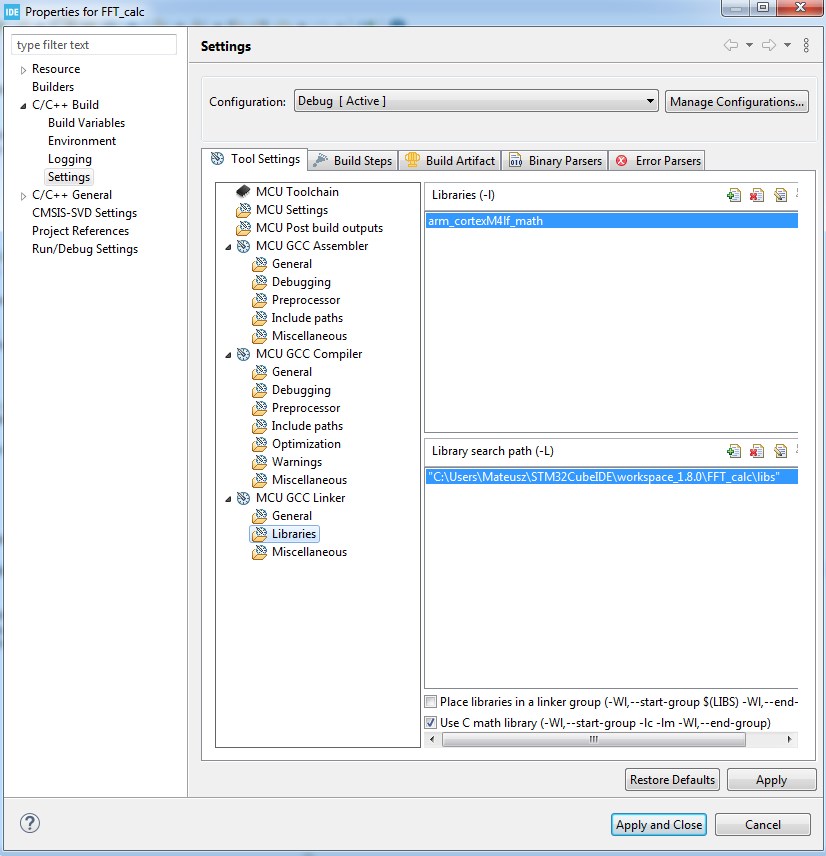
Rys. 12. Ustawienia linkera
Ustawienia przetwornika ADC:
Należy wykonać następujące kroki w celu poprawnej konfiguracji przetwornika ADC:
- Ustawienia timera, aby wyzwalał konwersję przetwornika z pożądaną częstotliwością, u mnie 80kHz, do czego użyłem następującego wzoru:
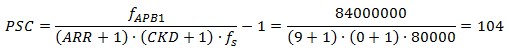
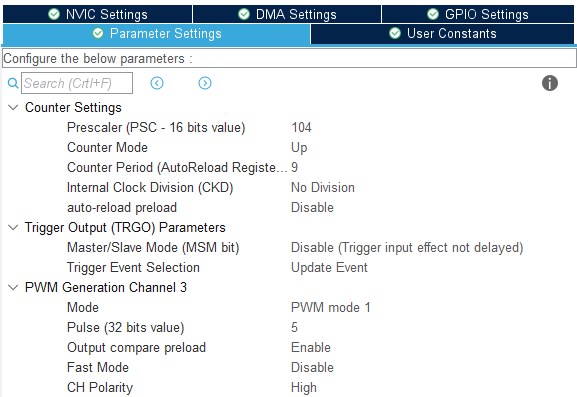
Rys. 13. Ustawienia timera w Cube
2. Ustawienia przetwornika ADC, źródłem wyzwalania konwersji jest timer 2:
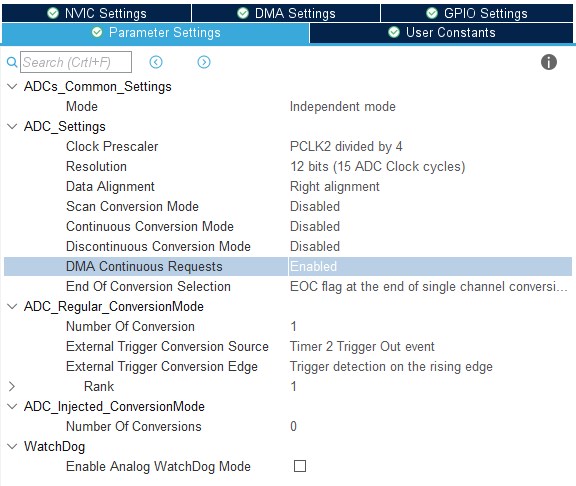
Rys. 14. Ustawienia przetwornika ADC w Cube
Podsumowanie:
We wpisie zawarłem informację wprowadzające do obliczenia FFT na procesorze STM32. W kolejnych wpisach przedstawię wykonanie obliczeń na procesorze oraz wyniki.
[1] Dostęp w internecie: https://www.nti-audio.com/en/support/know-how/fast-fourier-transform-fft[2] Dostęp w internecie: https://www.keil.com/pack/doc/CMSIS/DSP/html/index.html
[3] Dostęp w internecie: https://www.keil.com/pack/doc/CMSIS_Dev/DSP/html/group__RealFFT.html
[4] Dostęp w internecie: https://www.mdpi.com/2076-3417/12/2/591
[5] Dostęp w internecie: https://www.st.com/resource/en/application_note/an2834-how-to-get-the-best-adc-accuracy-in-stm32-microcontrollers-stmicroelectronics.pdf
[6] Dostęp w internecie: https://www.electronicdesign.com/technologies/analog/article/21798689/choose-the-right-fft-window-function-when-evaluating-precision-adcs
[7] Dostęp w internecie: https://www.edn.com/choosing-the-right-fft-window-function-while-testing-adcs/
[8] Dostęp w internecie: https://www.mathworks.com/help/signal/ref/blackmanharris.html
[9] Dostęp w internecie: https://www.mathworks.com/help/signal/ref/hann.html
[10] Dostęp w internecie: https://www.mathworks.com/help/signal/ref/flattopwin.html






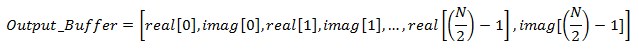
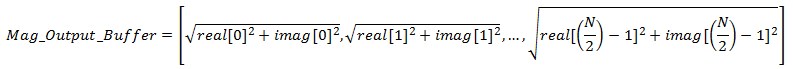
 Caroline Pannier – nowa dyrektorka targów electronica – analizuje sytuację gospodarczą branży i przedstawia wyniki
Caroline Pannier – nowa dyrektorka targów electronica – analizuje sytuację gospodarczą branży i przedstawia wyniki  Konstrukcja Ventiva Zoned Cooling™ – ukierunkowane chłodzenie powietrza dla urządzeń AI Edge
Konstrukcja Ventiva Zoned Cooling™ – ukierunkowane chłodzenie powietrza dla urządzeń AI Edge  Komunikacja dalekiego zasięgu oparta na technologii Qualcomm dla robotyki i dronów
Komunikacja dalekiego zasięgu oparta na technologii Qualcomm dla robotyki i dronów 






