W kolejnym wpisie, dotyczącym szybkiej transformaty Fouriera, Mateusz Pluta przedstawi program służący do obliczenia FFT oraz wyniki na podstawie sygnału z generatora funkcyjnego. Zaprezentuje też, w jaki sposób częstotliwość próbkowania oraz okna wpływają na wyciek widma.

Zachęcamy do przeczytania pierwszej cześci serii: Obliczenie FFT na mikrokontrolerze STM32 (1) – Biblioteka CMSIS, wyciek widma, okna wykorzystywane do FFT, wdrożenie w projekcie

Zakres wpisu:

• Program obliczający FFT
• Sygnał z timera informujący o częstotliwości próbkowania
• Wyniki FFT
• Wyciek widma spowodowany złym doborem częstotliwości próbkowania
• Wyciek widma spowodowany użyciem okien innych niż prostokątne, kiedy sygnał jest okresowy

Więcej artykułów na Blog IntHou

Program obliczający FFT

Funkcje uruchamiające używane peryferia: timer 2 wyzwalający konwersję oraz DMA przetwornika analogowo-cyfrowego:

HAL_ADC_Start_DMA(&hadc1, (uint32_t*)&ADC_Buffer, BUFFER_SIZE);
HAL_TIM_Base_Start(&htim2);
HAL_TIM_PWM_Start(&htim2, TIM_CHANNEL_3);

Inicjalizacja FFT:

arm_rfft_fast_instance_f32 fft_handler;
arm_rfft_fast_init_f32(&fft_handler, fftSize);

Funkcja obliczająca FFT: Bufor wejściowy do FFT składa się z 255 próbek, od wartości maksymalnej. Jest to przebieg wejściowy wycięty oknem prostokątnym.

Napięcie referencyjne na Discovery wynosi 3,0 V, więc wprowadzona składowa stała 1,4 V na generatorze będzie wynosiła w LSB 1911. Ta wartość jest odejmowana w linii 19. Bez usunięcia offsetu największy prążek będzie dla częstotliwości 0, czyli składowej stałej.

W poniższym kodzie używane jest okno prostokątne, dlatego zakomentowłem linie od 22 do 32. Jeśli chcesz użyć innego okna niż prostokątne, należy odkomentować wybrane okno, a zakomentować część dotyczącą okna prostokątnego.

void FFT_Calc()
  {
      if(Buffer_FFT_Status==1)
      {
          First_calculation_loop=0;
          /*Szukanie pierwszego maksimum przy którym naładowane będą kondensatory filtrujące*/
          for(uint16_t i=150; i<200; i++)
          {
              if(ADC_Buffer[i]>Max_value)
              {
                  Max_value_index=i;
                  Max_value=ADC_Buffer[i];
              }
          }

          /*Bufor zawierający 256 próbkek od wartości maksymalnej stworzony do prezentacji przebiegu wchodzącego do FFT*/
          for(uint16_t i=0; i<FFT_SAMPLES; i++)
          {
              Input_Buffer[i]= ((float32_t) (ADC_Buffer[Max_value_index+i]))-1911.0;
          }

          /*for(uint16_t i=0; i<FFT_SAMPLES; i++)
          {
                 //Blackman-Harris window
                 //Input_Buffer_Window[i]=(0.35875 - 0.48829 * cosf((2.0*PI*i) / (FFT_SAMPLES)) + 0.14128 * cosf((4.0*PI*i) / (FFT_SAMPLES)) - 0.01168 * cosf((6.0*PI*i) / (FFT_SAMPLES))) * Input_Buffer[i];

                //Hanning Window
                //Input_Buffer_Window[i]=(0.5 * (1-cosf((2.0*PI*i) / (FFT_SAMPLES)))) * Input_Buffer[i];

                //Flat top window
                //Input_Buffer_Window[i]=(0.21557895 - 0.41663158 * cosf((2*PI*i) / (FFT_SAMPLES)) + 0.277263158 * cosf((4*PI*i) / (FFT_SAMPLES)) - 0.083578947 * cosf((6*PI*i) / (FFT_SAMPLES)) + 0.006947368 * cosf((8*PI*i) / (FFT_SAMPLES))) * Input_Buffer[i];
           }*/
          
          /*Bufor używany do obliczenia FFT, został stworzony, ponieważ funkcja FFT modyfikuje bufor wejściowy*/
          for(uint16_t i=0; i<FFT_SAMPLES; i++)
          {
              
              Input_Buffer_FFT[i]=Input_Buffer[i];
            /*Input_Buffer_FFT[i]=Input_Buffer_Window[i];*/

          }

          /*Funkcja obliczająca FFT*/
          arm_rfft_fast_f32(&fft_handler,Input_Buffer_FFT,Output_Buffer_FFT, ifftFlag);

          /*Funkcja obliczająca moduł z wartości rzeczywistej i urojonej dla każdego z prążków*/
          arm_cmplx_mag_f32(Output_Buffer_FFT, Mag_Output_Buffer, fftSize/2);

          /*Funkcja szukająca wartości maksymalnej*/
          arm_max_f32(Mag_Output_Buffer, fftSize/2, &Max_Value_Mag_Buffer, &Max_Mag_Index);

          /*Wydzielenie wartości rzeczywistej i urojonej z tablicy wyników FFT*/
          for(uint16_t i=0; i<FFT_SAMPLES_HALF; i++)
          {
              real_Output_Buffer[i]=Output_Buffer_FFT[i*2];
              imag_Output_Buffer[i]=Output_Buffer_FFT[(i*2)+1];
          }

          /*Tablica przesunięcia fazowego dla każdeo prążka*/
          for(uint16_t i=0; i<FFT_SAMPLES_HALF; i++)
          {
               Angle_Output_Buffer[i]=atan2f(imag_Output_Buffer[i], real_Output_Buffer[i]);
          }

          /*Przesunięcie fazowe maksymalnego prążka*/
          Angle_Max_Output_Buffer=atan2f(imag_Output_Buffer[Max_Mag_Index],
real_Output_Buffer[Max_Mag_Index]);

          /*Informacja o zakończeniu obliczeń*/
          Calculation_finished=1;

          /*Zerowanie wartości maksymalnej*/
          Max_value=0;

      }
  }

Funkcja Callback informuje o zebraniu 512 próbek do bufora wejściowego. Zbieram dwa razy większą liczbę próbek niż potrzebuję do FFT, aby mieć pewność, że będę miał wystarczającą liczbę próbek.

void HAL_ADC_ConvCpltCallback(ADC_HandleTypeDef* hadc)
{
    if(hadc->Instance == ADC1)
    {
        if(Calculation_finished==1 || First_calculation_loop==1)
        {
            Calculation_finished=0;
            Buffer_FFT_Status=1;
        }
    }
}

Sygnał z timera 2 informujący o częstotliwości próbkowania

Częstotliwość próbkowania została ustawiona na 80 kHz. Można to zaprogramować poprzez wyzwalanie przetwornika ADC za pomocą sygnału z timera 2:

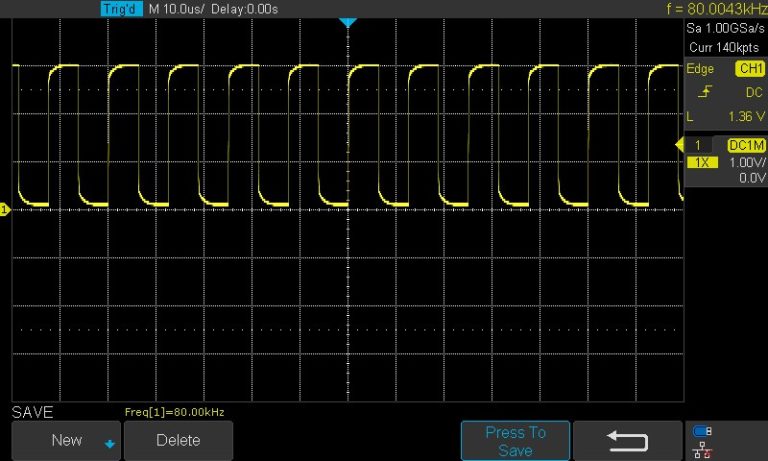
Rys. 1. Częstotliwość timera 2

Wyniki FFT

Przebieg sygnału z generatora funkcyjnego o częstotliwości 10 kHz, na którym będzie wykonywane FFT:

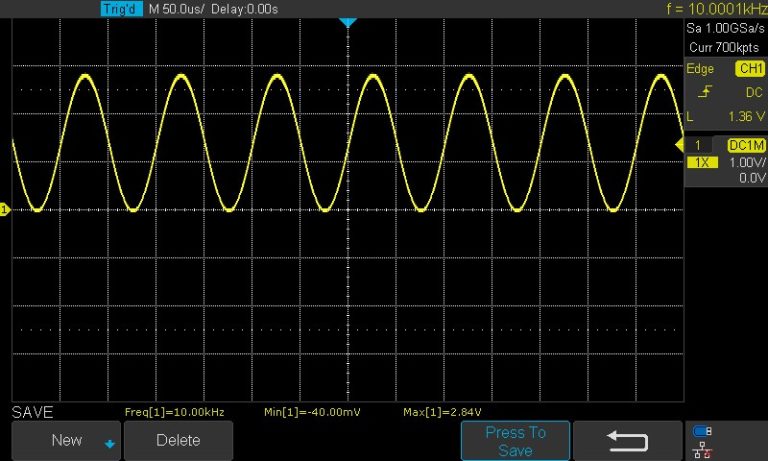
Rys. 2. Przebieg sinusoidalny z generatora funkcyjnego o częstotliwości 10 kHz

Bufor wejściowy FFT to fragment przebiegu wycięty oknem prostokątnym, składający się z 256 próbek, przesunięty o składową stałą w celu wyznaczenia największej energii z częstotliwości przebiegu. Próbki zostały odczytane za pomocą programu STMStudio.

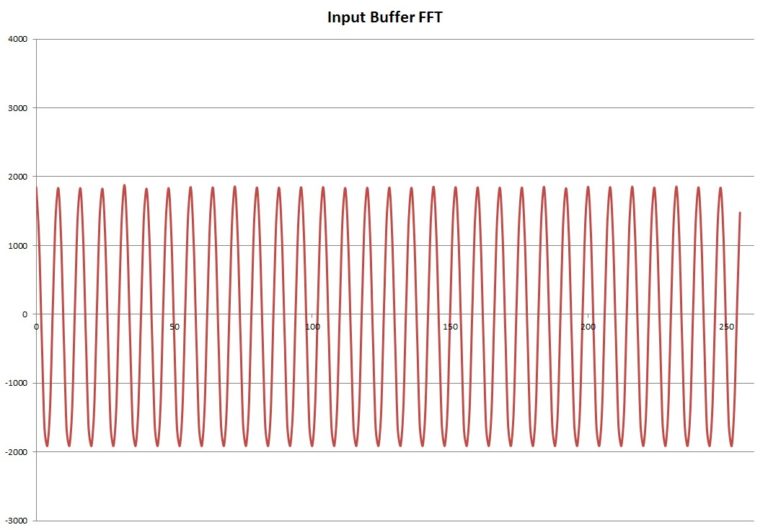
Rys. 3. Bufor 256 próbek przesunięty o składową stałą

Po wykonaniu FFT na przebiegu, odczytano 32 prążek jako prążek o największej energii:

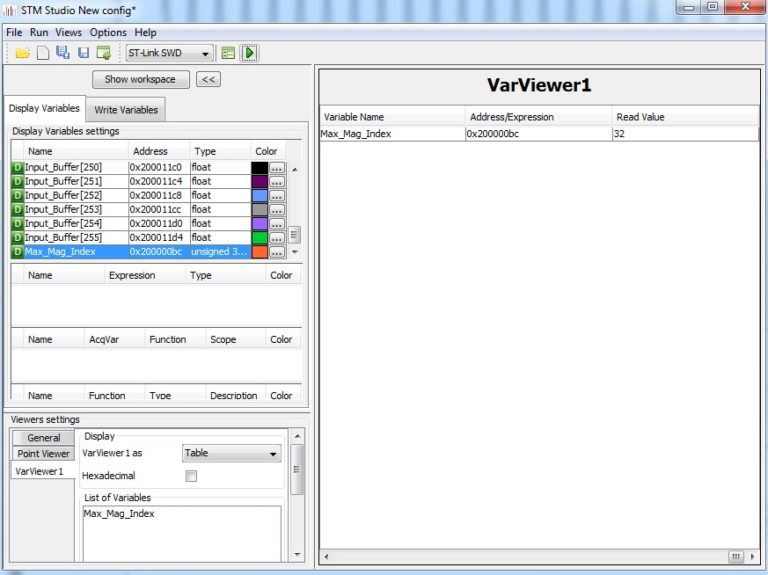
Rys. 4. Numer prążka o największej energii

Wykorzystując okno prostokątne oraz 2ⁿ okresów, nie doświadczamy zjawiska wycieku widma, co widać na rys. 4. Podczas jednego okresu sinusoidy o częstotliwości 10 kHz zbieranych jest 8 próbek, a więc w buforze składającym się z 256 próbek będzie 32 okresy.

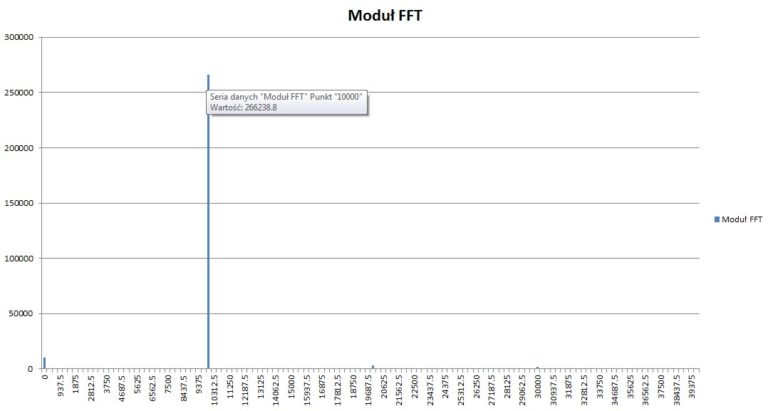
Rys. 5. Prążki przebiegu o częstotliwości 10 kHz z oknem prostokątnym

Wyciek widma spowodowany złym doborem częstotliwości próbkowania

Teraz przy takich samych ustawieniach częstotliwości próbkowania podałem sygnał sinusoidalny o częstotliwości 16 kHz, czyli 5 okresów. Warunek o 2ⁿ okresów nie został spełniony.

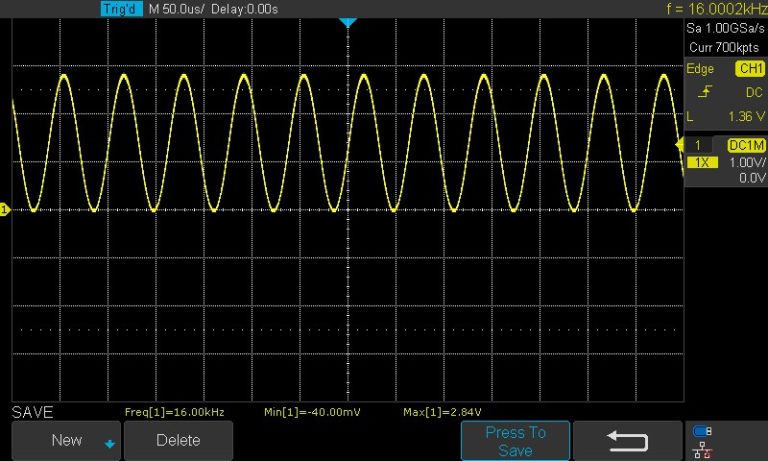
Rys. 6. Przebieg sygnału sinusoidalnego z generatora funkcyjnego o częstotliwości 16 kHz

Niespełniony warunek o liczbie 2ⁿ okresów skutkuje tym, że pojawia się wyciek widma, co można zaobserwować na rys. 7.

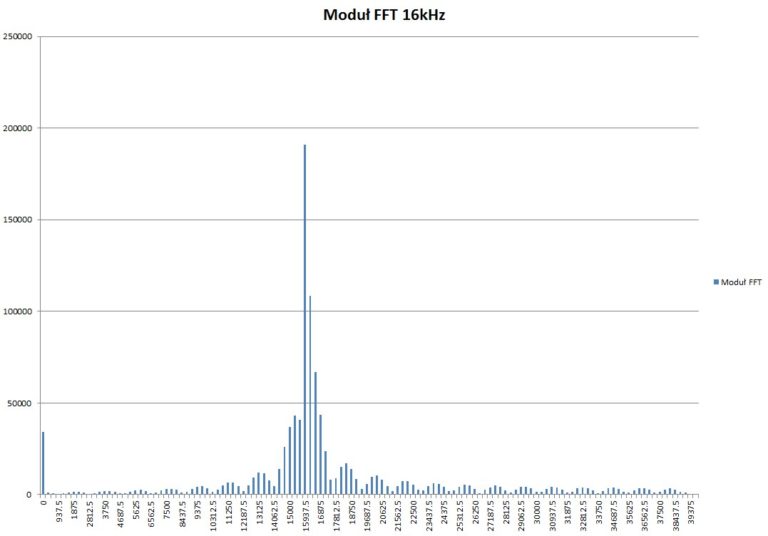
Rys. 7. Prążki przebiegu o częstotliwości 16 kHz i częstotliwości próbkowania 80kHz

Wyciek widma spowodowany użyciem okien innych niż prostokątne, kiedy sygnał jest okresowy

Okna są użyteczne, kiedy sygnał jest nieokresowy. Kiedy sygnał jest okresowy, najlepszym wyborem będzie okno prostokątne, co udowadniają poniższe wyniki dla różnych okien. Obliczenia FFT z wykorzystaniem okien zostały wykonane na podstawie przebiegu z rys. 2 (10 kHz), przy tej samej częstotliwości próbkowania 80 kHz.

Okno Blackmana-Harrisa:

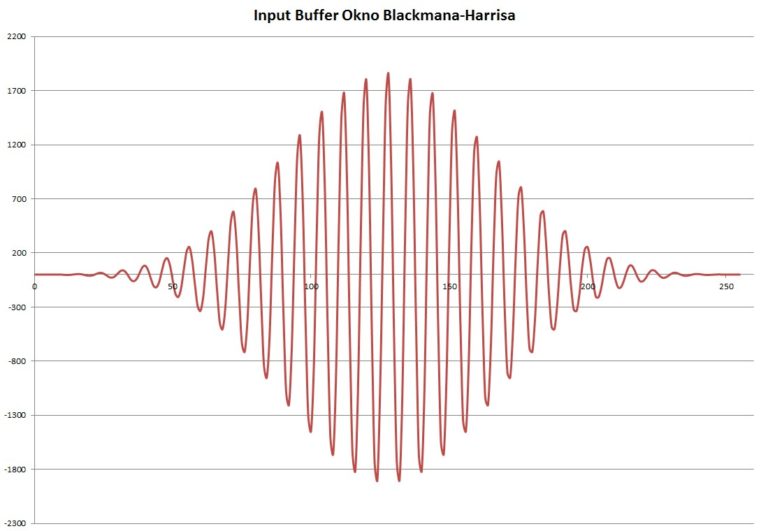
Rys. 8. Przebieg wejściowy przemnożony przez okno Blackmana-Harrisa

Obliczone spektrum z przebiegu przemnożonego przez okno Blackmana-Harrisa:

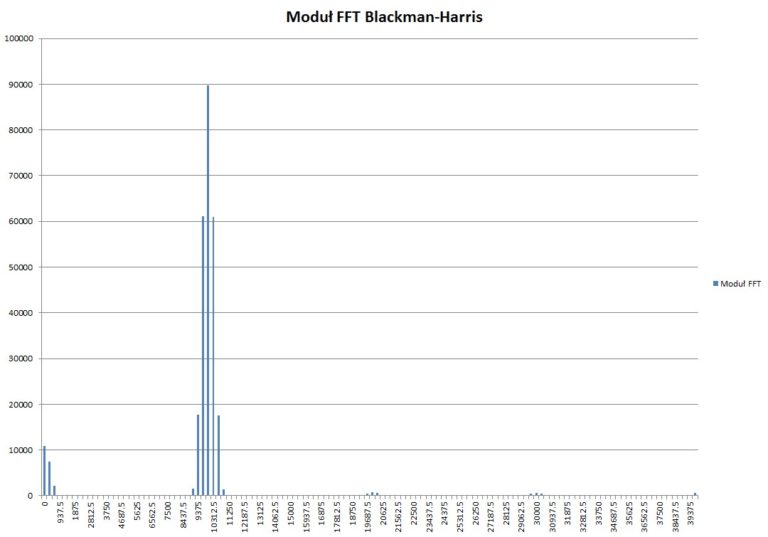
Rys. 9. Obliczone spektrum z przebiegu 10 kHz z oknem Blackmana-Harrisa

Okno Hanninga:

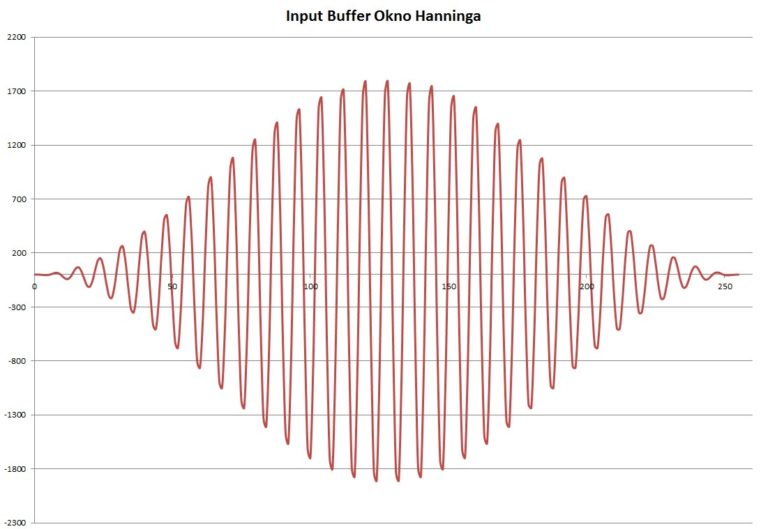
Rys. 10. Przebieg wejściowy przemnożony przez okno Hanninga

Obliczone spektrum z przebiegu przemnożonego przez okno Hanninga:

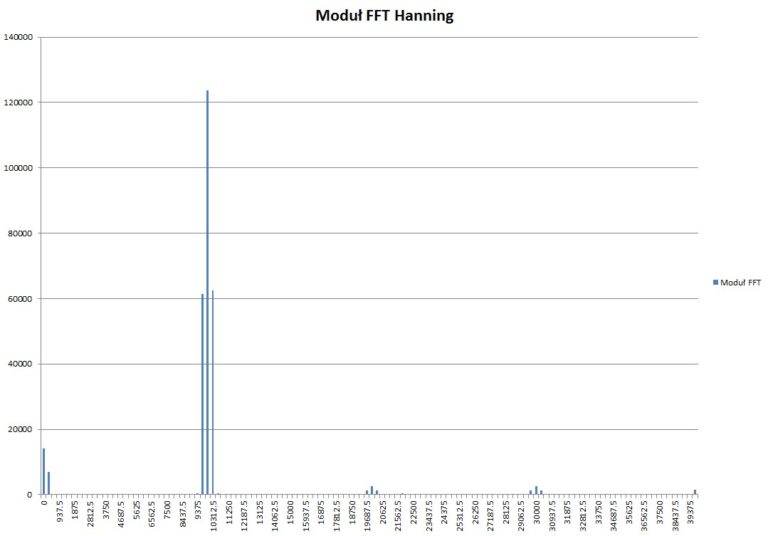
Rys. 11. Obliczone spektrum z przebiegu 10 kHz z oknem Hanninga

Okno flat top:

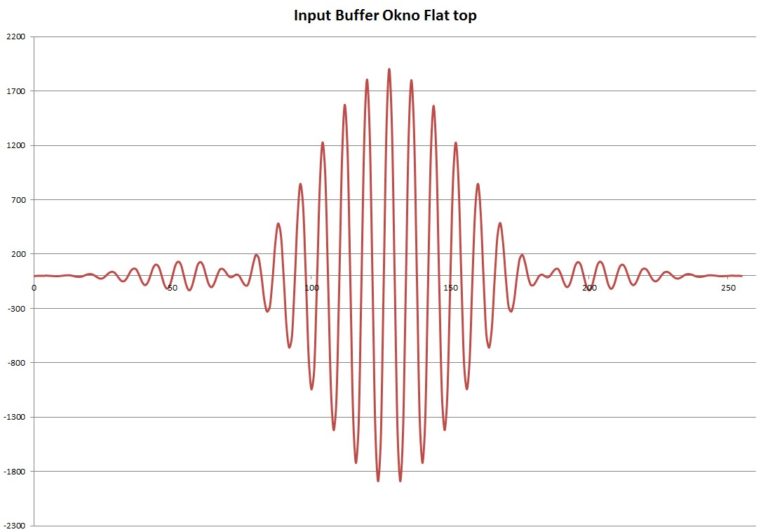
Rys. 12. Przebieg wejściowy przemnożony przez okno Flat top

Obliczone spektrum z przebiegu przemnożonego przez okno Flat top:

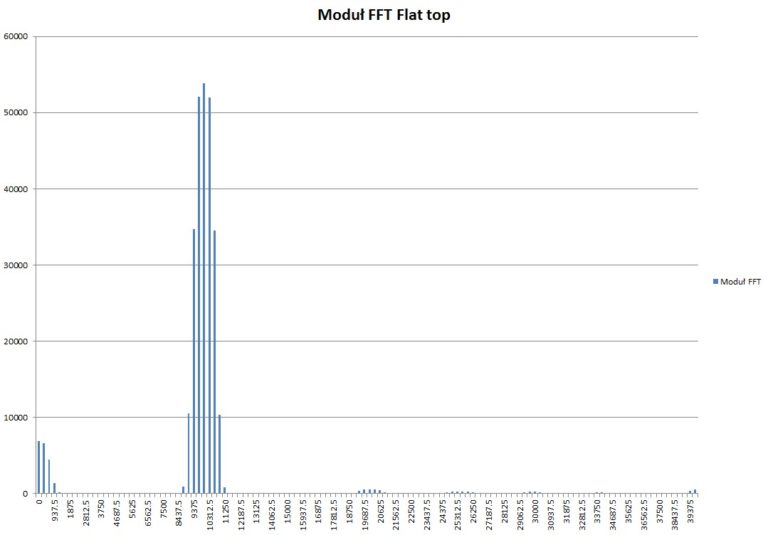
Rys. 13. Obliczone spektrum z przebiegu 10 kHz z oknem Flat top

Podsumowanie

We wpisie zawarłem informację na temat programu służącego do wykonania FFT, przedstawiłem wyniki oraz omówiłem czynniki, które mają wpływ na wyciek widma.