ESR to parametr kondensatorów, którego znaczenie jest często ignorowane przez konstruktorów urządzeń elektronicznych. Wynika to z faktu, że zwykle nie ma on istotnego wpływu na działanie układu. Niestety, zdarzają się nieliczne przypadki, w których jego znaczenie jest wręcz krytyczne. Przekonałem się o tym osobiście podczas pracy nad urządzeniem, w którym został zastosowany przetwornik analogowo-cyfrowy AD7606 firmy Analog Devices. Producent tego układu – firma, która niewątpliwie należy do liderów rynku (nie lubię takich określeń, ale nie można się z nim nie zgodzić) dawał mi pewną cichą gwarancję, że zastosowanie przetwornika AD7606 pozwoli uzyskać doskonałe parametry urządzenia. Już przy pierwszej próbie uruchomienia okazało się jednak, że wyniki pomiarów są wręcz tragiczne.  Przetworzony cyfrowo sygnał analogowy wizualizowany w programie był obarczony nieakceptowanie wielkimi szumami. Początkowo winą obarczyłem wszystko co mogło wydarzyć się w części analogowej, a były to tensometry z odpowiednimi wzmacniaczami oddalone o kilkadziesiąt centymetrów od płytki z przetwornikiem ADC i obsługującym go mikrokontrolerem. Teoretycznie więc konfiguracja taka mogła być podatna wszystkie możliwe zakłócenia i szumy z otoczenia. Przewidując taką możliwość wzmacniacze tensometryczne zostały umieszczone blisko samych tensometrów, co pozwoliło uniknąć przesyłania sygnałów o bardzo małych poziomach długimi przewodami. Przedstawiany tu przypadek był o tyle tajemniczy, że nie był to pierwszy taki zestaw, który uruchamiałem. We wcześniejszych problem z szumami nie występował.

Pomiary oscyloskopowe sygnałów na wejściu DAC nie wykazywały tak wielkich szumów, jakie ujawniały się po przetworzeniu w programie. Rozpoczęło się więc dochodzenie, co może być przyczyną takiej sytuacji. W wyniku podjętych działań moją uwagę zwróciła mała adnotacja zamieszczona w nocie katalogowej przetwornika (rys. 1).

Rys. 1. Fragment noty katalogowej przetwornika AD7606 z ważną uwagą dotyczącą wejść REFCAPA i RECAPB

Wynika z niej, że wyprowadzenia REFCAPA i REFCAPB przetwornika powinny być zablokowane do masy kondensatorem ceramicznym Low ESR. Tymczasem pierwotnie beztrosko wlutowałem pierwszy, wzięty z szuflady zwykły kondensator elektrolityczny 10 μF. Szybkie poszukiwania wykazały, że nie mam pod ręką kondensatorów ceramicznych 10 μF, tylko elektrolity, ale za to z grupy Low ESR. Po błyskawicznej wymianie okazało się, że problemy z szumami na szczęście zniknęły. A już miałem montować nowe moduły wzmacniaczy tensometrycznych, które pierwotnie obarczałem kłopotami. W pierwszych egzemplarzach prawdopodobnie sięgałem do torebki, w której były kondensatory Low ESR. No cóż, gdybym stosował zasadę tracebility, prawdopodobnie do takiego zdarzenia by nie doszło.

Przypadek na tyle mnie zaintrygował, że postanowiłem zająć się bliżej metodą pomiarów ESR w warunkach, nazwijmy to domowych.

ESR – zaglądamy do środka kondensatora

ESR, to Equivalent Series Resistance, czyli zastępcza rezystancja szeregowa. Taki parametr w przypadku kondensatora może nieco dziwić, bo skąd niby miałaby się brać rezystancja w kondensatorze? Jeśli dokładniej przyjrzymy się budowie tego elementu, można jednak wyobrazić sobie, że może to być np. rezystancja wyprowadzeń, ale przecież jest ona liczona w ułamkach oma, więc czy ma aż tak istotne znaczenie? Jak się okazuje w niektórych aplikacjach ma, i to na tyle duże, że eliminuje dany element z użycia. Nie może więc dziwić, że jedną z pierwszych czynności serwisantów np. zasilaczy, przetwornic czy wzmacniaczy akustycznych jest wymiana wszystkich kondensatorów elektrolitycznych, nawet bez głębszej analizy ich stanu i kondycji. Nieprzyjemną cechą kondensatorów jest to, że ulegają starzeniu. Widoczną cechą problemów może być wylewający się z aluminiowej obudowy kondensatora elektrolit, który w miarę upływu czasu pod wpływem różnych zjawisk, m.in. temperatury zwiększa swoją objętość. Jest to możliwe, gdyż kubki kondensatorów elektrolitycznych mają specjalne nacięcia rozszczelniające w razie potrzeby obudowę. Bywają też stosowane zawory bezpieczeństwa zapobiegające spektakularnym eksplozjom. Jeśli proces przebiega zbyt szybko może dochodzić do groźnych zdarzeń. Temperatura wewnątrz kondensatora ulega zwiększeniu z powodu wysokiej temperatury otoczenia, a także wskutek… samopodgrzewania się. I znowu można się zdziwić. Przecież kondensator jest elementem biernym, więc moc czynna zamieniająca się w ciepło nie powinna się w nim wydzielać. Ale jest tak w kondensatorze idealnym, a ten rzeczywisty ma niezerowy ESR. Moc czynna równa I²R ma więc prawo wydzielić się w samym jego środku.

Jak widać, rzeczywisty kondensator zawiera w sobie nie tylko czystą pojemność, ale też szereg parametrów ekwiwalentnych, za pomocą których można stworzyć mniej lub bardziej wierny model kondensatora. W tym najbardziej szczegółowym sama pojemność musiałaby być również rozłożona na czynniki przeplatane z rozłożonymi rezystancjami a nawet indukcyjnościami. Takie schematy różniłyby się w zależności od typu kondensatora. Inny byłby dla kondensatora elektrolitycznego, inny dla ceramicznego, jeszcze inny dla polimerowego itd. Aż tak dokładne modelowanie nie ma jednak większego uzasadnienia dla konstruktora projektującego większość układów elektronicznych. Ograniczymy się zatem do trzech elementów przestawionych na rys. 2. W schemacie zastępczym występuje więc czysta pojemność C, rezystancja równoległa Rp odzwierciedlająca straty w dielektryku i rezystancja szeregowa Rs, którą będziemy utożsamiać z interesującym nas parametrem ESR. Można by ewentualnie dodać jeszcze indukcyjność Ls, która byłaby połączona szeregowo z Rs, ale w naszej analizie parametr ten zostanie pominięty. Należy jednak pamiętać, że w notach katalogowych indukcyjność ta jest często podawana jako ESL (Equivalent Series Inductance).

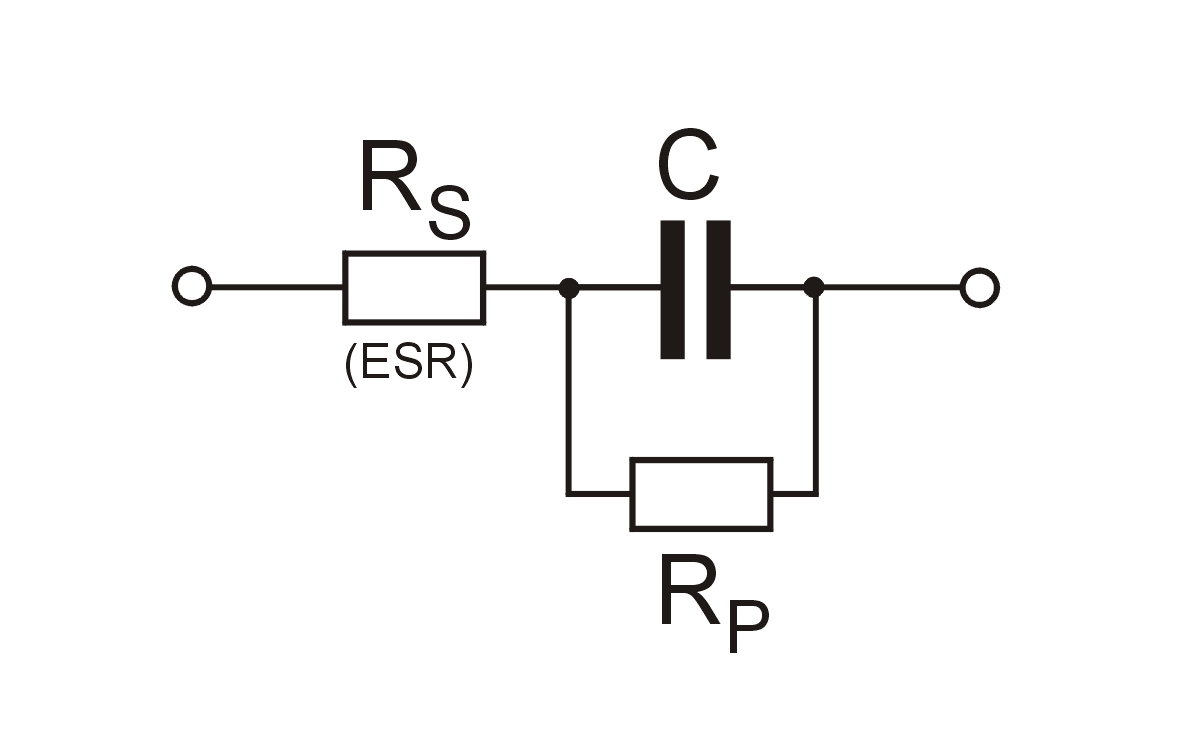
Rys. 2. Schemat zastępczy kondensatora

Jak mierzyć ESR?

Z pomiarem ESR kondensatora jest pewien problem. Po pierwsze jest to parametr o zwykle bardzo małej wartości rzędu ułamków oma, po drugie, jest to parametr, którego nie można zmierzyć prostą metodą bezpośrednią. Tak naprawdę można, ale będzie o tym mowa w drugiej części artykułu. Na tym etapie rozważań konieczne jest opracowanie jakiejś metody, która udostępniałaby element Rs schematu zastępczego. Na szczęście, w praktyce nie jest konieczny bardzo dokładny pomiar ESR, wystarczające jest określenie przybliżonej jego wartości. Parametru tego nie oblicza się w trakcie projektowania układu, przyjmuje się, że ma wartość zerową. W wyniku starzenia się kondensatora ESR może natomiast wzrosnąć na tyle, że zaczyna ujawniać się jego niekorzystny wpływ. Należy ponadto pamiętać, że ESR zależy m.in. od pojemności kondensatora, jego napięcia znamionowego, wieku (wiemy już, że ESR rośnie wraz z upływem czasu) i innych czynników. Jak widać, w ogólnym przypadku trudno jest podać uniwersalne wskazówki pozwalające jednoznacznie ocenić jakość kondensatora określoną na podstawie pomiaru ESR. Pomocne są tabele, które łatwo można znaleźć w Internecie (tab. 1). Zawierają one wartości maksymalne ESR dla kondensatorów o różnych pojemnościach i różnych napięciach znamionowych. Ich przekroczenie może świadczyć o „zużyciu się” kondensatora i konieczności jego wymiany.

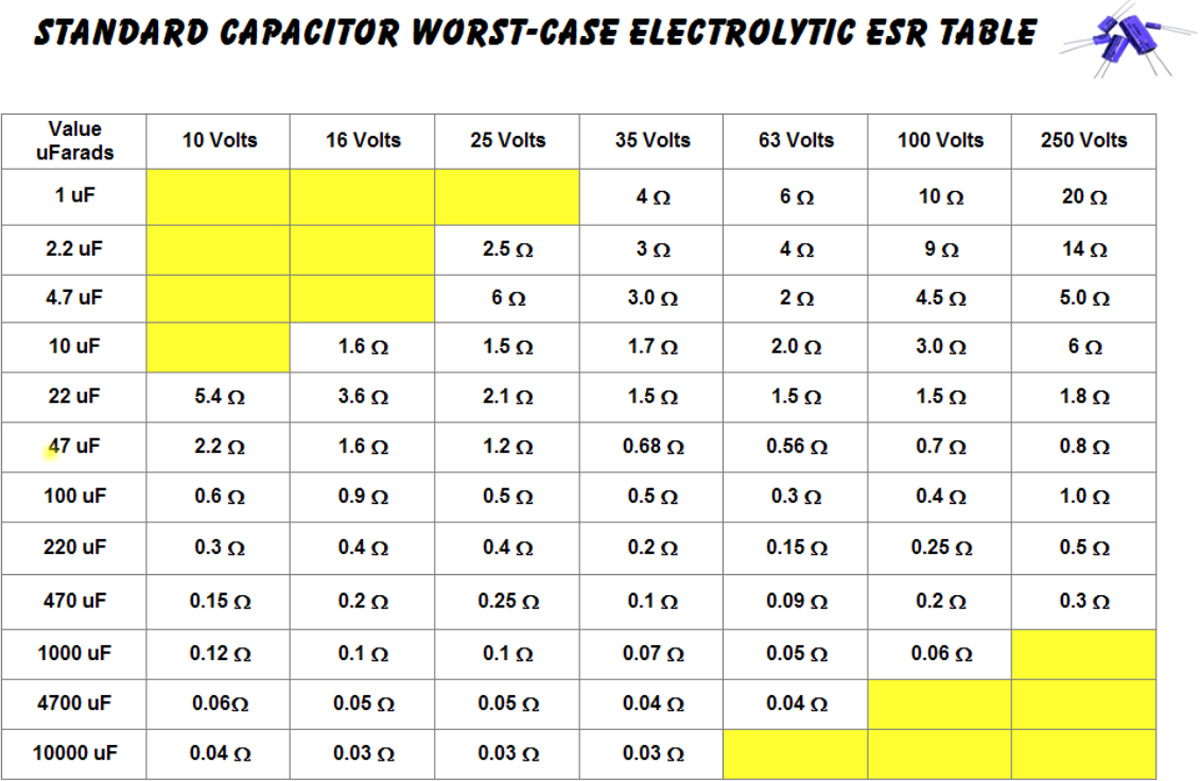
Tab. 1. Wartości krytycznych wartości ESR dla poszczególnych grup kondensatorów elektrolitycznych. Źródło:http://www.solidpost.com/doku.php?id=electronic:standard_capacitor_worst-case_electrolytic_esr_table

Chociaż w ogólnodostępnej literaturze można znaleźć wiele metod i specjalnych mierników, od bardzo tanich do średnio drogich, opracujemy własną metodę, do której potrzebny będzie generator przebiegu sinusoidalnego i dwukanałowy oscyloskop. Opracowanie metody będzie wymagało cofnięcia się do lekcji trygonometrii w szkole średniej i podstaw teorii obwodów. Zaczynamy.

Metoda #1 (techniczna) pomiaru ESR

Do opracowania metody posłużymy się modelem dość znacznie „zepsutego” kondensatora. Zabieg pogorszenia jego parametrów oddali nas wprawdzie nieco od świata realnego, ale znacznie ułatwi zrozumienie zależności między poszczególnymi elementami obwodu pomiarowego. Opracowanie metody wymaga wykonania kilku obliczeń na liczbach zespolonych i narysowania na ich podstawie wykresu wskazowego.

Układ pomiarowy (rys. 3) jest bardzo prosty. Składa się ze źródła sygnału sinusoidalnego V1, rezystora pomiarowego R₁ i elementów tworzących schemat zastępczy kondensatora. Są to: pojemności C i rezystancja szeregowa R_S reprezentująca szukany parametr ESR. Na schemacie zostały umieszczone punkty pomiarowe A, B i D, przy czym w układzie rzeczywistym mamy dostęp tylko do punktów A i B, natomiast punkt D leży wewnątrz kondensatora. Jest on jednak potrzebny do obliczeń ESR. Cały problem ogranicza się właściwie do znalezienia metody uzyskania dostępu do tego punktu. Będzie do tego pomocne wykreślenie wykresu wskazowego.

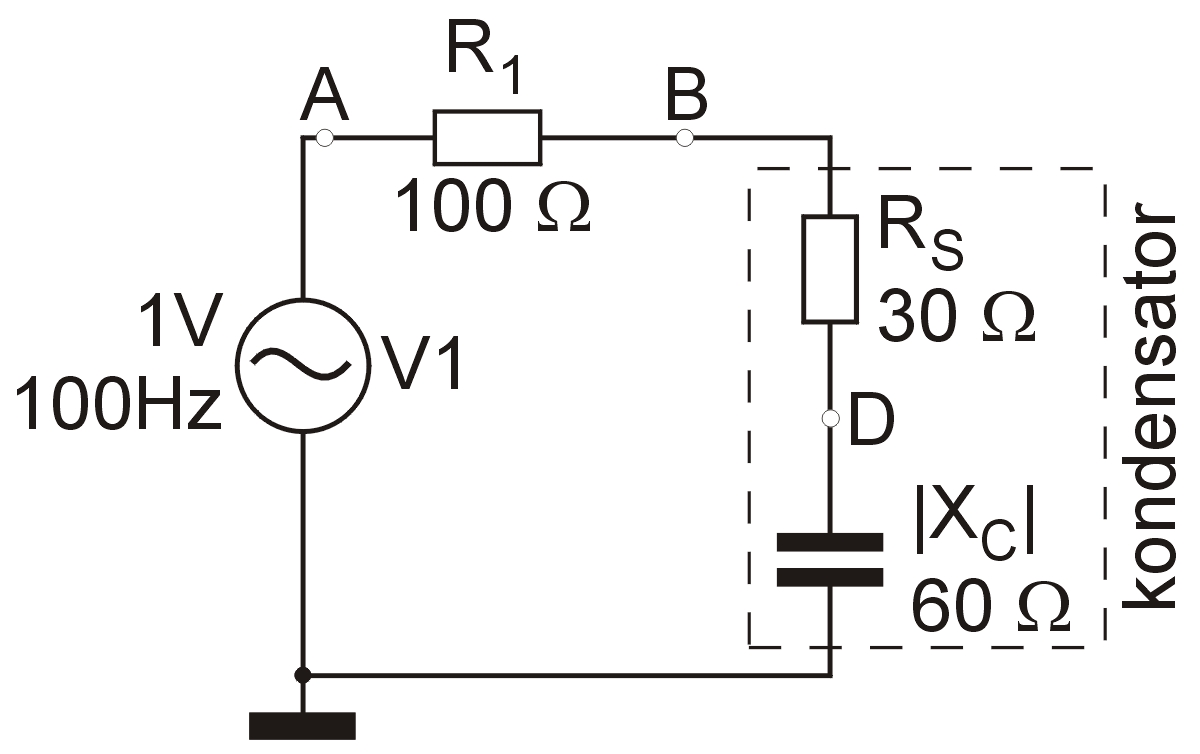
Rys 3. Układ używany do pomiaru ESR

Wykreślanie wykresu wskazowego

Do wykreślenia wykresu wskazowego potrzebne będzie obliczenie spadków napięć na wszystkich elementach obwodu. Do celów edukacyjnych zakładamy, że rezystancja źródła sygnału sinusoidalnego jest równa zero, rezystor pomiarowy R₁ ma rezystancję równą 100 Ω, rezystor R_S = 30 Ω (przyp. jest to ESR, którego szukamy, a tu przyjmujemy, że znamy jego wartość), reaktancja kondensatora X_C jest równa 60 Ω. Oznacza to, że dla ustalonej częstotliwości pomiaru , np. 100 Hz, pojemność jest równa ok. 26 μF. Komentarza wymaga przyjęcie tak dużej rezystancji R_S. W układzie rzeczywistym świadczyłaby o bardzo złej jakości kondensatora, ale będzie wygodniejsza w analizie. Zakładamy ponadto, że źródło generuje sygnał sinusoidalny o napięciu skutecznym 1 V i w stosunku do niego będziemy odnosić wszystkie przesunięcia fazowe. Można zatem zapisać, że V₁=U_A=1e^j0 V. Mając te dane możemy już obliczyć impedancję obwodu:

Prąd płynący w obwodzie jest równy:

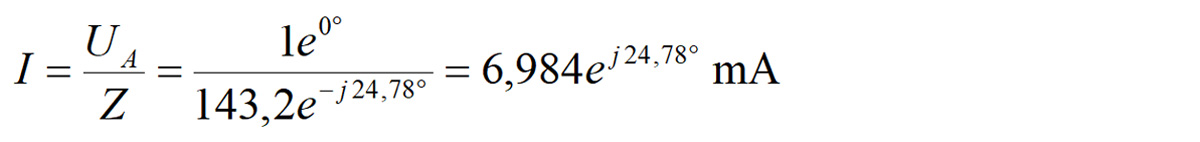
Napięcie na rezystorze pomiarowym R₁ wynosi:

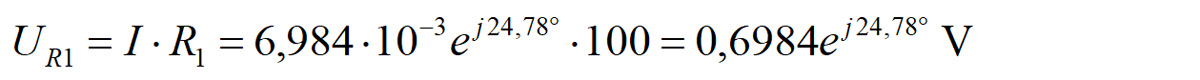
Teraz zajmiemy się obliczeniem impedancji samego kondensatora. Jest ona równa:

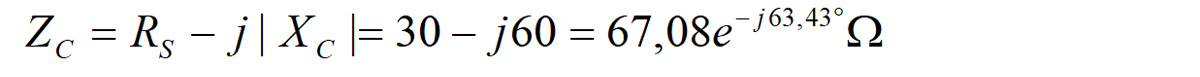
Znając tę impedancję można obliczyć napięcie w punkcie B. Jest ono równe:

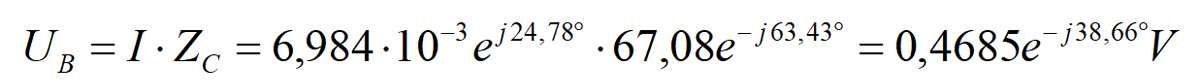
Napięcie na rezystorze szeregowym R_S (ESR) jest równe:

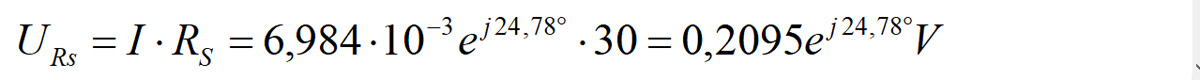
Pozostało jeszcze obliczenie napięcia na reaktancji kondensatora X_C. Jest ono równe:

Mamy już wszystkie dane potrzebne do narysowania wykresu wskazowego. Przesunięcie fazowe między prądem a napięciem źródła jest równe fazie prądu, a więc φ=24,78º. Dodatnia wartość oznacza, że w tym obwodzie prąd wyprzedza napięcie. Przyjmiemy, że wskazy symbolizujące poszczególne napięcia będą miały długość w centymetrach równą wartości danego napięcia pomnożonego przez 10. I jeszcze jedno ważne ustalenie: kąty mierzymy od osi OX (poziomej) w kierunku przeciwnym do ruchu wskazówek zegara. Kąt ujemny jest mierzony w kierunku przeciwnym.

Przyjęliśmy, że napięcie źródła jest równe 1e^j0º V, więc wskaz tego napięcia będzie miał długość 10 centymetrów i będzie położony poziomo ze zwrotem w prawo (rys. 4).

Rys. 4. Wskaz napięcia źródła V1

Źródło jest połączone między masą (oznaczenie na wykresie „O”) a punktem A, więc dla czytelności przy grocie tego wskazu umieszczamy literkę „A”, a przy jego początku będącego punktem odniesienia literkę „O”. Napięcie na rezystorze R₁ ma tę samą fazę co prąd, ponieważ rezystor fazy nie zmienia. Posługując się kątomierzem szkicujemy prostą przechodzącą przez punkt odniesienia „O” i nachyloną pod kątem φ=24,78º (możliwie jak najdokładniej – rys. 5). Teraz możemy już umieścić wskaz napięcia na rezystorze R₁. Mnożymy więc napięcie U_R1 przez 10 i wskaz o długości 6,98 cm zaczepiamy w punkcie „O” tak, aby był nachylony pod kątem φ=24,78º. Ponieważ kąt ten jest dodatni, grot tego wskazu będzie skierowany ku górze. Przy grocie umieszczamy literkę „B”.

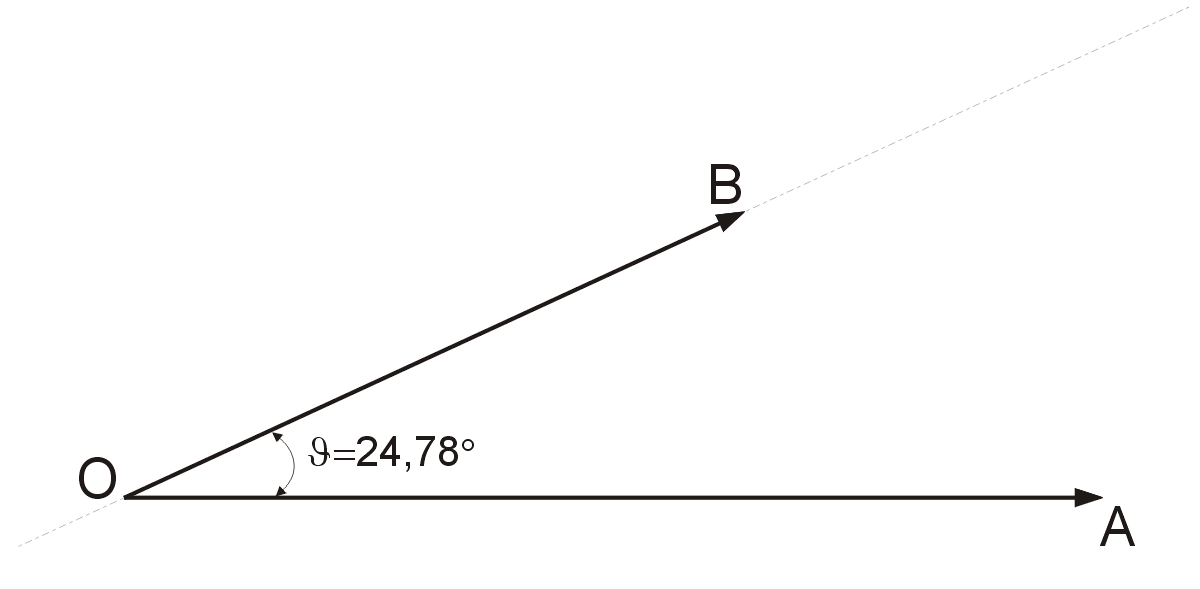
Rys. 5. Wykres wskazowy z naniesionym napięciem UR1

W naszych rozważaniach znamy rezystancję Rs, możemy więc narysować wskaz napięcia odkładającego się na tym rezystorze. Tak naprawdę, w trakcie pomiaru ESR będziemy szukać możliwości obliczenia tego napięcia, a dokładniej rezystancji R_S. Przez tę rezystancję płynie ten sam prąd, co przez R₁, więc wskaz będzie leżał na tej samej prostej co wskaz napięcia na R₁. Ponieważ rysowanie wykresu wskazowego odpowiada geometrycznemu sumowaniu napięć, więc wskaz napięcia U_Rs zaczepimy za koniec wskazu U_R1.  Będzie on miał długość 2,095 cm, gdyż obliczone napięcie U_Rs jest równe 0,2095 V. Koniec tego wskazu wyznacza położenie wirtualnego punkt D.

I teraz chwila prawdy. Napięcie na pojemności C (na jego reaktancji X_C) jest równe 0,4191e^-j65,22º, co oznacza, że odpowiadający mu wskaz powinien mieć długość 4,191 cn i musi być nachylony pod kątem 65,22º do osi OX. Łączymy więc punkty D i A na wykresie umieszczając przy punkcie A grot wskazu i sprawdzamy czy odległość między punktami D i A jest równa 4,191 cm?

Możemy jeszcze sprawdzić, czy wskaz BA ma długość odpowiadającą napięciu zmierzonemu w punkcie B. Powinien więc być równy 4,685 cm i musi tworzyć z osią OX kąt 38,66º.

Jeśli tak nie jest, oznacza to, że gdzieś został popełniony błąd – albo w obliczeniach, albo w rysowaniu wykresu. Po stwierdzeniu poprawności konstrukcji wykresu wskazowego można przystąpić do poszukiwania ESR.

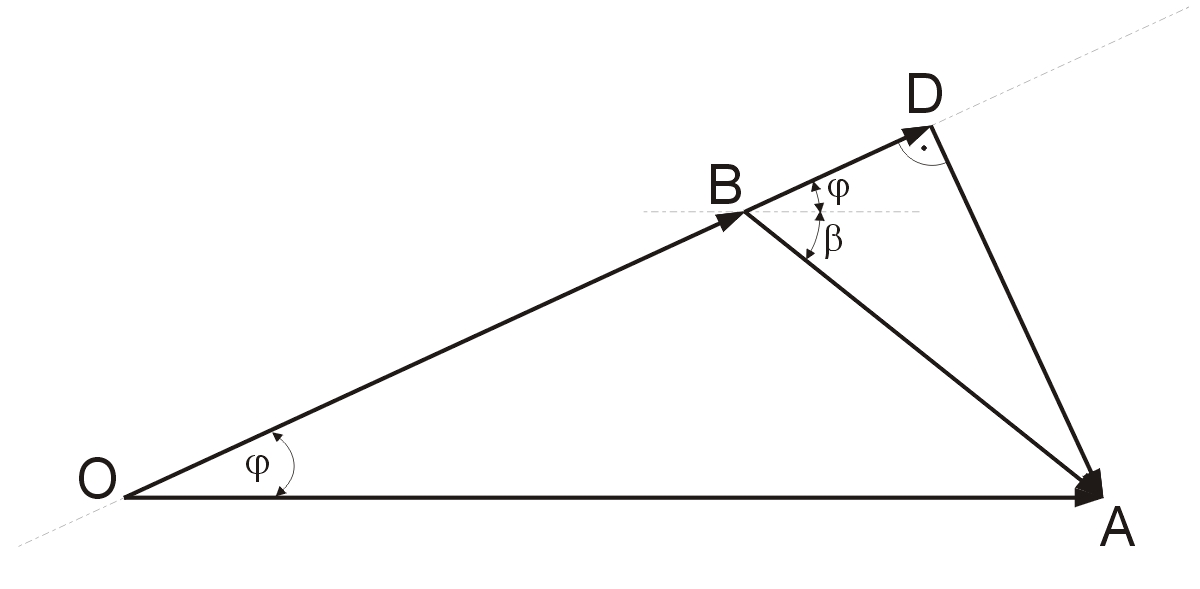
Rys. 6. Pełny wykres wskazowy układu pomiarowego

Zadanie z trygonometrii

Na rys. 7 jeszcze raz został przedstawiony wykres wskazowy z zaznaczonymi na niebiesko parametrami, które przy użyciu oscyloskopu będą możliwe do zmierzenia w układzie rzeczywistym. Naszym zadaniem jest obliczenie długości wskazu DB odpowiadającego spadkowi napięcia na rezystancji szeregowej kondensatora. Wszystkie elementy tego obwodu połączone są szeregowo, a więc przepływa przez nie ten sam prąd. Znając napięcie i prąd płynący przez R_S można obliczyć rezystancję szeregową R_S, czyli poszukiwany ESR.

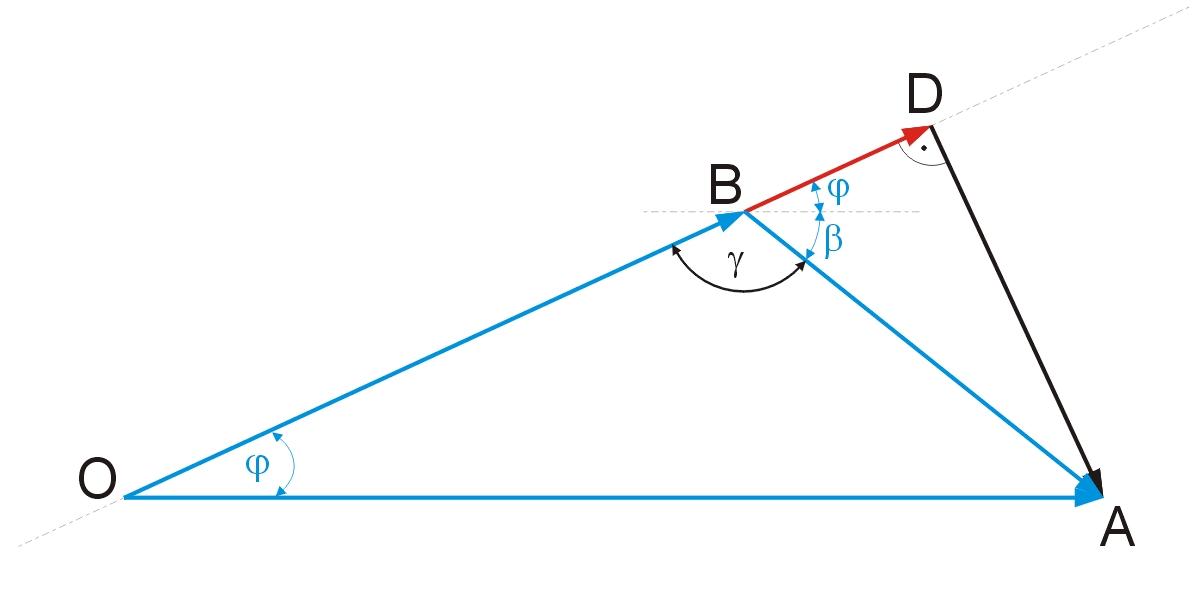
Rys. 7. Wykres wskazowy z zaznaczonymi na niebiesko parametrami mierzonymi i na czerwono poszukiwanym napięciem na rezystancji szeregowej wykorzystanym do obliczenia ESR

Wprawdzie oscyloskopem nie można bezpośrednio mierzyć natężenia prądu, ale większość współczesnych przyrządów ma zaimplementowane funkcje matematyczne. Po dołączeniu dwóch kanałów pomiarowych do punktów A i B (rys. 3) można łatwo obliczyć spadek napięcia na rezystorze R₁ (U_R1=U_AB=U_A-U_B). Teraz znając dokładną rezystancję R₁ (powinien to być dobrze określony rezystor o tolerancji 1% lub lepszej) można obliczyć prąd I płynący w obwodzie. I=U_R1/R₁. Również pomiar różnicy fazowej między dwoma przebiegami nie jest specjalnie trudny przy użyciu oscyloskopu. Duża część przyrządów ma nawet gotową funkcję przeznaczoną do tego celu, podającą gotowy wynik.

Obliczenie długości wskazu U_DB nie będzie zadaniem trudnym. Okazuje się, że trygonometria nie jest tak straszna, jak się powszechni sądzi. Rozpatrujemy trójkąt prostokątny ABD. Na szczęście znamy kąt φ=24,78º (przesunięcie fazowe między prądem a napiciem źródła U_A) i kąt β=38.66º (przesunięcie fazowe między napięciem U_B a napięciem źródła U_A). Teraz już wszystko jest jasne – z trójkąta prostokątnego ABD obliczamy:

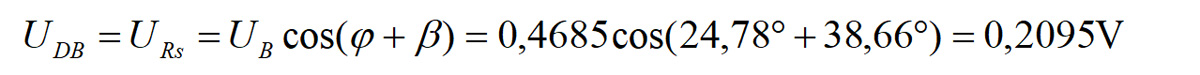
Jak widać, obliczone napięcie U_Rs jest zgodne z założeniami przyjętymi na początku.

Pozostało już tylko obliczenie ESR równego R_S:

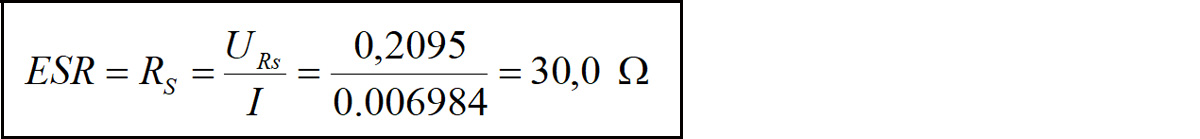
I w tym przypadku uzyskaliśmy zgodny wynik. Możemy spać spokojnie. Wyznaczenie ESR będzie w praktyce wymagało zmierzenia oscyloskopem napięcia U_A i U_B oraz kątów φ i β. Dla przypomnienia: są to przesunięcia fazowe między przebiegiem prądu a napięciem U_A i napięcia U_B również względem U_A. Przebieg prądu powinien być rysowany na podstawie równania I=(U_A-U_B)/R₁.

Ogólna zasada pomiaru ESR metodą techniczną #1

Po tej dawce teorii przyszła kolej na praktykę. Ogólne zasady można sformułować tak:

1. Zmontować układ pomiarowy wg schematu z rys. 3. Rezystor pomiarowy R1 powinien mieć tolerancję 1% lub lepszą. Należy pamiętać, że zbyt mała rezystancja R₁ może powodować zbyt duże obciążenie generatora. W obliczeniach nie uwzględnialiśmy jego rezystancji wyjściowej, zakładając po cichu, że jest ona bardzo mała. Trzeba jednak pamiętać, że niektóre generatory mogą mieć domyślnie ustawioną oporność wyjściową równą 50 Ω. Warto to sprawdzić przed rozpoczęciem pomiarów.

Można założyć, że rezystancja 100 Ω będzie odpowiednia dla większości przypadków. Zbyt duża może być przyczyną występowania w obwodzie trudnych do zmierzenia małych sygnałów.

2. Dołączyć kanał 1 oscyloskopu do punktu A.
3. Dołączyć kanał B oscyloskopu do punktu B.
4. Skonfigurować i uruchomić generator tak, aby wytwarzał przebieg sinusoidalny o wartości skutecznej napięcia 1 V i częstotliwości 100 Hz. Uwaga: w notach katalogowych kondensatorów najczęściej są podawane wartości ESR dla częstotliwości 100 Hz lub 1 kHz.
5. Zmierzyć wartości skuteczne mierzone w kanale 1. (U_A) i 2. (U_B).
6. Wyświetlić na ekranie przebieg będący różnicą napięć: kanał 1 – kanał 2. Kształt tego przebiegu będzie odpowiadał wykresowi prądu. Mierząc wartość skuteczną tego napięcia podzieloną przez rezystancję rezystora R₁ (np. przyjętą 100 Ω) otrzymamy wartość skuteczną prądu.
7. Zmierzyć/obliczyć przesunięcie fazowe między przebiegiem prądu (z punktu 6) a napięciem z kanału 1. Będzie to kąt φ.
8. Zmierzyć/obliczyć przesunięcie fazowe między przebiegiem z kanału 2. a napięciem z kanału 1. Będzie to kąt β.
9. Obliczyć ESR:

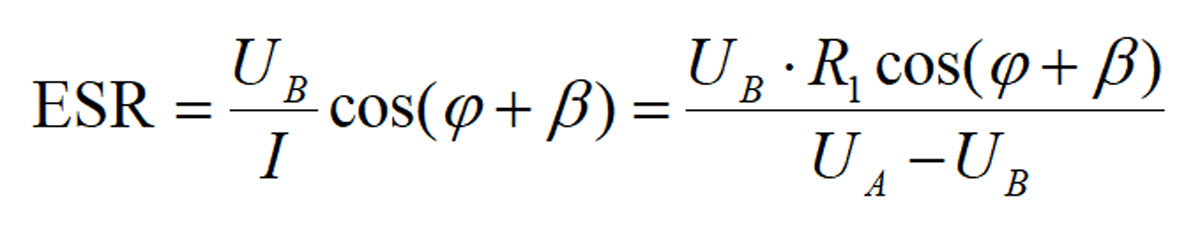
ESR jest wyrażany oczywiście w Ω (częściej w mΩ).

Słabe punkty metody

Niestety, zaproponowana metoda ma kilka wad ograniczających jej dokładność. Problemem jest pomiar niewielkich przesunięć fazowych między przebiegami i niewielkie różnice w mierzonym napięciu U_B dla dużego zakresu zmian ESR. W tab. 2 zostały zabrane przykładowe wyniki obliczeń parametrów, których należałby się spodziewać w pomiarach rzeczywistych. Przyjęto tu, że mierzony jest kondensator o pojemności 10 μF. Analizowane będą przypadki dla częstotliwości pomiarowej 100 Hz i 1000 Hz oraz dwie wartości rezystora R₁ równe 100 Ω i 1000 Ω. Obliczenia wykonano przy założeniu, że napięcie skuteczne przebiegu sinusoidalnego jest równe 1 V.

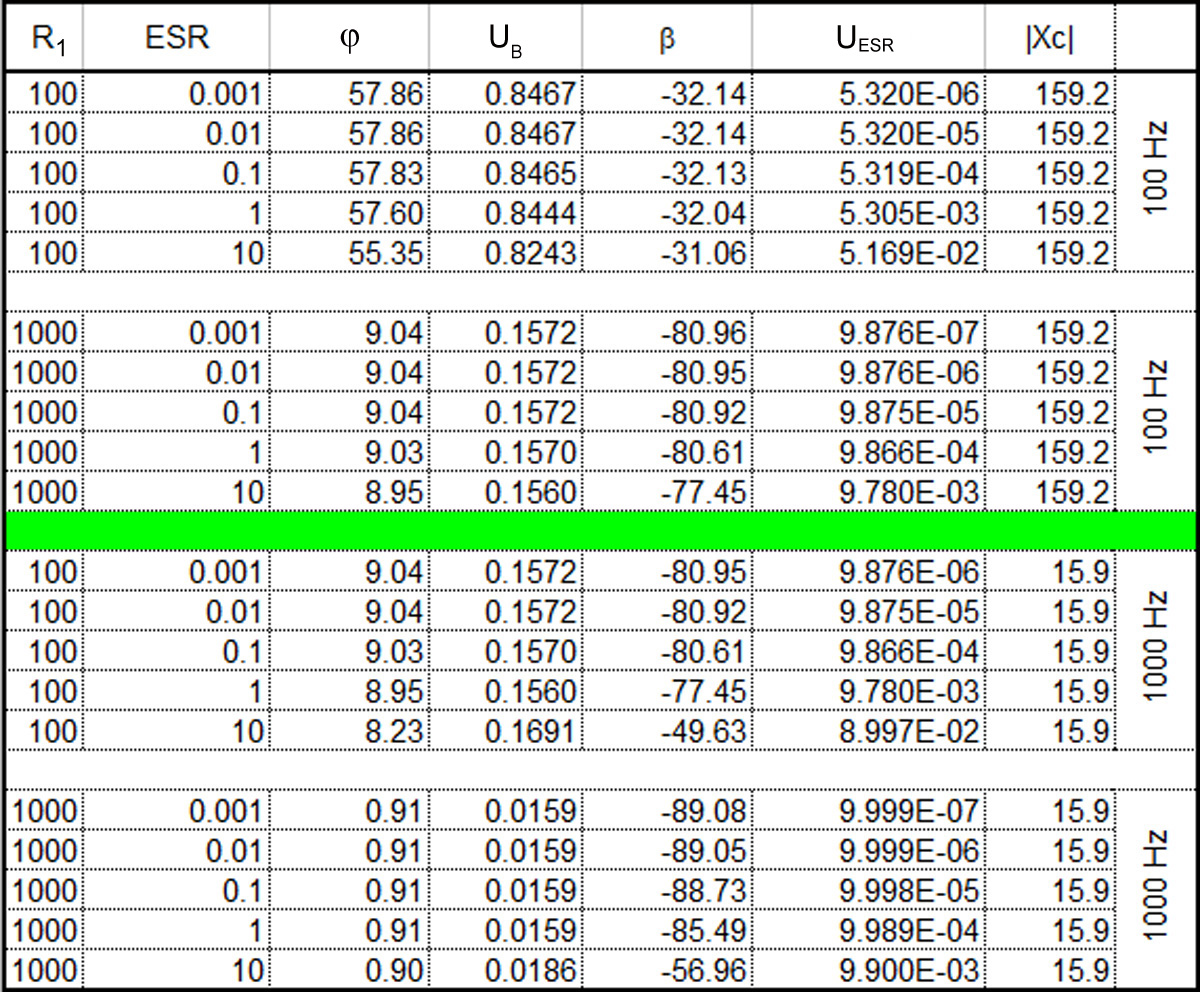
Tab. 2.

Dobrym przykładem ilustrującym problem jest przypadek, w którym został zastosowany rezystor R₁ równy 1000 Ω i wybrano częstotliwość 100 Hz. Dla tej częstotliwości reaktancja kondensatora jest równa 159,2 Ω. Jak wynika z obliczeń teoretycznych (tab. 2) przy zamianie ESR w zakresie od 1 mΩ do 1 Ω, a więc w interesującym nas przedziale, mierzone napięcie U_B jest utrzymywane na poziomie 0,157 V i w zasadzie nie zmienia się aż do czwartej cyfry znaczącej. Są to już zmiany mikrowoltowe, i poważnie można obawiać się zaburzenia wyniku przez szumy i zakłócenia. Nieco lepiej jest, gdy zostanie zastosowany rezystor R=100 Ω, ale nadal wykrycie zmian kąta β jest praktycznie niewykonalne.

Jest jeszcze jedna trudność. Układ pomiarowy jest stosunkowo prosty, można więc spodziewać się, że do jego montażu będą stosowane popularne płytki stykowe (breadboardy). Niestety, rezystancja styków, szczególnie w ich tańszych odmianach może być porównywalna z mierzonym ESR, a nawet większa od niego, zniekształcając wynik pomiaru.

Wnioski

Precyzja obliczeń przedstawionych wcześniej a służących do wykreślenia wykresu wskazowego mogła dziwić. Przecież nikt nie będzie w stanie narysować kąta z dokładnością większą niż 1º, a i to byłoby trudne. Przykładowe wyniki przedstawione w tab. 2 nieco tłumaczą takie podejście.

Jak wynika z powyższych rozważań, opisana metoda będzie raczej mało przydatna do dokładnego pomiaru ESR, ale jak już było powiedziane, zwykle nie ma takiej potrzeby. Można przyjąć, że uzyskiwane wyniki będą jako tako miarodajne dla ESR większych od 1 Ω.

Wyniki przeprowadzonych pomiarów na elementach rzeczywistych zostaną przedstawione w 2. części artykułu. Rozważymy ponadto inną metodę, która byłaby również możliwa do zastosowania w warunkach domowych.