W artykule omówiono zagadnienia związane z pseudolosowością i prawdziwą losowością w symulacjach LTspice® przy użyciu funkcji flat(), gauss() i mc(). Opisano działanie opcji „Use the clock to reseed the MC generator”, która określa metodę inicjowania generatora pseudolosowego dla funkcji MC) i jest dostępna w zakładce Hacks panelu ustawień. Omówiono kompromisy, wynikające z tego, że generator generuje liczby tylko pseudolosowe, a nie prawdziwe liczby losowe. Omówiono ponadto kompromisy związane z zagadnieniami statystycznymi, m.in. w symulacjach Monte Carlo, i bardziej ukierunkowanymi symulacjami najgorszego przypadku (Worst Case).

Wprowadzenie

Z symulacją losowości w programie LTspice® związanych jest kilka komend. Do generowania zdarzeń losowych służą funkcje takie jak: flat(), gauss() i mc().

Do symulacji rozrzutu wartości elementów pasywnych związanych z tolerancją używana jest funkcja mc(). O jej działaniu, można dowiedzieć się z pomocy programu LTspice. W tym celu należy wybrać opcję Pomoc->Pomoc LTspice (lub nacisnąć przycisk F1). Spowoduje to otwarcie podręcznika pomocy, w którym można uzyskać więcej informacji również na temat funkcji flat() i gauss().

W przykładzie z rysunku 1 funkcja mc() służy do ustawienia wartości nominalnej i tolerancji elementów R1 i C1. W przykładowej symulacji rezystancja nominalna R1 wynosi 10 kΩ, a tolerancja 5%. Funkcja mc(x,y) generuje liczby pseudolosowe o rozkładzie równomiernym między x*(1-y) a x*(1+y). W dalszej części pomocy podano więcej informacji na temat różnicy między liczbami pseudolosowymi a prawdziwie losowymi oraz omówiono metodę „zmuszenia” symulatora LTspice do generowania liczb naprawdę losowych. Dyrektywa .STEP służy do poinformowania LTspice, ile przebiegów symulacji ma być wykonanych. W poniższym przykładzie dyrektywa .STEP zmienia parametr domyślny (dummyparam) 1 na 1 do 100 w krokach co 1. Daje to 100 przebiegów symulacji, w których obie wartości R1 i C1 będą losowe.

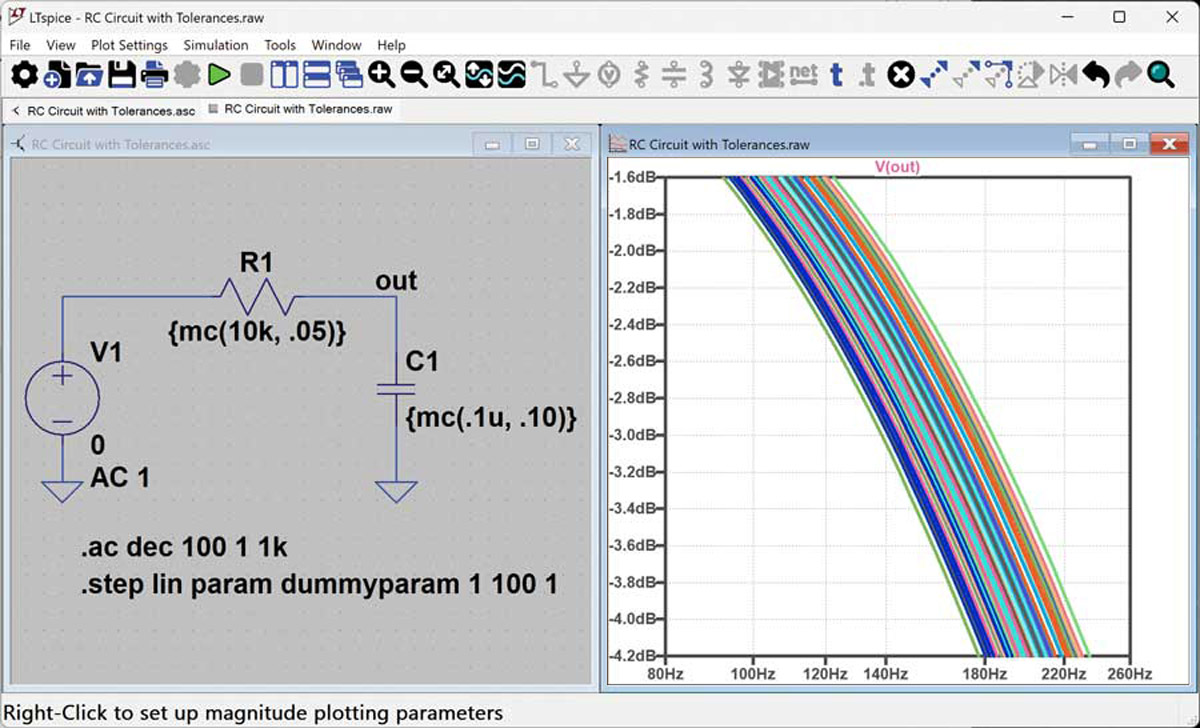
Rys. 1. Obwód RC, w którym do ustawiania wartości i tolerancji elementów pasywnych zastosowano funkcję mc()

Przyjrzyjmy się teraz, jakie wyniki będzie zwracała funkcja mc() podczas każdej iteracji. Na rysunku 2 został przedstawiony prostszy przykład, w którym zastosowane jest wyłącznie źródło napięciowe. Funkcja mc() służy tu do ustawienia napięcia nominalnego na 10 V z tolerancją 100%. Oczekujemy więc rozkładu równomiernego wartości między 0 V a 20 V. Na podstawie wyników wyświetlonych w przeglądarce przebiegów i dzienniku wyjściowym SPICE można zauważyć, że autorka uzyskała na swoim komputerze dla 10 iteracji napięcie zawierające się w przedziale od 2,7 V do 19,92 V. Trudno też osądzić, czy jest to rozkład równomierny. Większa liczba iteracji pomogłaby jednak zapewnić większą wiarygodność statystyczną wyników.

Przyjrzyjmy się temu jeszcze dokładniej i spróbujmy uruchomić tę symulację kilka razy. Czy są widoczne jakieś zmiany liczb podczas tych symulacji? Okazuje się, że za każdym razem, gdy jest uruchamiana ta symulacja, otrzymujemy takie same napięcia dla każdej iteracji. Wyniki w obrębie jednej sesji można uznać za losowe, ale pomiędzy sesjami już nie są zbyt losowe, gdyż powtarzają się identycznie w każdej z nich.

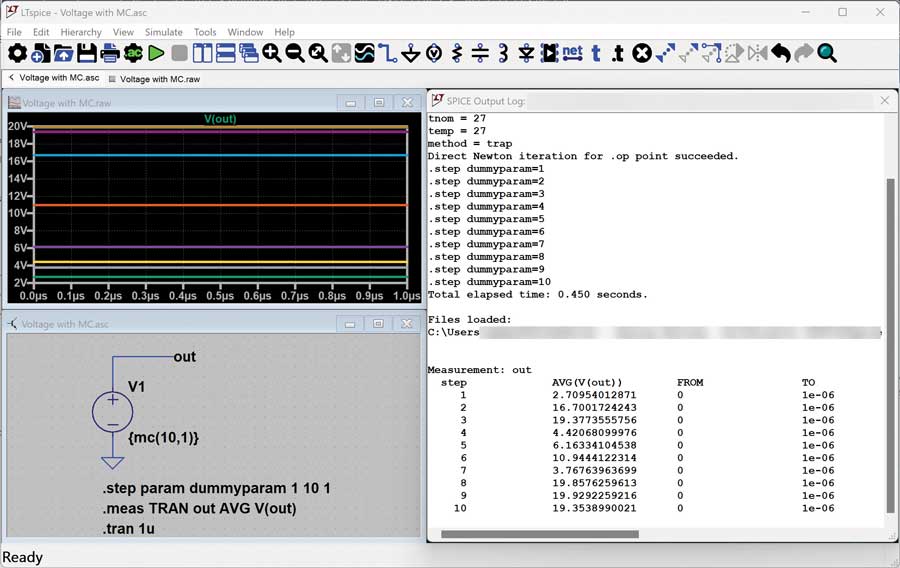
Rys. 2. Źródło napięciowe, w którym losowa wartość napięcia jest określana za pomocą funkcji mc()

Obserwujemy wartości typowe dla generowania liczb losowych przez komputer. Generatory liczb losowych w językach programowania mają powiązaną z nimi opcjonalną metodę seed(). Aby uzyskać prawdziwie losową liczbę — taką, która zmienia się przy każdym uruchomieniu programu — należy wywołać metodę seed() z wartością seed, która zmienia się przy każdym uruchomieniu. Aby uzyskać tę prawdziwą losowość, często programista przekazuje aktualny czas systemowy do metody seed().

Jak to się ma do naszej symulacji LTspice? Jeśli celem jest prawdziwa losowość między uruchomieniami w symulacji — czyli wartości, które zmieniają się podczas każdej symulacji — należy włączyć opcję „Use the clock to reseed the MC generator” (Użyj zegara do ponownego inicjowania generatora MC) w zakładce Hacks panelu ustawień (rys. 3).

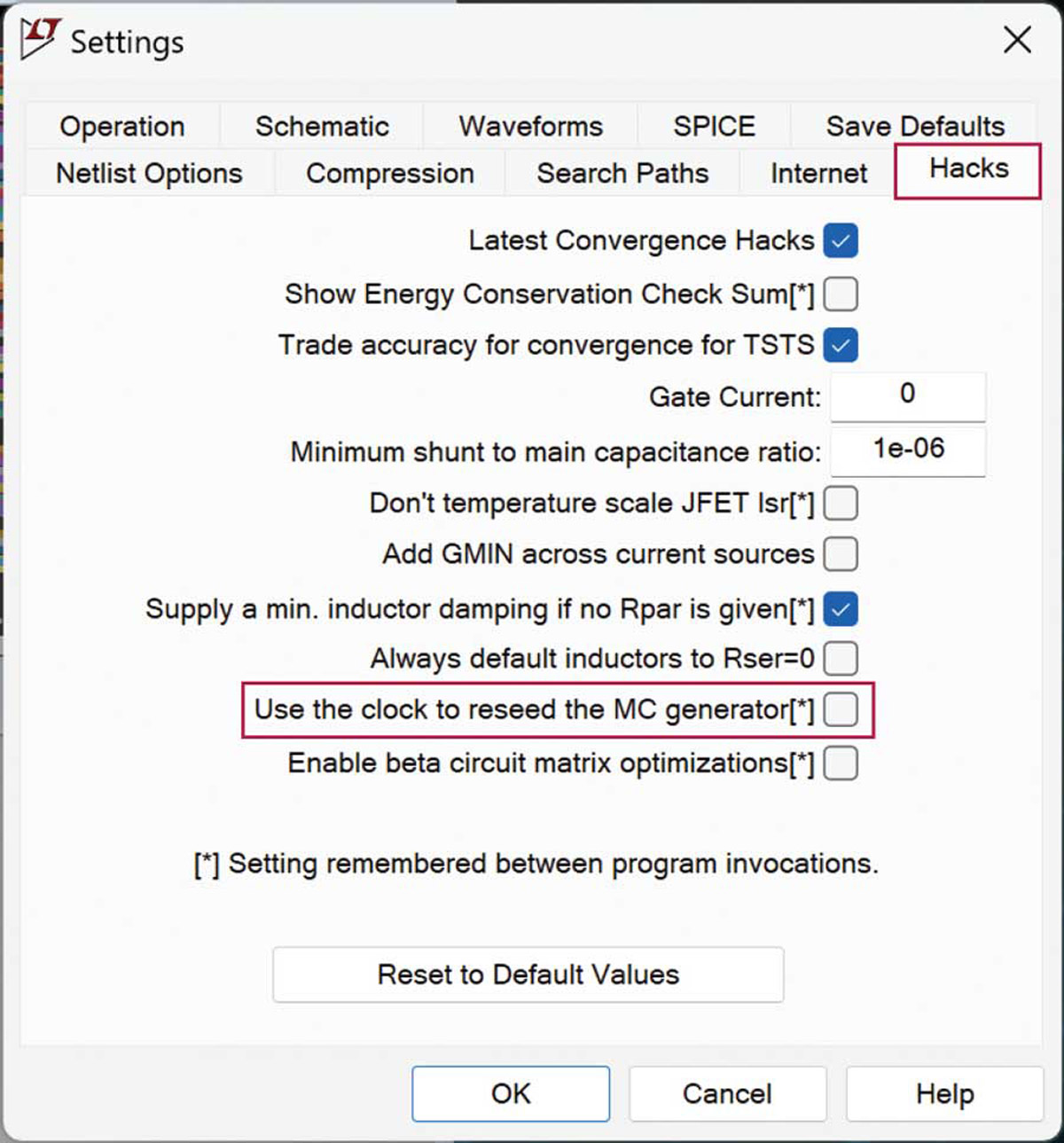
Rys. 3. Zakładka Hacks w panelu ustawień LTspice, z zaznaczonym polem włączającym losowy start generatora liczb losowych w kolejnych sesjach symulacji

Opcja „Use the clock to reseed the MC generator” działa również w przypadku funkcji flat() i gauss(). Funkcje te mogą być używane również tam, gdzie występuje funkcja mc(). Należy jednak dobrze się zastanowić, czy takiego zachowania symulacji oczekujemy. Czy chcemy, aby nasza symulacja była naprawdę losowa? Jeśli tak, stracimy przewidywalność i powtarzalność symulacji.

Aby to zilustrować, wróćmy do przykładu z rysunku 2. Co się stanie, jeśli zamierzamy symulować napięcie o rozkładzie równomiernym między 0 V a 20 V? Podany przykład nie do końca spełnia oczekiwania, ale można się do nich znacznie zbliżyć, zwiększając liczbę iteracji z 10 do 100 (rysunek 4). Ta zmiana sprawia, że symulacja znacznie bardziej zbliża się do osiągnięcia pożądanych wartości krańcowych rozkładu.

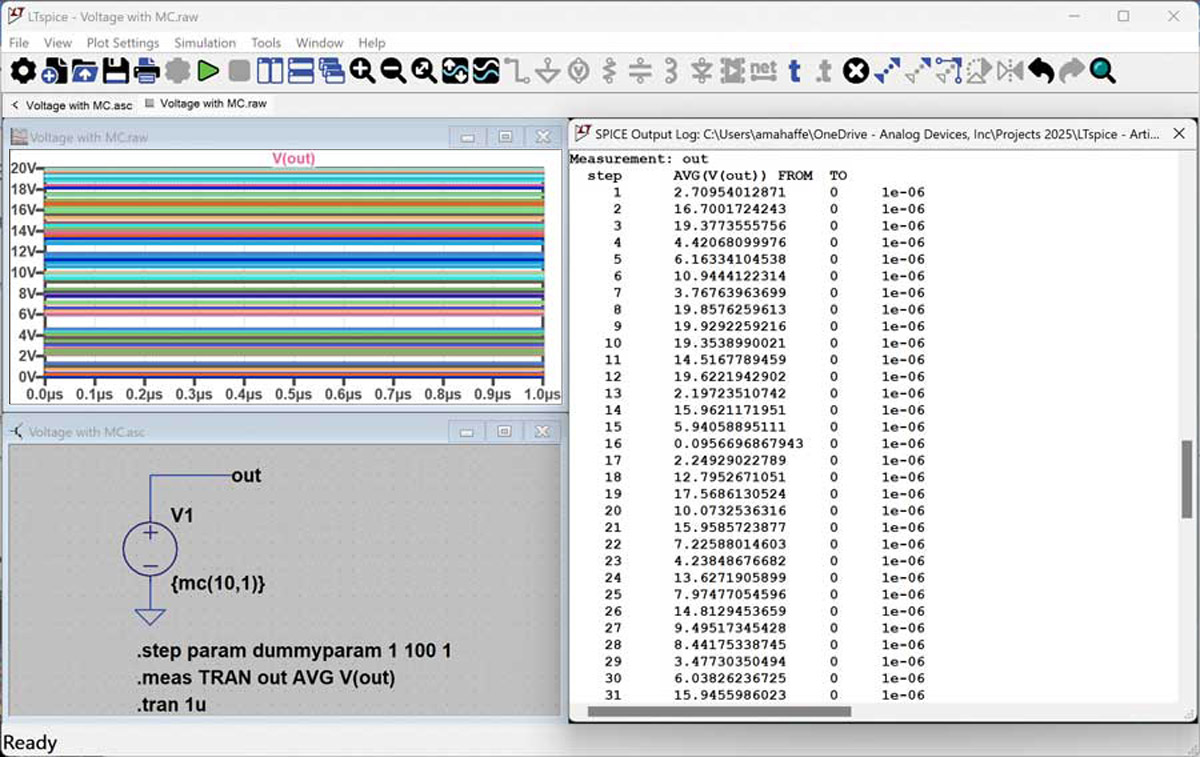
Rys. 4. Symulacja źródła napięciowego wykorzystującego funkcję mc() z większą liczbą iteracji

Teraz jest jasne, że po pierwsze: 100 iteracji mc() da całkiem dobry rozkład wartości, po drugie: bez włączenia opcji „Reseed the MC generator” w zakładce Hack wynik ten będzie powtarzalny za każdym razem, gdy zostanie uruchomiona symulacja.

Co się stanie, jeśli funkcja mc() zostanie użyta w wielu miejscach schematu? Czy można zagwarantować, że wszystkie granice tolerancji zostaną osiągnięte przy 100 iteracjach? Na rysunku 5 zilustrowano taką próbę, pokazując dwa źródła napięcia z funkcją mc() użytą do określania wartości generowanego napięcia. Wykreślając V(out1) na osi Y i jednocześnie ustawiając oś X na V(out2) widać, że kombinacje V1 i V2 osiągają dość losowy zestaw współrzędnych. Dla przypomnienia: aby zmienić wielkości wyświetlane na osi X, należy kliknąć prawym przyciskiem myszy na opis tej X i zmienić wyświetlany tekst na V(out2). Łatwo można zauważyć, że minimalne i maksymalne wartości tych napięć nie są osiągane jednocześnie, a potwierdza to brak pokrycia wykresu w punktach granicznych.

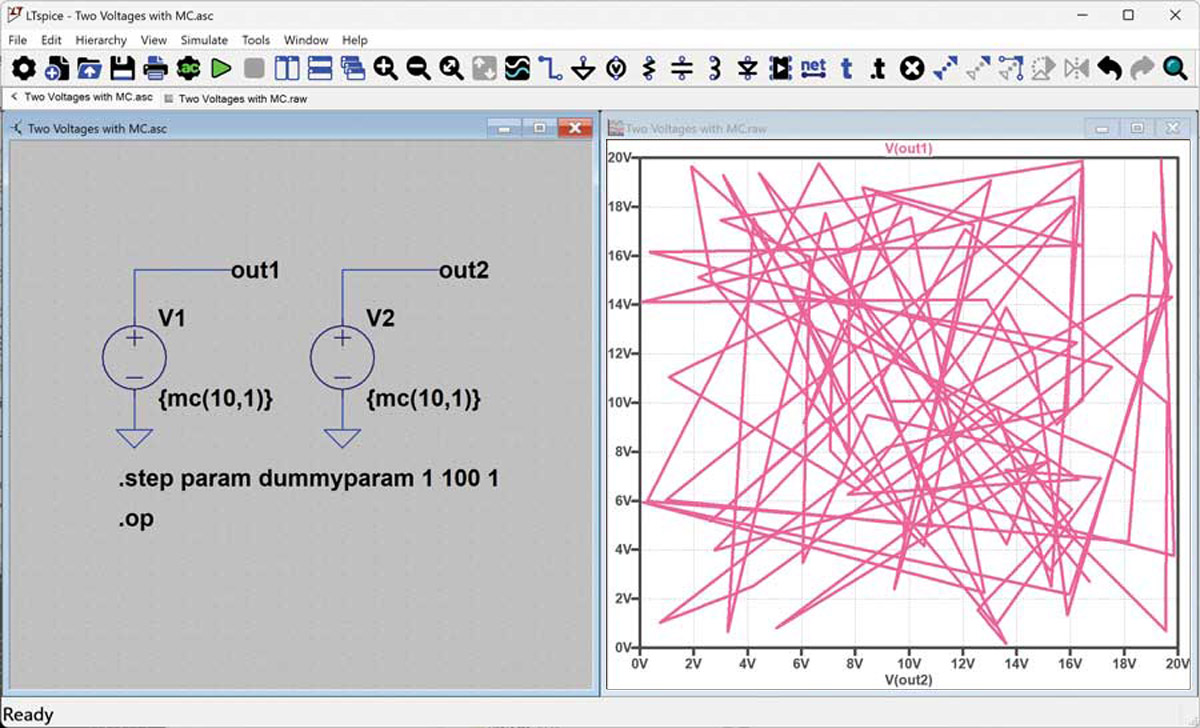
Rys. 5. Wykres wyników dwóch napięć mc() w jednej symulacji

Jeśli chcemy uzyskać pełniejsze pokrycie, konieczne jest wykonanie większej liczby iteracji (rys. 6).

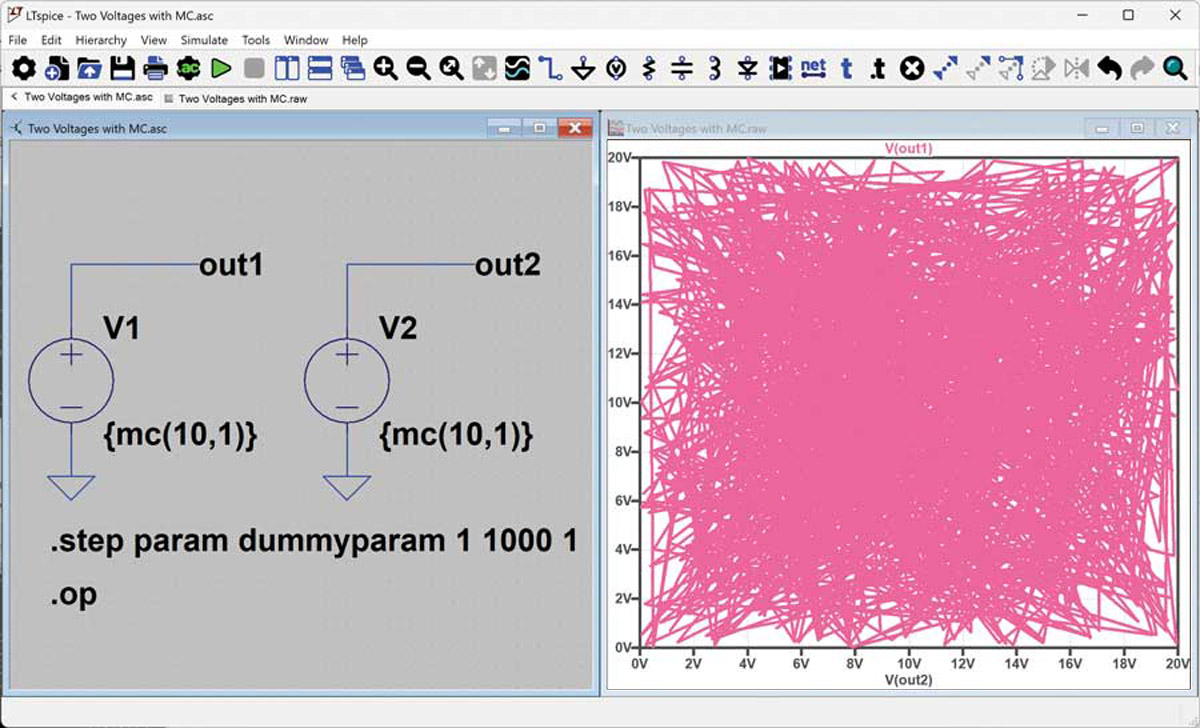
Rys. 6. Wykres wyników z większą liczbą iteracji

W tym prostym przykładzie symulacja przebiega szybko, więc nie ma przeszkód, aby przeprowadzić ją nawet 1000 razy. Co jednak w przypadku, gdy symulacja trwa długo i przeprowadzenie jej z taką liczbą iteracji zajęłoby godziny (lub dni)? Rozważmy również potencjalną wartość włączenia opcji „Use the clock to reseed the MC generator”. Jeśli uznamy, że wartości generowane przez mc() w przebiegu symulacji są zadowalające, czy celem jest powtarzalność tych wyników w kolejnych przebiegach? A może wolimy, aby zmieniały się one losowo między przebiegami symulacji? Jest to ważne pytanie, które należy rozważyć przed włączeniem tego ustawienia.

Przyjrzyjmy się mniej losowemu podejściu, które jednak znacznie skróci czas symulacji.

Na rysunku 7 przedstawiono przykład zapewniający, że symulacja uwzględnia wszystkie granice tolerancji elementów pasywnych, przy jednoczesnym zachowaniu minimalnego czasu symulacji. W tym przykładzie przechodzimy przez trzy wartości R1 i trzy wartości C1, co daje dziewięć przebiegów symulacji i zapewnia uwzględnienie scenariuszy dla jednoczesnych wartości minimalnych (lub maksymalnych) elementów.

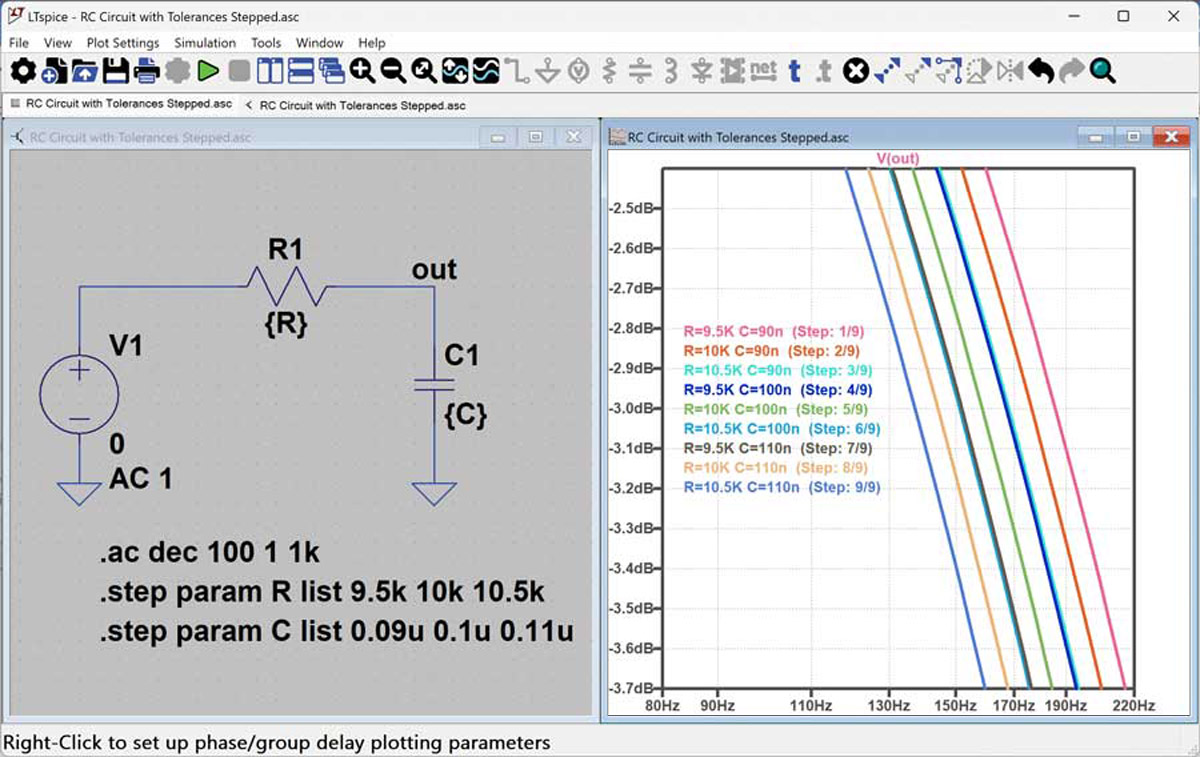
Rys. 7. Symulacja z nominalnymi i skrajnymi wartościami elementów R i C wynikającymi z ich tolerancji

Wnioski

Jeśli celem jest zbadanie układu w różnych warunkach pracy, bardziej sensowne może być podejście, w którym losowość ma mniejsze znaczenie. Jeśli natomiast celem jest przeprowadzenie analizy statystycznej podczas symulacji w różnych warunkach, najlepszym rozwiązaniem może być zastosowanie dużej liczby iteracji symulacji w połączeniu z funkcjami wprowadzającymi losowość.

Więcej informacji na temat zdarzeń losowych można uzyskać w artykule „How to Model Statistical Tolerance Analysis for Complex Circuits Using LTspice”.

Opracowanie Jarosław Doliński