Tajemnica pierwiastka z 6 i liczby 29, czyli generatory z przesuwnikiem fazy CR
Generatory stanowią wydzielony dział podstaw elektroniki, przez który musi przejść każdy przyszły inżynier. Co więcej, nie jest to dział łatwy do opanowania, a to głównie ze względu na dużą liczbę różnych konfiguracji tego typu urządzeń. I – jak na ironię – jest tak, mimo że cała teoria generatorów jest oparta w zasadzie na jednym, względnie prostym kryterium określającym dwa warunki powstania drgań w obwodzie. My nie będziemy tu bardzo głęboko wchodzić w ogólną teorię, aczkolwiek matematyki będzie sporo. Będzie ona jednak skoncentrowana na wybranym typie generatora. Postanowiłem dość szczegółowo przedstawić matematyczną stronę zagadnienia, gdyż w dużej części publikacji na ten temat pojawiają się różne dziwne wzory matematyczne, zawierające tajemnicze czynniki, które nie wiadomo skąd się wzięły, a czytelnicy muszą przyjmować je na wiarę. W zasadzie, do konstruowania urządzeń dokładna wiedza teoretyczna nie jest potrzebna, jeśli ktoś wcześniej ją już rozpoznał i przedstawił w skondensowanej postaci, np. właśnie jako wzory matematyczne. Spora grupa konstruktorów zapewne lubi jednak znać szczegóły i wiedzieć, skąd wzięły się poszczególne czynniki w takich wzorach.
Teoria minimum minimorum
Wróćmy do zakresu wiedzy, który jest niezbędny do tego, by móc konstruować generatory. Jak już było powiedziane, do wzbudzenia drgań obwodzie ze sprzężeniem zwrotnym muszą być spełnione dwa warunki ogólnie znane jako warunek Barkhausena, Są to:
- warunek fazy
- warunek amplitudy.
Warunek fazy określa całkowite przesunięcie fazy w układzie z pętlą sprzężenia zwrotnego, które musi być równe 360° (lub wielokrotność tej wartości, ze szczególnym przypadkiem 0°).
Z warunku amplitudy wynika, że całkowite wzmocnienie z pętlą sprzężenia zwrotnego musi być równe 1.
I to wszystko. Jak widać, nie ma powodu do paniki. Praktyka bywa jednak zaskakująco złośliwa. Konstruktorzy muszą często nieźle się napracować, aby ich generator choćby się wzbudził, nie mówiąc o tym, by częstotliwość drgań była zgodna z zakładaną. Natomiast akustycy sporo by dali za to, by ich wzmacniacze nie wydawały przeraźliwych dźwięków po włączeniu. Czasami obserwują też dziwne grzanie się tranzystorów końcowych stopni wzmacniacza, jakby pracowały z pełną mocą. Dopiero po dołączeniu oscyloskopu okazuje się, że wzmacniacz stał się generatorem sygnałów ultradźwiękowych.
Generator z przesuwnikiem fazy CR – dalszy ciąg teorii
Generatory z przesuwnikiem fazy mogą być budowane z użyciem tranzystorów lub wzmacniaczy operacyjnych. My rozpatrzymy konstrukcję opartą na wzmacniaczu operacyjnym pracującym w konfiguracji z wejściem odwracającym. Taki wzmacniacz przesuwa fazę sygnału o 180°, zatem aby zapewnić warunek fazy potrzebny do wzbudzenia drgań, należy zaprojektować obwód sprzężenia zwrotnego, który przesunie fazę o kolejne 180°. Od razu do głowy przychodzi pomysł zastosowania prostego przesuwnika zbudowanego na elementach C i R. Teoretycznie jedno takie ogniwo może przesunąć fazę maksymalnie o 90°, ale jest to wartość asymptotyczna niemożliwa do osiągnięcia w praktyce. Dlatego, do generatora należy użyć co najmniej 3 takich ogniw, i w rozwiązaniach praktycznych najczęściej spotykamy właśnie takie konstrukcje. Do rozstrzygnięcia pozostaje jeszcze decyzja, czy ma to być ogniwo C-R czy R-C. I znowu, teoretycznie niema to znaczenia, jednak w praktyce korzystniej jest użyć konfiguracji C-R (kondensator na wejściu, rezystor do masy) i chyba częściej jest ona spotykana w praktyce. Po zastosowaniu trzech takich przesuwników połączonych kaskadowo, na pewno dla określonej częstotliwości uzyskamy przesunięcie fazy o pożądane 180°. Ale dla jakiej?
Zanim przejdziemy do rozważań teoretycznych, należy się jedno wyjaśnienie. Otóż w przypadku generatorów z przesuwnikiem fazy złożonym z elementów R i C, w literaturze często spotykamy ogólną nazwę – generatory RC, bez względu na kolejność występowania tych elementów w przesuwniku fazy. Nie są to jednak konfiguracje tożsame – stosując te same wartości elementów R i C otrzymamy zupełnie inne częstotliwości generowanych przebiegów. Aby podkreślić kolejność występowania elementów w przesuwniku fazy stosuję nazewnictwo „generatory CR”, a nie RC.
Wracamy do naszego generatora CR. I tu zaczyna się problem z wiedzą dostarczaną w publikacjach. Bez problemu znajdziemy informację o tym, że jeśli w każdym stopniu zastosujemy identyczne rezystancje rezystorów i identyczne pojemności kondensatorów, to przesunięcie fazy o 180° uzyskamy dla częstotliwości:
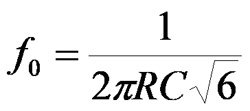
a wzmocnienie wzmacniacza musi wynosić 29 V/V. No i fajnie, tylko o ile czynnik 2πRC wygląda znajomo, to skąd u licha wzięły się te dziwne liczby: √6 i 29? Spróbujemy to wyjaśnić, ale bez matematyki się nie obędzie.
Teoria obwodów i rozwiązywanie układu równań na tropie √6 i 29
Aby rozwiązać zagadkę tajemniczych liczb, należy obliczyć transmitancję czwórnika składającego się z 3 połączonych kaskadowo elementów CR (rys. 1). Układ ten będzie pełnił funkcję przesuwnika fazy o 180°. Trzeba tylko pamiętać, że jego wejście znajduje się na tym rysunku z lewej strony, a w docelowym układzie będzie z prawej strony, ponieważ będzie on pełnić funkcję bloku sprzężenia zwrotnego.
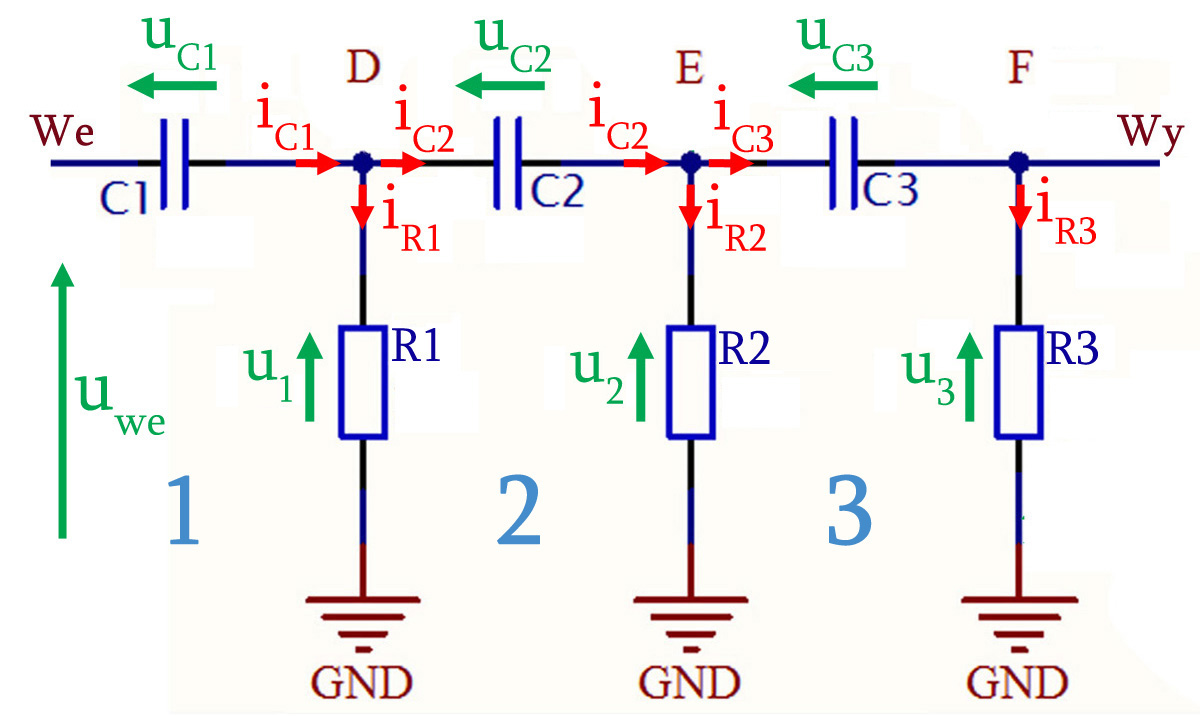
Rys. 1. Przesuwnik fazy składający się z 3 połączonych kaskadowo elementów C-R
Idąc na skróty można by było policzyć transmitancję jednego członu CR tego złożonego przesuwnika fazy i biorąc pod uwagę, że jest to połączenie kaskadowe jako wynik końcowy podać transmitancję jednego stopnia podniesioną do potęgi 3. Byłoby to jednak słuszne tylko przy założeniu, że każdy następny stopień nie obciąża poprzedniego, a w tym przypadku tak nie jest. Liczymy więc dokładnie. Na rysunku 1 uwzględniono strzałkowanie napięć i prądów potrzebne do prawidłowego sformułowania wyrażeń matematycznych opisujących układ. Wyróżniamy w nim 3 oczka i 3 węzły, co pozwoli napisać układ 6 równań z 6 niewiadomymi, który docelowo powinien zredukować się do układu 3 równań z 3 niewiadomymi. Trzeba będzie przejść jakoś przez te męki, mimo że do obliczenia transmitancji całego przesuwnika wystarczy tylko jedno równanie. Zaczynamy. Najpierw układamy 3 równania opisujące napięcia w kolejnych trzech oczkach (1…3). Następnie to samo zrobimy z węzłami opisującymi rozpływ prądu w każdym z kolejnych węzłów (D, E, F). Otrzymujemy układ równań:
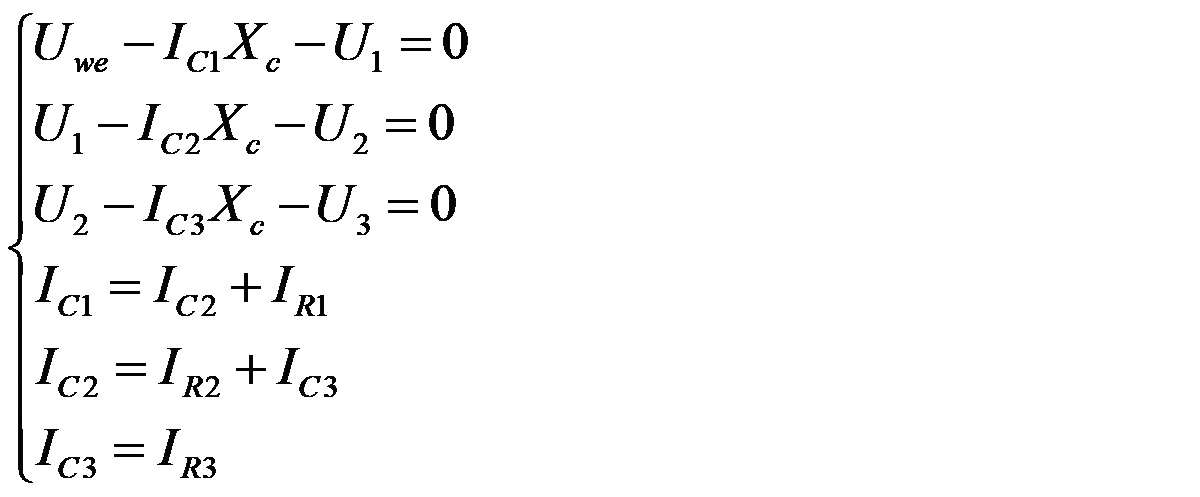
W równaniach tych elementom C i R zostały przydzielone indeksy, mimo że mają one odpowiednio równe wartości (R1=R2=R3=R, C1=C2=C3=C). Dzięki temu można łatwo zorientować się, do których elementów układu odnoszą się poszczególne równania. Ponadto, symbol X oznacza reaktancję kondensatora. Prądy płynące przez poszczególne rezystory są łatwe do obliczenia:
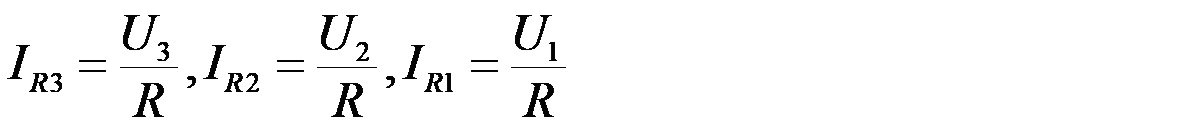
Mając te dane można policzyć prądy płynące przez kondensatory:
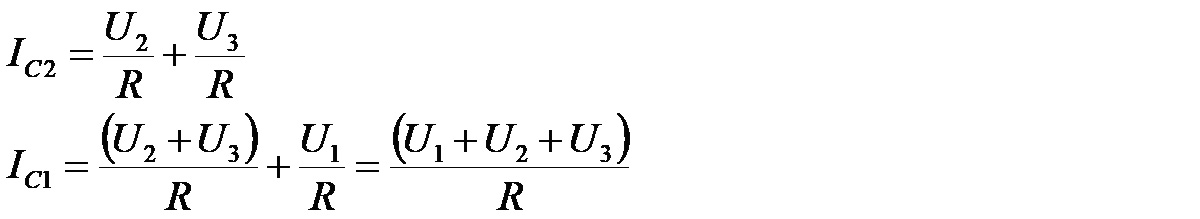
Teraz uwzględniając, że X=1/sC, a także podstawiając powyższe zależności do równań opisujących napięcia, zaczynając od trzeciego i podążając w górę, otrzymujemy:
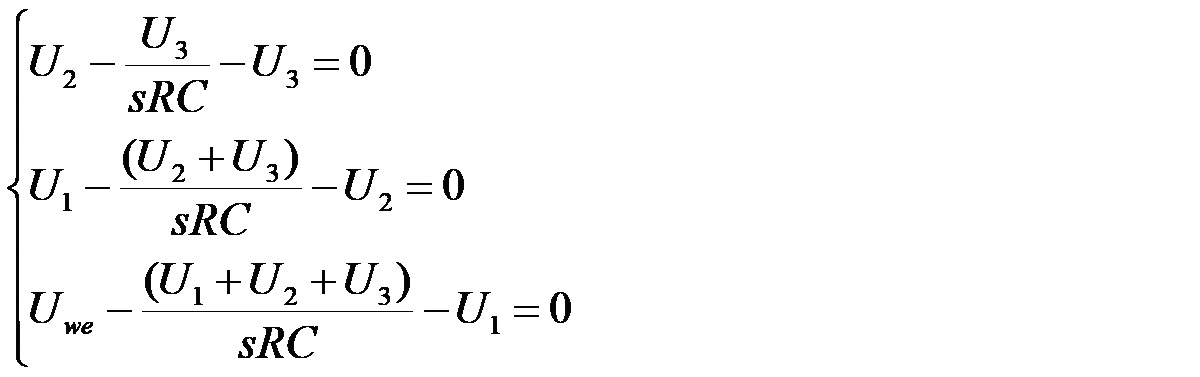
A po wymnożeniu każdego z tych równań przez sRC otrzymujemy:
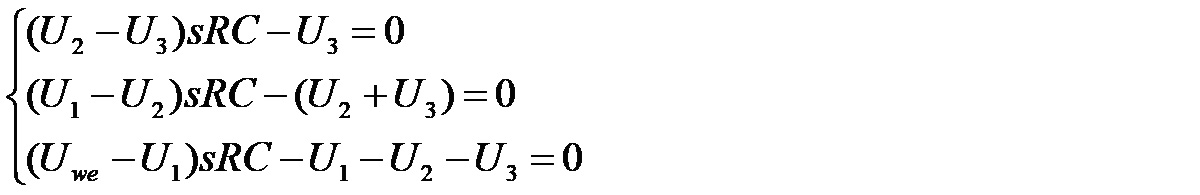
W ten sposób otrzymaliśmy wspomniany wcześniej układ 3 równań z 3 niewiadomymi: U1, U2 i U3. Uwe jest wartością znaną, od niej zależą wartości pozostałych napięć. Pozostaje więc jedynie rozwiązanie tego układu równań, ale jako że jest to już zadanie dość trywialne, zostaną podane jedynie wyniki, a w zasadzie jeden wynik dla napięcia U3. Otóż napięcie to jest równe:
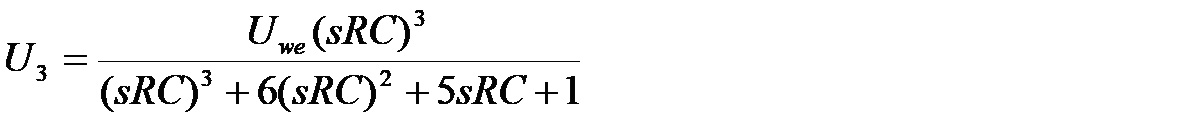
Od tego równania do interesującej nas formuły opisującej transmitancję całego układu przesuwnika już tylko krok, ponieważ transmitancja opisuje stosunek napięcia wyjściowego do wejściowego. Jak można zauważyć napięcie U3 jest właśnie napięciem wyjściowym. Transmitancja jest więc równa:
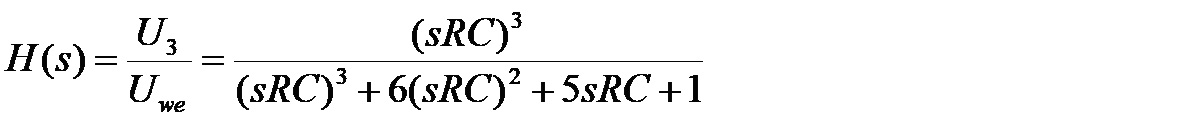
W obliczeniach zastosowany był rachunek operatorowy. Do policzenia charakterystyki częstotliwościowej konieczne jest podstawieniu s=jω. Przyjmując, że RC=τ, transmitancja przybiera teraz postać:
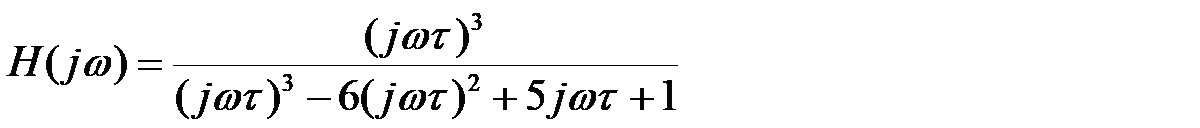
czyli po uporządkowaniu ostatecznie:
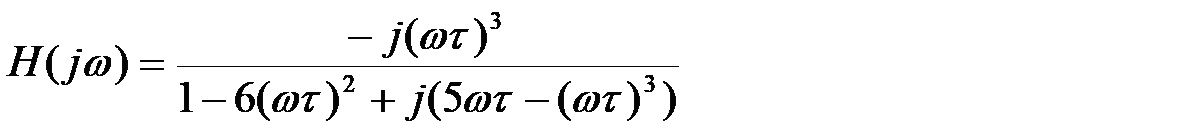
W liczniku występuje tylko ujemna liczba urojona, więc będzie on wnosił przesunięcie -90°. My potrzebujemy przesunięcia 180° (dla którego znak nie ma znaczenia), więc czynnik znajdujący się w mianowniku musi wnosić przesunięcie +90°. Znak + wynika z tego, że łączne przesunięcie fazy to przesunięcie licznika minus przesunięcie mianownika. Żeby był spełniony ten warunek, część rzeczywista mianownika, czyli składnik 1-6(ωτ)2, musi być równy 0, a to zachodzi, gdy:

Jak widać, jesteśmy już o krok od rozwiązania problemu z tajemniczym ∨6, bo z powyższego równania otrzymujemy:

a więc
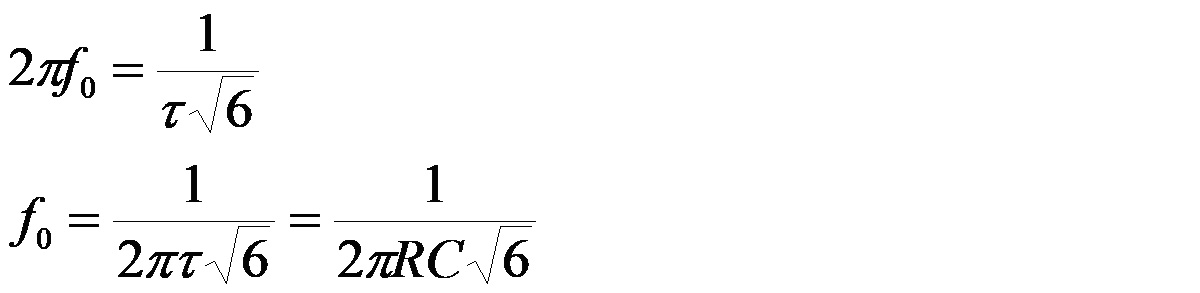
OK. Pierwiastek z 6 mamy ogarnięty, teraz kolej na odpowiedź, dlaczego wzmocnienie musi być równe 29. Wymagane przesunięcie fazowe 180° jest osiągane kosztem znacznego tłumienia sygnału. Nasz przesuwnik fazy, to jednocześnie układ filtra górnoprzepustowego, a my pracujemy na dość stromym zboczu (60 db/dek) jego charakterystyki częstotliwościowej. Aby odpowiedzieć na nurtujące nas pytanie, jak bardzo będzie stłumiony sygnał wejściowy dla częstotliwości dającej przesunięcie o 180°, należy więc policzyć moduł transmitancji dla częstotliwości f0. Moduł transmitancji jest równy modułowi licznika podzielonemu przez moduł mianownika. Mamy zatem:
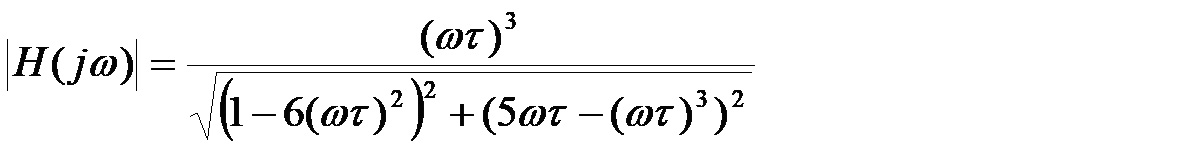
Jeśli teraz przyjmiemy, że:
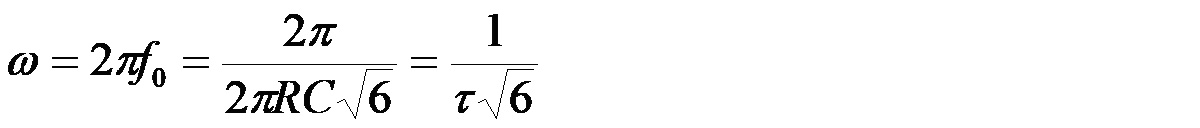
czyli

i ten czynnik podstawimy do wzoru na moduł transmitancji, to uzyskamy:
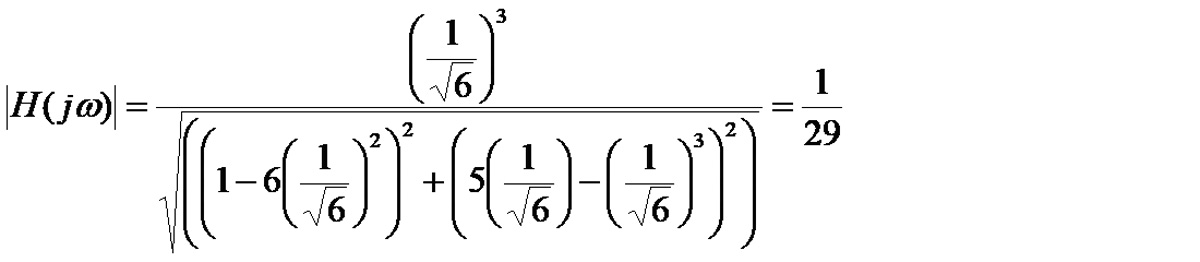
Mamy więc i tajemniczą liczbę 29. Z powyższej zależności wynika, że dla częstotliwości f0, przy której układ przesuwa fazę sygnału wejściowego o 180° następuje jednocześnie jego 29-krotne stłumienie. A jak pamiętamy, z warunku amplitudy wynika, że do powstania drgań w układzie ze sprzężeniem zwrotnym wzmocnienie powinno być równe 1. Skompensowanie strat wnoszonych przez układ przesuwający fazę wymaga, aby wzmacniacz miał wzmocnienie równe 29 V/V. Jeśli wzmocnienie to będzie zbyt małe, drgania nawet jeśli powstaną, zostaną szybko stłumione, natomiast przy zbyt dużym wzmocnieniu wzmacniacz zostanie przesterowany, powstaną spore zniekształcenia i w widmie pojawi się sporo harmonicznych.
Na zakończenie rozważań teoretycznych warto jeszcze wspomnieć, co by się stało, gdybyśmy zamiast obliczeń dokładnych zastosowali uproszczoną formułę określającą transmitancję całego przesuwnika, jako podniesioną do trzeciej potęgi transmitancję pojedynczego ogniwa. Tu jednak oszczędzę męczarni matematycznych i podam gotowy wynik. Otóż przy powyższym założeniu częstotliwość f0 byłaby √2 razy większa od wartości prawidłowej.
Symulacja
Zanim zabierzemy się do montażu generatora, sprawdźmy na wszelki wypadek czy ma on szansę działać. Użyjemy do tego celu programu LTspice. W rozwiązaniu praktycznym przewiduję zastosowanie popularnego wzmacniacza operacyjnego TL084, który zasilimy napięciami +5 V i -5 V. Do symulacji konieczne będzie pobranie modelu układu TL084 i dołączenie go do plików symulacji. Najpierw jednak sprawdzimy sam 3-stopniowy przesuwnik fazy składający się z ogniw CR. Na rysunku 2 pokazano schemat symulowanego przesuwnika wraz z kilkoma komendami obliczającymi niektóre parametry tego układu. Nas będą interesować szczególnie przesunięcia fazowe w poszczególnych punktach.
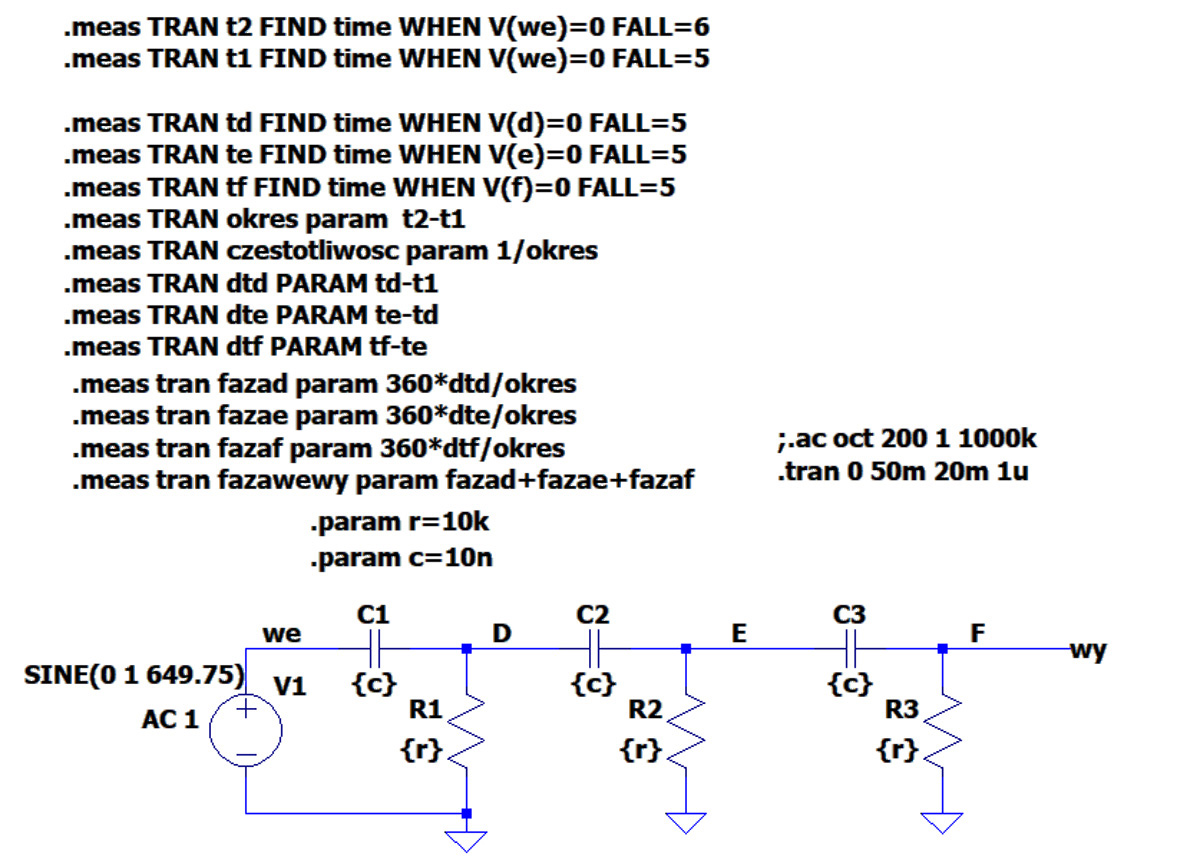
Rys. 2. Schemat przesuwnika fazy zastosowany do symulacji w programie LTspice
Na rysunku 3 obserwujemy przebiegi napięć w kolejnych węzłach układu zaczynając od źródła. Częstotliwość sygnału wejściowego jest równa 649,75 Hz, a więc odpowiada obliczonej częstotliwości f0 dla układu z elementami R=10 kW, C=10 nF. Jak widać z uzyskanego wykresu sygnał na wyjściu (w węźle F) jest rzeczywiście odwrócony o 180° względem wejścia. Potwierdzają to również automatyczne obliczenia z okna „Spice Error Log” pokazane na rysunku 4.
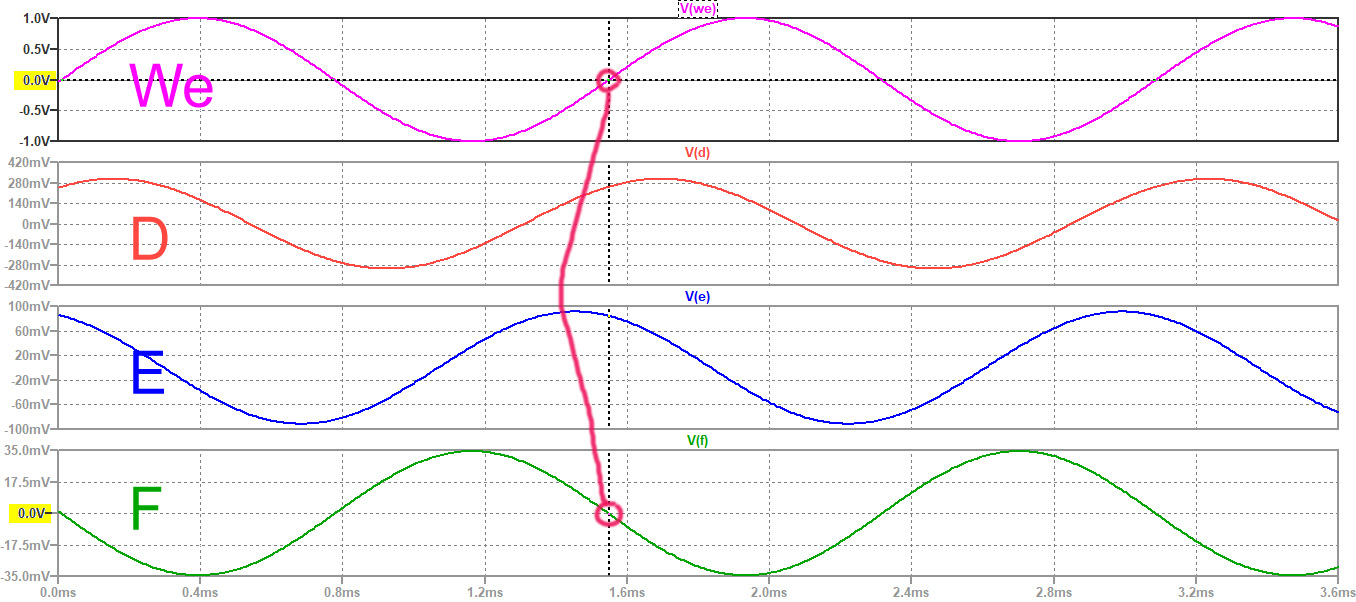
Rys. 3. Wykres napięć w kolejnych węzłach przesuwnika fazy
Drobne odchyłki od oczekiwanych wartości wynikają z ograniczonego kroku symulacji oraz błędów zaokrągleń. Należy zauważyć, że skalowanie osi pionowych jest różne dla każdego przebiegu, co zostało podyktowane chęcią zwiększenia czytelności wykresów. Wygląda na to, że wyniki symulacji zgodziły się z obliczeniami.
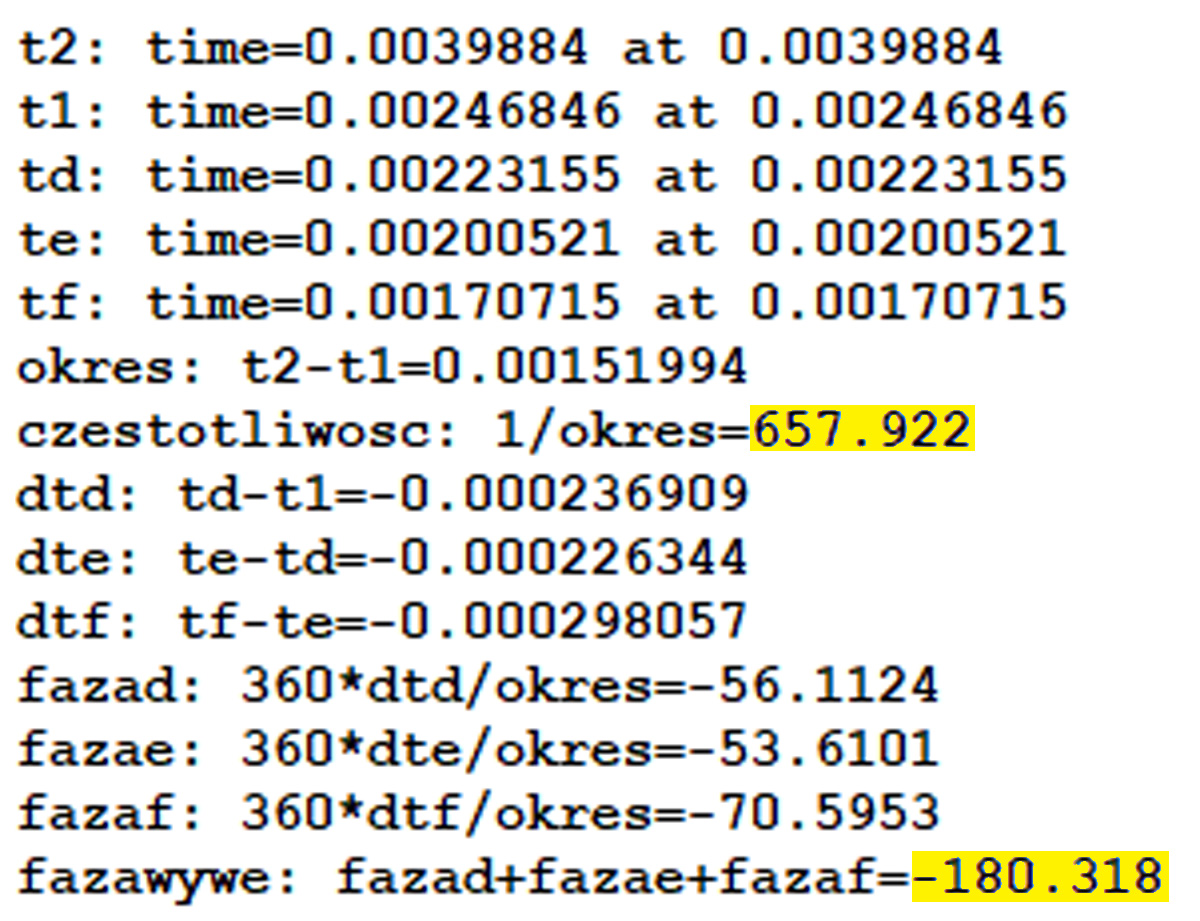
Rys. 4. Okno „Spice Error Log” z obliczonymi przesunięciami fazy w poszczególnych węzłach układu
Należy jeszcze zbadać, czy układ z powyższym przesuwnikiem fazy włączonym w pętlę sprzężenia zwrotnego wzmacniacza operacyjnego pracującego w konfiguracji z wejściem odwracającym będzie generował jakiś przebieg (jaki?) i czy będzie on choćby mniej więcej zgodny z obliczeniami i przewidywaniami.
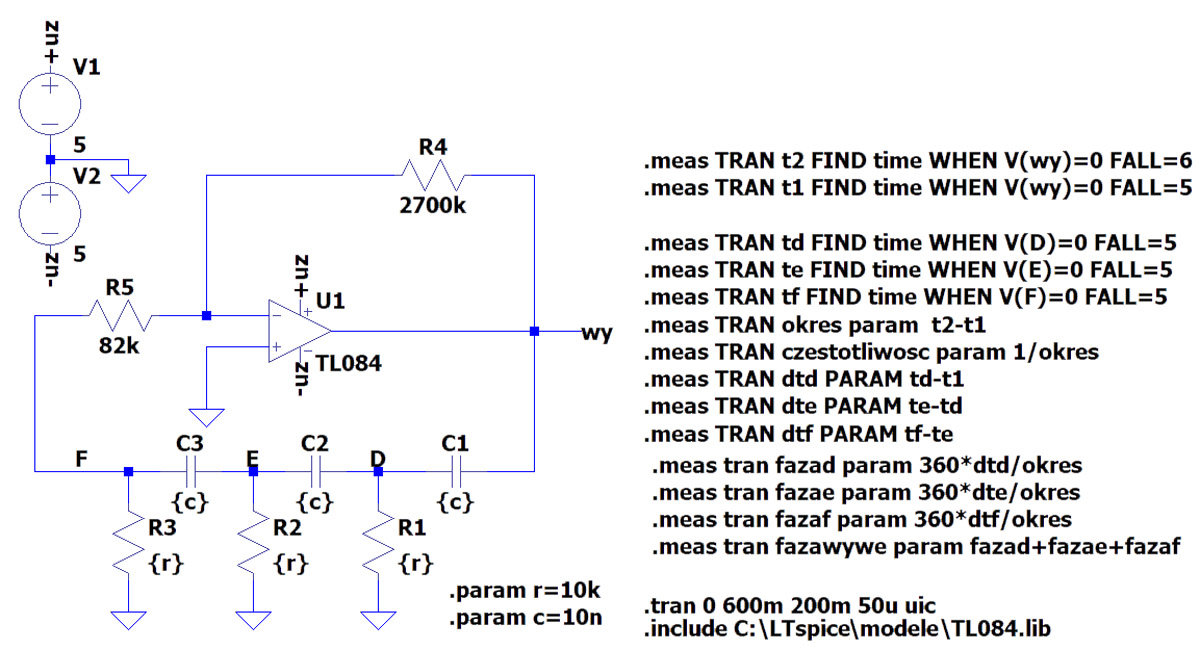
Rys. 5. Schemat generatora użyty do symulacji
Schemat symulowanego generatora zamieszczono na rysunku 5. Rezystory R4 i R5 ustalają wzmocnienie wzmacniacza, tak więc wzmocnienie to wynosi: Ku=-R4/R5=-32,9 V/V. Znak minus oznacza odwrócenie fazy, a wartość 32 jest nieznacznie większa od wymaganych 29, co wynika z dopasowania do wartości elementów z szeregu co najmniej 10-procentowego (E12). Poza tym, niewielki margines zapewni nam jako taką pewność, że generator wzbudzi się. I, jak się po uruchomieniu symulacji okazuje, układ faktycznie generuje drgania przedstawione na rysunku 6.
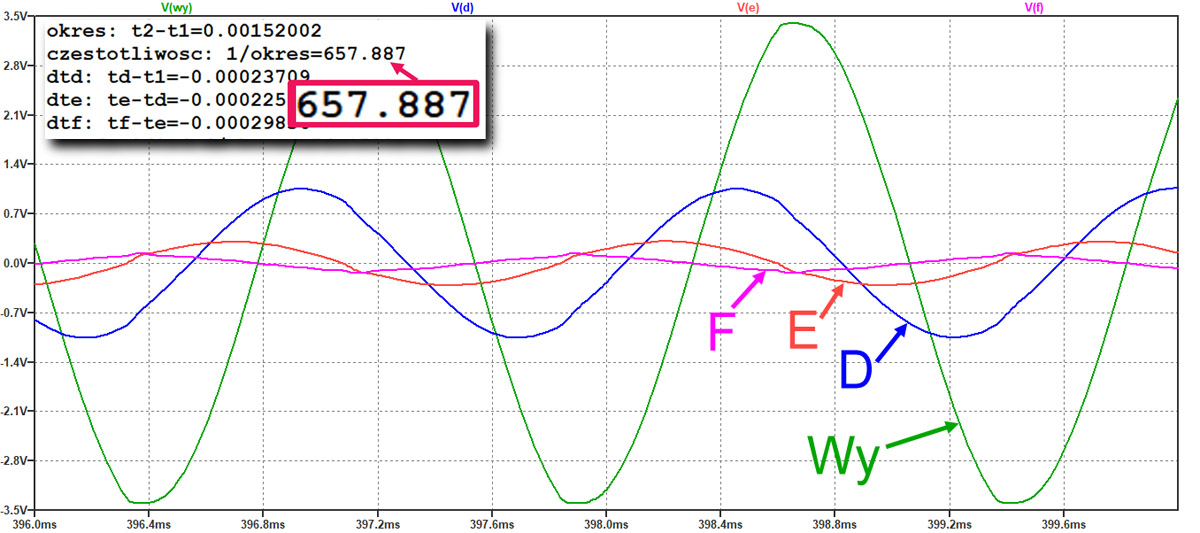
Rys. 6. Przebiegi w różnych punktach symulowanego generatora
Jak widać, częstotliwość drgań nieco różni się od wyliczonej wcześniej dla przesuwnika fazy f0,=649,75 Hz. Częstotliwość drgań symulowanego generatora wynosi 657,9 Hz, co wynika z obciążenia przesuwnika impedancją wejściową wzmacniacza powodującą znaczne zniekształcenie napięcia w węźle wyjściowym F przesuwnika fazy. Wszystkie napięcia z poszczególnych węzłów zostały pokazane na jednym wykresie (rys. 7), przy czym nie zachowano tu jednakowego skalowania osi pionowych w poszczególnych panelach.
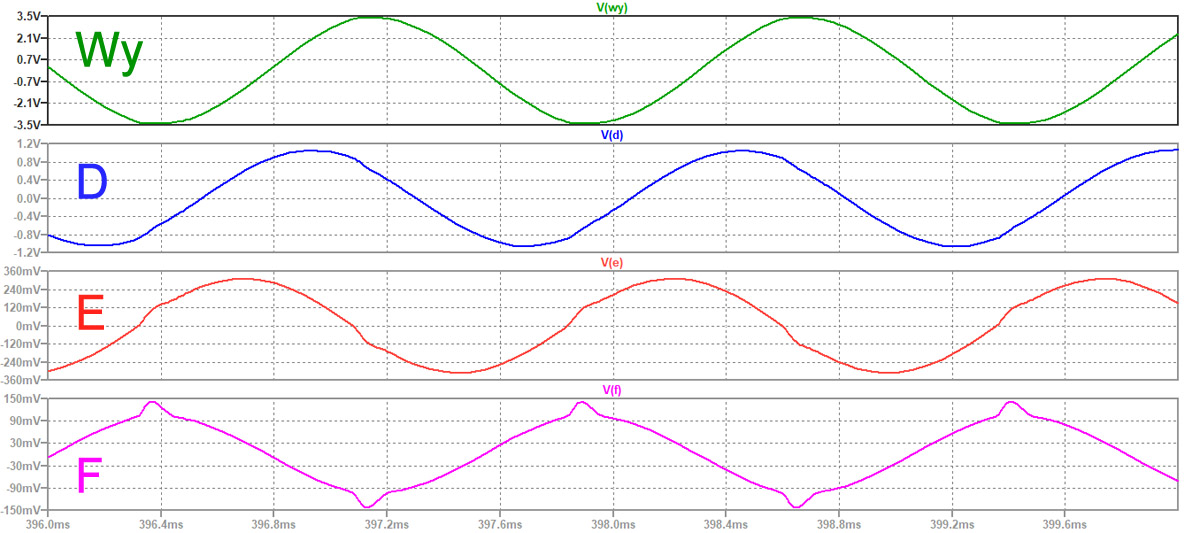
Rys. 7. Porównanie przebiegów z różnych węzłów przesuwnika fazy zastosowanego w generatorze z indywidualnym skalowaniem wykresów
Na zakończenie rozważań teoretycznych warto jeszcze zauważyć, że mimo zastosowania napięć zasilających ±5 V, amplituda generowanego sygnału nie przekracza 3,5 V. Wynika to z faktu, że układ TL084 nie jest wzmacniaczem rail-to-rail.
Mimo drobnych odchyłek od obliczeń, można jednak uznać, że wyniki symulacji z inżynierską precyzją spełniły oczekiwania. A jak będzie z pomiarami układu rzeczywistego?
Materiały
- Uniwersalny zestaw pomiarowy Analog Discovery 2
- Stykowa płytka prototypowa
- Przewody połączeniowe
- Wzmacniacz operacyjny TL084
- Rezystor 10 kΩ – 3 szt.
- Rezystor 82 kΩ
- Rezystor 2,7 MΩ
- Kondensator 10 nF – 3 szt.
Instrukcja do ćwiczenia i przebieg ćwiczenia
Zmontuj na płytce stykowej układ generatora według rysunku 8. W zielonych kółkach zaznaczono wyprowadzenia zestawu Analog Discovery 2, a strzałkami zaznaczono punkty schematu, do których powinny być dołączone.
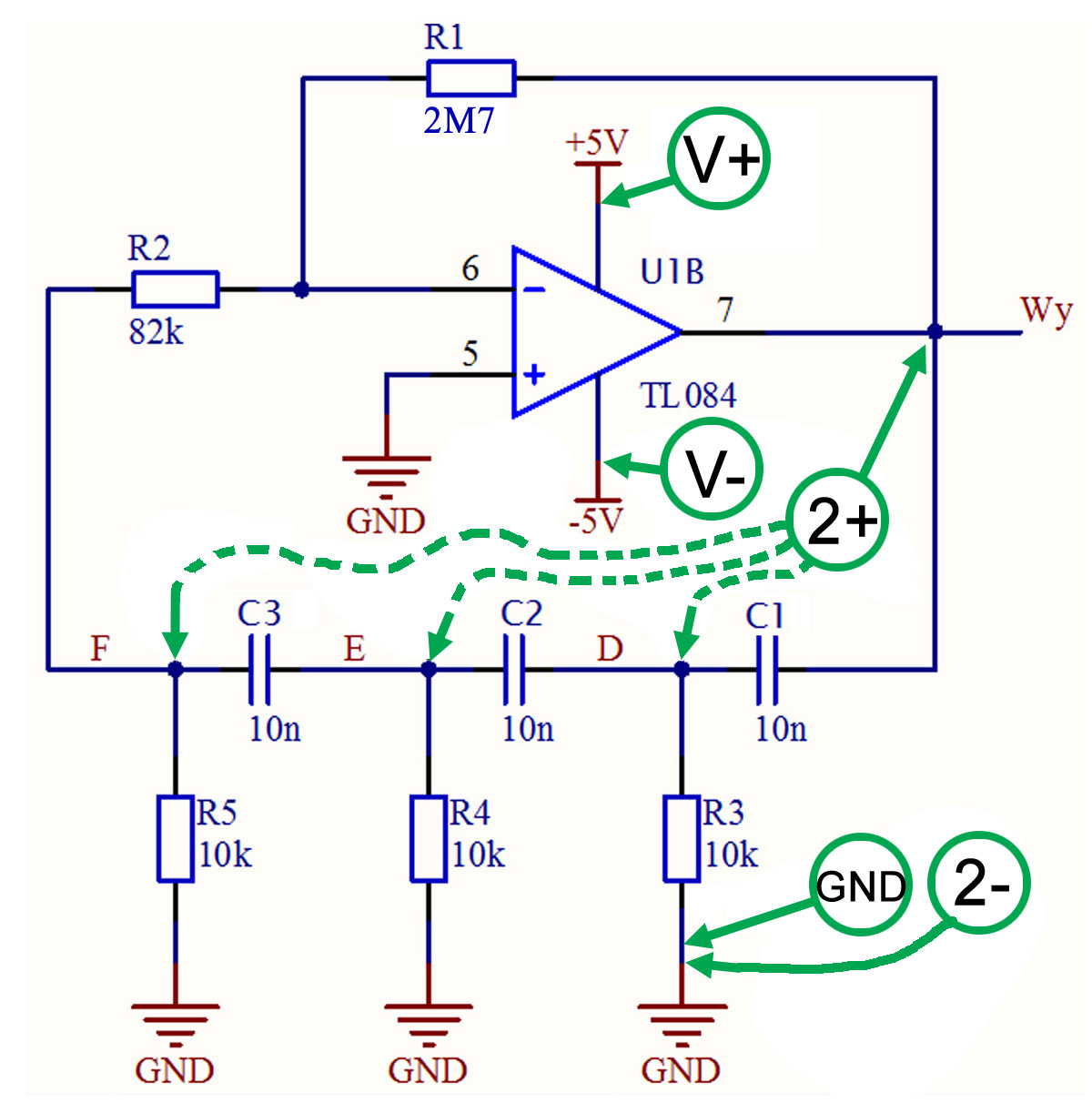
Rys. 8. Schemat pomiarowy generatora
Uaktywnij narzędzia Scope, Supplies i Spectrum programu WaveForms. Ustaw podstawę czasu na 500 μs/div, czułość kanału 2 = 735 mV/div, napięcia zasilające V+ = +5 V, V- = -5 V. Po wykonaniu wszystkich połączeń (rys. 9) uruchom narzędzia Supplies i Scope, a następnie obserwuj kolejno przebiegi w węzłach D, E i F zapamiętując je jako przebiegi referencyjne. Na koniec dołącz kanał 2 oscyloskopu do wyjścia generatora. Powinieneś obserwować przebiegi podobne do tych z rysunku 10.

Rys. 9. Połączenia elementów generatora
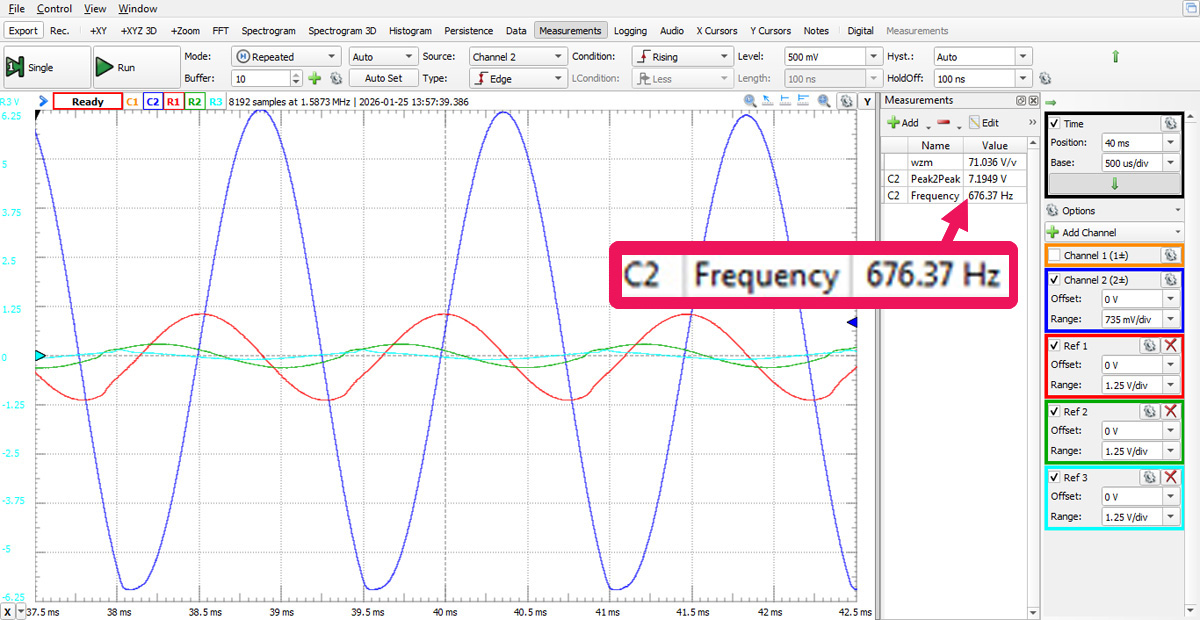
Rys. 10. Oscylogramy przebiegu wyjściowego generatora i przebiegów w poszczególnych węzłach przesuwnika fazy są bardzo zbliżone do tych z symulacji. W celu dokładniejszego ich porównania zmodyfikuj czułości kanałów referencyjnych tak, aby choćby w przybliżeniu wyrównać amplitudy poszczególnych przebiegów (rys. 11).
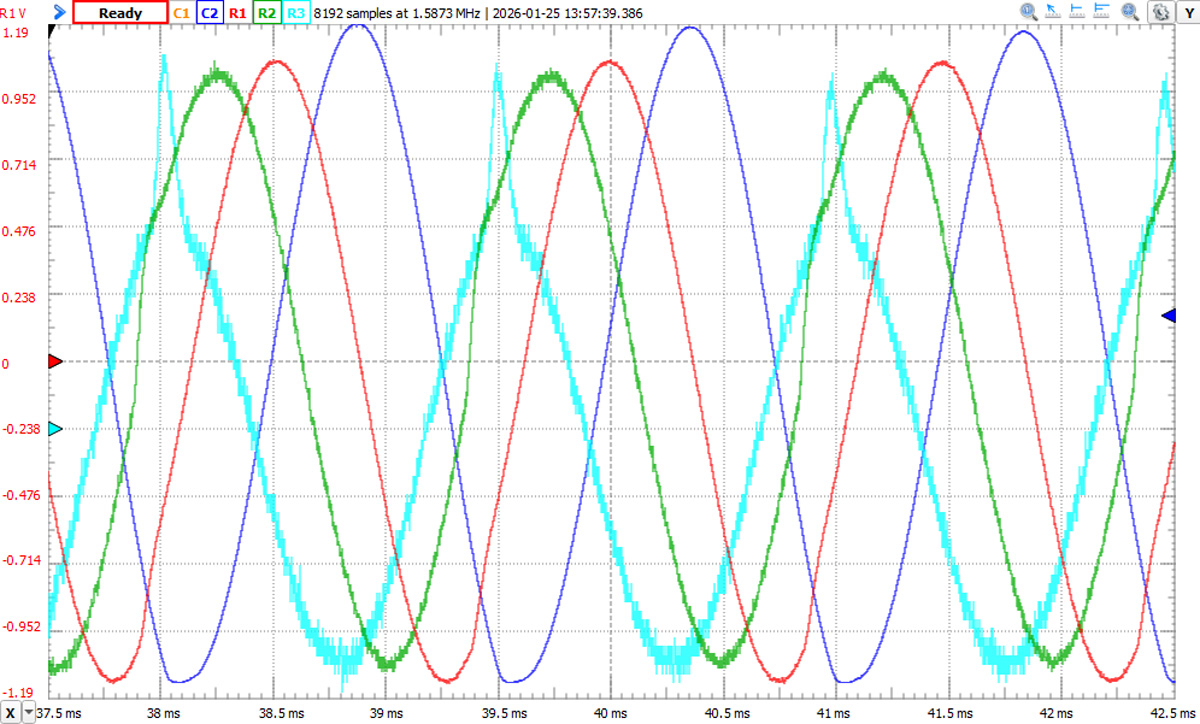
Rys. 11. Przebiegi napięciowe w różnych puntach generatora z wyrównanymi amplitudami do celów porównawczych
Teraz dokładnie można zaobserwować przesunięcia fazowe w poszczególnych węzłach przesuwnika oraz wyraźne zniekształcenia w jego ostatnim węźle (F), które obserwowaliśmy również w symulacji. Pozostaje jeszcze najważniejszy pomiar częstotliwości. W programie WaveForms obsługującym Analog Discovery 2 mamy do dyspozycji gotową funkcję mierzącą częstotliwość badanego sygnału. W tym przypadku odczytujemy, ze jest to 676,37 Hz wobec obliczonej teoretycznie 649,75 Hz.
Jednym z najważniejszych parametrów generatorów przebiegów sinusoidalnych są zniekształcenia dynamiczne. Obserwując oscylogram przebiegu wyjściowego można gołym okiem dopatrzyć się pewnych niedoskonałości przebiegu wyjściowego występujących z lewej strony dolnej połówki sygnału. Do ilościowego zmierzenia tych zniekształceń zastosujemy narzędzie Spectrum zestawu Analog Discovery 2. Ustawiamy zakres częstotliwości od 0 do 16 kHz, a z zestawu funkcji pomiarowych wybieramy THDp odpowiadający pomiarowi zniekształceń dynamicznych określających procentową zawartość harmonicznych w sygnale. W testowanym urządzeniu uzyskano wynik 2,535% (rys. 12).
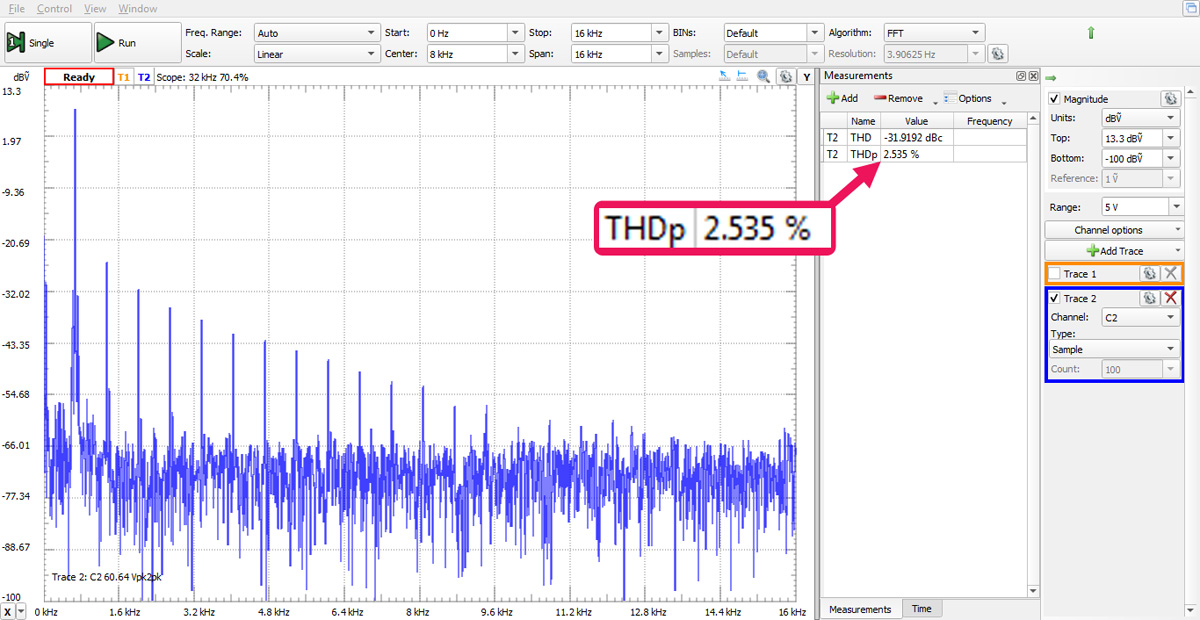
Rys. 12. Pomiar zniekształceń nieliniowych THD z zastosowaniem narzędzia Spectrum programu WaveForms
Hmmm… Rewelacji nie ma, ale też nie były wykonywane żadne zabiegi optymalizujące. Poza tym zastosowanie prostego, popularnego i taniego wzmacniacza operacyjnego TL084 również nie dawało gwarancji uzyskania wysokich parametrów.





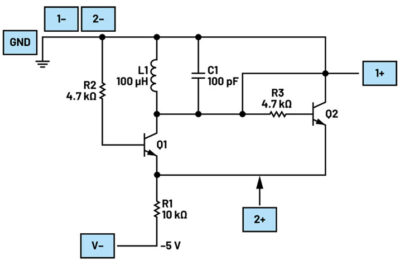 Generator Peltza – eksperyment z użyciem zestawu ADALM2000
Generator Peltza – eksperyment z użyciem zestawu ADALM2000 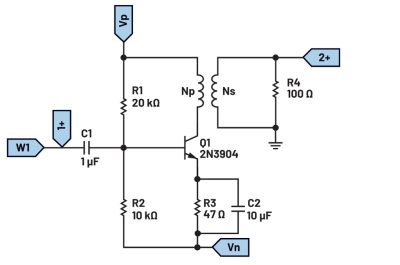 Zastosowanie zestawu ADALM2000 do pomiarów wzmacniacza sprzężonego transformatorowo
Zastosowanie zestawu ADALM2000 do pomiarów wzmacniacza sprzężonego transformatorowo 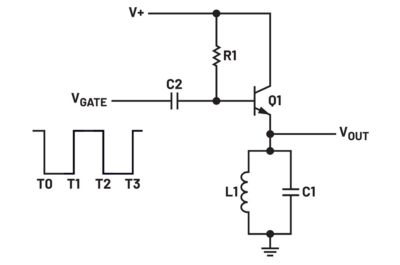 Generator impulsowy – pomiary wykonane z użyciem ADALM2000
Generator impulsowy – pomiary wykonane z użyciem ADALM2000 


![https://www.youtube.com/watch?v=kmvM5hVSzCM Piata już edycja konferencji Hardware Design Masterclasses dla elektroników zaskoczyła frekwencją, tym bardziej, że spotkanie było dwudniowe. Film jest krótką relacją z wydarzenia, bazującą na wypowiedziach prelegentów. [materiał redakcyjny] Zapraszamy do obejrzenia!](https://mikrokontroler.pl/wp-content/uploads/2026/01/Rafal-tytulowe.png)


