ZL31ARM: sterowanie kulki i obroty bryły w 3D za pomocą czujnika MEMS LIS35
Konfiguracja interfejsu SPI:
void SPI_Configuration(void){
SPI_InitTypeDef SPI_InitStructure;
GPIO_InitTypeDef GPIO_InitStructure;
// Enable SPI1 and GPIO clocks
RCC_APB2PeriphClockCmd(RCC_APB2Periph_SPI1 | RCC_APB2Periph_GPIOA, ENABLE);
// Configure SPI1 pins: SCK, MISO and MOSI
GPIO_InitStructure.GPIO_Pin = GPIO_Pin_5 | GPIO_Pin_6 | GPIO_Pin_7;
GPIO_InitStructure.GPIO_Mode = GPIO_Mode_AF_PP;
GPIO_InitStructure.GPIO_Speed = GPIO_Speed_50MHz;
GPIO_Init(GPIOA, &GPIO_InitStructure);
// Configure I/O for Flash Chip select
GPIO_InitStructure.GPIO_Pin = GPIO_Pin_CS;
GPIO_InitStructure.GPIO_Mode = GPIO_Mode_Out_PP;
GPIO_Init(GPIO_CS, &GPIO_InitStructure);
// SPI1 configuration
SPI_InitStructure.SPI_Direction = SPI_Direction_2Lines_FullDuplex;
SPI_InitStructure.SPI_Mode = SPI_Mode_Master;
SPI_InitStructure.SPI_DataSize = SPI_DataSize_8b;
SPI_InitStructure.SPI_CPOL = SPI_CPOL_High;
SPI_InitStructure.SPI_CPHA = SPI_CPHA_2Edge;
SPI_InitStructure.SPI_NSS = SPI_NSS_Soft;
SPI_InitStructure.SPI_BaudRatePrescaler = SPI_BaudRatePrescaler_256;
SPI_InitStructure.SPI_FirstBit = SPI_FirstBit_MSB;
SPI_InitStructure.SPI_CRCPolynomial = 7;
SPI_Init(SPI1, &SPI_InitStructure);
// Enable SPI1
SPI_Cmd(SPI1, ENABLE);
}
Kulka na wirtualnym stole
Mając do dyspozycji moduł wyświetlacza oraz akcelerometru jest możliwe zrealizowanie ciekawych programów sterujących. Pomysłów na to może być wiele, ale czasem zdarza się, że nie zawsze jest to takie proste w realizacji i niestety trzeba poznać pewne metody pozwalające osiągnąć zamierzone efekty. Na początku warto zacząć od prostych aplikacji jak np. sterowanie kulką na stole wirtualnym.
Fizyczna kulka posiada pewną masę, na którą działa siła przyciągania ziemskiego i które powoduje przyśpieszanie kulki, a zatem jej ruch. W naszym przypadku kulka co prawda nie posiada masy, ale można odczytać wartość przyśpieszenia z akcelerometru i za pomocą pewnych technik wprawić kulkę w ruch. Jak wiadomo z podstaw mechaniki klasycznej, położenie kulki na którą działa przyśpieszenie a jest określone następującym równaniem:
gdzie:
t – czas
s – pozycja bieżąca
s0 – pozycja początkowa
v – prędkość początkowa
a – przyśpieszenie
Dla potrzeb danego projektu powyższe równanie zostanie nieco zmodyfikowane w następujący sposób. Pozycja aktualna kulki będzie przechowywana w zmiennych x_pos i y_pos, które co pewien okres będą aktualizowane o wartości przemieszczenia delta_x i delta_y:
//Wyznaczanie aktualnej pozycji x_pos += delta_x; y_pos += delta_y;
Z kolei aktualne przemieszczenia są wynikiem iloczynu prędkości aktualnej i stałego okresu próbkowania Ts:
//Wyznaczanie aktualnego przemieszczenia delta_x = Vx*Ts; delta_y = Vy*Ts;
Ostatnie dwa równania określają aktualną prędkość kulki według wzoru:
//Wyznaczanie aktualnej prędkości; (x,y) – wartosci odczytanych przyspieszen Vx += (x/5)*Ts; Vy += (y/5)*Ts;
Wartości przyśpieszeń zostały podzielone przez 5 w celu poprawnej wizualizacji, tzn. aby kulka nie poruszała się za szybko. Jednocześnie można pójść dalej i wprowadzić tarcie wirtualne dla poruszającej się kulki co w pewnym stopniu nadaje cechy realistyczne:
//Uwzglednienie strat na skutek tarcia #define Tstrat 1 //Wspolczynnik strat if(Vx > 0) Vx -= Tstrat; //Stopniowe zmniejszanie prędkości else if(Vx < 0) Vx += Tstrat; //To samo ale z innym znakiem else Vx = 0; if(Vy > 0) Vy -= Tstrat; else if(Vy < 0) Vy += Tstrat; else Vy = 0;






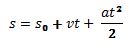
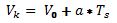
 Caroline Pannier – nowa dyrektorka targów electronica – analizuje sytuację gospodarczą branży i przedstawia wyniki
Caroline Pannier – nowa dyrektorka targów electronica – analizuje sytuację gospodarczą branży i przedstawia wyniki  Konstrukcja Ventiva Zoned Cooling™ – ukierunkowane chłodzenie powietrza dla urządzeń AI Edge
Konstrukcja Ventiva Zoned Cooling™ – ukierunkowane chłodzenie powietrza dla urządzeń AI Edge  Komunikacja dalekiego zasięgu oparta na technologii Qualcomm dla robotyki i dronów
Komunikacja dalekiego zasięgu oparta na technologii Qualcomm dla robotyki i dronów 






