Każdy przyrząd pomiarowy charakteryzuje się pewną klasą dokładności informującą użytkownika o maksymalnej wielkości błędu popełnianego podczas pomiarów. Klasa przyrządu jest gwarantowana przez producenta w chwili sprzedaży danego urządzenia, ale nie jest stała w czasie. Chcąc utrzymywać dokładność pomiarów w trakcie wieloletniej eksploatacji przyrządu użytkownik musi go okresowo kalibrować w wyspecjalizowanych laboratoriach.
Ideał nie istnieje
Metrologia to sztuka porównywania dwóch wielkości: mierzonej z wzorcową. Sztuka to nie łatwa, ponieważ żadna z tych wielkości nie jest na tyle jednoznacznie określona, żeby ze 100-procentową pewnością odnosić się do wyniku. Nie jest idealna wielkość mierzona, ale też zwykle daleka od ideału jest wielkość wzorcowa, referencyjna. Nie trudno zauważyć, że wynik pomiaru będzie tym bardziej zbliżony do wielkości rzeczywistej im lepsza będzie dokładność wzorca. Błąd popełniać będziemy jednak zawsze.
Mając świadomość tego, że zasadniczo żaden wynik pomiaru nigdy nie jest prawdziwy, warto zastanowić się, jak bardzo od niego się różni. Kwestia ta jest rozstrzygana zwykle przez wprowadzenie dwóch bliskoznacznych, ale nie tożsamych terminów. Są to: błąd i niepewność pomiaru. Niepewność charakteryzuje rozrzut wyników przyjmowanych jako prawidłowe. Można powiedzieć, ze niepewność jest wyrażana jako zakres tych wartości, które są uznawane za poprawne dla założonego poziomu ufności. Opierając się na tym parametrze, w zasadzie nigdy nie można wskazać jednego, unikatowego wyniku pomiaru, zawsze jest on traktowany jako pewien przedział. Mając to na uwadze, niepewność należy uznać za parametr lepiej charakteryzujący pomiar, niż powszechnie stosowane pojęcie błędu. Być może „popularność” błędu i bezpośrednio związanej z nim dokładności wynika z tego, że jest to pojęcie łatwiejsze do intuicyjnego zrozumienia, jednak w technice pomiarowej do oceny wyników pomiarów należy stosować niepewność. Mówiąc żartobliwie, może byłoby łatwiej, gdyby zamiast niepewności wprowadzono pojęcie pewności, ale tak oczywiście nie jest i raczej nie będzie. Dokładność natomiast na pewno nie zniknie z działań marketingowych, lepiej bowiem brzmi zdanie mówiące o wysokiej dokładności jakiegoś urządzenia niż o jego małej niepewności.
Trochę matematyki
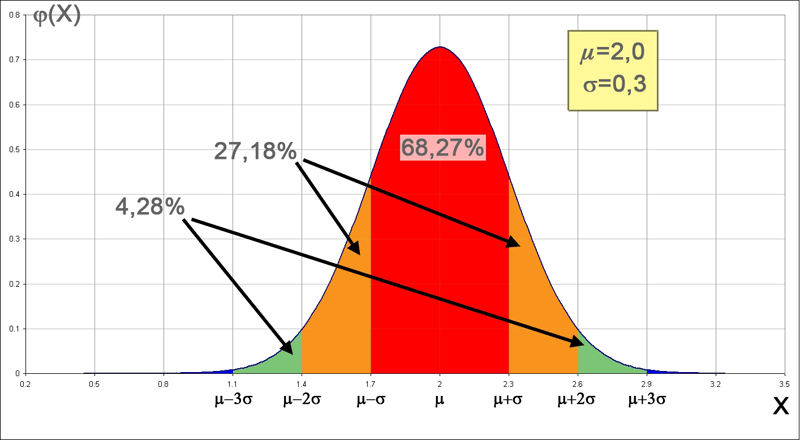
Wiemy już, że jednokrotny pomiar jakiejś wielkości da nam wynik, który prawdopodobnie odbiega od wartości rzeczywistej. Gdybyśmy teraz wykonali serię składającą się z dużej liczby takich pomiarów, z pewnością zauważylibyśmy, że jedne wartości będą powtarzały się częściej, inne rzadziej. Taki efekt jest dość dobrze widoczny w pomiarach cyfrowych, w których mamy tylko pewną określoną (dyskretną) liczbę wartości, np. na wyświetlaczu 4-cyfrowym liczba możliwych wskazań będzie równa 10000 (od 0 do 9999). Intuicyjnie można przypuszczać, że te wyniki, których liczba w całej serii pomiarów pojawiały się najczęściej, będą bardziej zbliżone do rzeczywistych niż te, które występowały rzadziej (przy założeniu, że przyrząd jest prawidłowo skalibrowany). Można teraz policzyć częstości występowania poszczególnych wartości w odniesieniu do całkowitej liczby pomiarów w serii. Wartości te z matematycznego punktu widzenia będą odpowiadały prawdopodobieństwom uzyskania poszczególnych wyników w serii pomiarów, a prawdopodobieństwo to będzie miało rozkład normalny (Gaussa). Wykres tego rozkładu przedstawiono na rysunku 1a. Jest to wykres teoretyczny, wyniki uzyskiwane w praktyce oczywiście odbiegają od niego. Na rysunku 1b przedstawiono rzeczywisty histogram pewnego zjawiska losowego, którego występowanie jest również charakteryzowane rozkładem Gaussa. Parametrem takiego rozkładu jest wartość oczekiwana μ i odchylenie standardowe σ. Na przykład dla rozkładu z rysunku 1a wartością oczekiwaną jest μ=2 a odchylenie standardowe jest równe σ=0,3. Na tej podstawie dochodzimy do wniosku, że rzeczywista wartość wielkości mierzonej jest wartością oczekiwaną rozkładu Gaussa o pewnym odchyleniu standardowym. Dla skończonej liczby wyników, z jaką będziemy mieli do czynienia w praktyce, wartość oczekiwana będzie się zbliżała do średniej ze wszystkich wyników. Kolejny wniosek wynikający z analizy krzywej rozkładu Gaussa dotyczy prawdopodobieństwa uzyskania wyniku różniącego się o określoną wartość od wartości oczekiwanej. I tak, dla różnicy nie większej niż odchylenie standardowe prawdopodobieństwo to jest równe 0,6827. Inaczej, oznacza to, że 68,27% pomiarów da wynik nie różniący się więcej niż odchylenie standardowe od wartości rzeczywistej. Do przedziału zawierającego się między –2σ+μ…μ+2σ trafi 95,45% wyników, a do przedziału –3σ+μ…μ+3σ trafi 99,73% wyników.
a)
b)
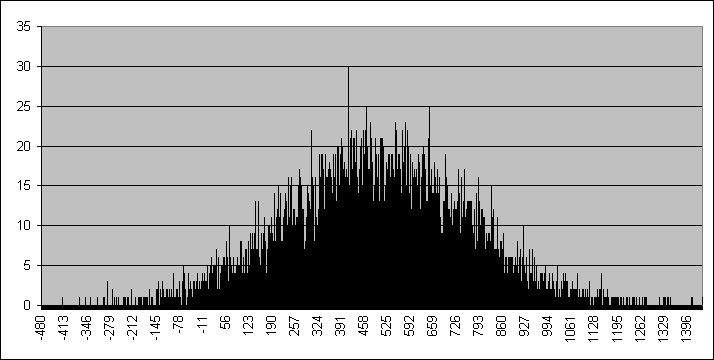
Rys. 1. Rozkład normalny (Gaussa) a) krzywa teoretyczna, b) praktyczne wyniki serii pomiarów
Rodzaje parametrów podawanych w katalogach
Informacje o dokładnościach poszczególnych parametrów danego urządzenia użytkownicy czerpią na ogół z katalogów, not katalogowych lub specyfikacji zamieszczanych w Internecie. Do prawidłowej ich interpretacji potrzebna jest znajomość kilku definicji:
- Parametry bez ograniczeń. W specyfikacjach nie są dla nich podawane żadne odchyłki. Przykładem takich parametrów są wymiary urządzenia, waga, rozdzielczość wskazań itp.
- Parametry typowe. Często podana wartość liczbowa jest uzupełniana o relację „<”, „>” lub podawany jest wprost zakres zmian, w którym powinno zmieścić się 80% wyrobów. W przeciwnym przypadku wartość typowa jest utożsamiana z wartością średnią.
- Parametry nominalne. Charakteryzują one własności produktu na podstawie reprezentatywnych dla niego wartości (np. impedancja). W odróżnieniu od parametrów typowych, statystyczny rozrzut parametrów nominalnych nie jest kontrolowany na etapie produkcji.
- Wartość zmierzona. Parametr uzyskany przez pojedynczy pomiar produktu.
- Niepewność pomiaru. Zauważmy, że powszechnie stosowana definicja błędu pomiaru mówiąca, że jest to różnica między wartością zmierzoną a wartością rzeczywistą jest z założenia bardzo nieścisła, wręcz błędna sama w sobie. Mierząc dany parametr nie jest bowiem znana wartość rzeczywista, a próbę jej ustalenia stanowi właśnie pomiar. Bardziej poprawnie ocenę wyniku pomiaru będzie więc charakteryzowała omówiona wcześniej niepewność pomiaru. Niepewność jest zapisywana jako odchyłka od wartości średniej uzyskanej w serii pomiarów: np.: U = 5,153 ± 0,012 V. Zasady obliczania i podawania niepewności są ujęte w dokumencie „Guide to the Expression of Uncertainty in Measurement” (GUM). Uwzględniono w nim nawet takie czynniki, jak warunki środowiskowe, starzenie elementów, ich zużywanie itp.
Porównania międzylaboratoryjne
Użytkownicy przyrządów pomiarowych powinni wykonywać okresowe badania aparatury, mające na celu potwierdzenie zadeklarowanych przez producenta parametrów, które ulegają zwykle zmianom w trakcie eksploatacji, w wyniku zużywania się materiałów, starzenia elementów itp. Badania takie są wykonywane w laboratoriach wchodzących w skład systemu oceny zgodności. Z kolei na laboratoriach tych spoczywa obowiązek weryfikacji swoich uprawnień w jednostkach wyższego poziomu. Jednym z elementów takich zadań weryfikacyjnych są porównania międzylaboratoryjne. Mówiąc w pewnym uproszczeniu, zadanie to polega na porównaniu pomiarów jednego urządzenia (ogólnie jakiegoś obiektu) wykonanych w różnych laboratoriach. Niestety, wiąże się to z kilkoma istotnymi aspektami technicznymi. Urządzenie referencyjne musi być transportowane kolejno do wszystkich laboratoriów biorących udział w porównaniach. Wynikająca z tego różnica czasu wykonywania pomiarów może nie być nie bez znaczenia. Zwykle należy też liczyć się ze zmianą warunków środowiskowych. Istotna jest więc dobra stabilność długoterminowa parametrów badanego urządzenia, ale też dokładność wytworzenia jednakowych warunków pomiarowych.
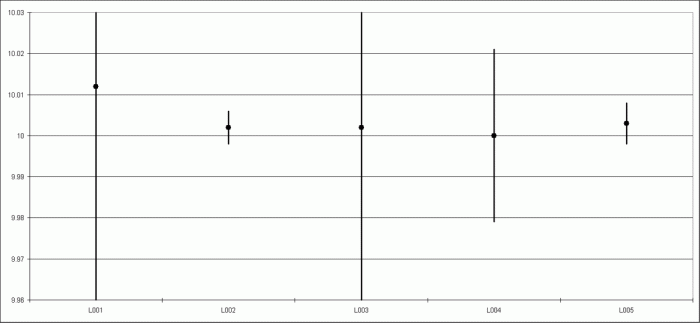
Jednym z najważniejszych parametrów przekazywanych organizatorowi badań przez każde laboratorium biorące udział w pomiarach jest całkowitą niepewność pomiarów. Między innymi na tej podstawie oceniane jest spełnienie warunków akredytacyjnych przez poszczególne jednostki. Na rysunku 2 przedstawiono wykresy niepewności pomiarowych uzyskanych przez 5 różnych laboratoriów biorących udział w porównaniu międzylaboratoryjnym. Mierzono moc na obciążeniu referencyjnym równą 100 W (100 V, 1 A) oraz 50 W (100 V 0,5 A). Jak widać z wykresu, w dwóch laboratoriach uzyskano niepewności pomiaru mocy 100 W mniejsze niż 0,010 W, pozostałych trzech niepewność ta była większa. Wszystkie laboratoria spełniły jednak stawiane im warunki. Na uwagę zasługuje laboratorium opisane symbolem L002, w którym pomiary były wykonywane precyzyjnym analizatorem mocy WT3000 produkowanym przez Yokogawę. W tabeli 1 przedstawiono wyniki serii pomiarów mocy wykonanych tym przyrządem wraz z podaniem niepewności pomiarowych. Analizator WT300 zapewnił uzyskanie wyników odznaczających się dużą stabilnością i małą niepewnością, co potwierdziło wysoką klasę tego przyrządu. Analiza mocy może być prowadzona tym przyrządem w zakresie częstotliwości aż do 100 kHz. Jest to ważne podczas badania zakłóceń generowanych przez zasilacze impulsowe, przetwornice napięciowe, nowoczesne systemy oświetleniowe, silniki elektryczne itp. Jednocześnie zakres częstotliwości analizatora WT3000 jest na tyle wysoki, że niewiele laboratoriów jest zdolnych do przeprowadzenia pełnej kalibracji tego przyrządu (w całym zakresie częstotliwości). Może być on natomiast z powodzeniem stosowany w laboratoriach certyfikujących. Opracowano dla niego szereg interfejsów umożliwiających pomiary mocy przy prądach do 1200 A, co dodatkowo rozszerza zakres zastosowań.
Tabela 1. Przykładowe wyniki serii pomiarów mocy wykonanych analizatorem mocy WR3000 Yokogawy
Częstotliwość
Napięcie
Prąd
Faza
Moc zmierzona
Niepewność
[Hz]
[V]
[A]
[°]
[W]
[W]
53
100
1
0
100,001
0,011
53
100
1
36,87
80,001
0,010
53
100
1
-36,87
80,001
0,011
53
100
1
60,00
50,000
0,010
53
100
1
-60,00
50,000
0,010
53
100
1
84,26
10,000
0,010
53
100
1
-84,26
10,000
0,010
53
100
1
0
500,193
0,033
53
100
1
36,87
400,125
0,033
53
100
1
-36,87
400,122
0,031
53
100
1
60,00
250,049
0,031
53
100
1
-60,00
250,047
0,030
53
100
1
84,26
50,002
0,030
53
100
1
-84,26
50,002
0,030
Rys. 2. Niepewność pomiarów mocy uzyskiwana w 5 laboratoriach biorących udział w porównaniach międzylaboratoryjnych
System zaufania
Laboratoria wykonujące usługowo kalibrację i certyfikację urządzeń pomiarowych powinny legitymować się odpowiednimi uprawnieniami wymaganymi do prowadzenia takiej działalności w systemie oceny zgodności. Stosowne uprawnienia są udzielane na drodze nadawania akredytacji danemu laboratorium, upoważniającej do prowadzenia określonej działalności. Instytucją udzielającą akredytacji jest Polskie Centrum Akredytacji (PCA). Akredytowane laboratoria dają gwarancję wykonywania usług na najwyższym poziomie. Klienci zlecający kalibrację przyrządów będą mieli pewność, że parametry badanych urządzeń będą zgodne ze specyfikacją techniczną, a na pewno nie gorsze. Usługę kalibracji warto więc zlecać tylko akredytowanym laboratoriom.
