Jak myśleć decybelami
Decybel (dB) jest jedna z najczęściej występujących jednostek w inżynierii. Jednocześnie sprawia on wiele trudności, zwłaszcza podczas przeliczania parametrów macierzy S. Oto kilka rad, które pomogą rozjaśnić to zagadnienie.
Bel to stosunkowo nowa jednostka, wprowadzona w roku 1928 przez Bell System w celu opisu natężenia dźwięku. Od tamtego czasu skala została uogólniona, aby wyrażać stosunek logarytmów dowolnych mocy. Najważniejsza zasada skali beli, którą należy rozumieć, jest fakt, ze wyraża ona stosunek mocy. Oryginalnie była to moc dźwięku, ale przyjęła się w opisie mocy dowolnego typu. Moc dźwięku zawiera się w bardzo szerokim zakresie. Próg słyszenia wynosi około 10–12 W/m2. Próg bólu wynosi 10 W/m2, a natężenie, które może zniszczyć bębenki to 1000 W/m2.
Najgłośniejszy zarejestrowany dźwięk wytworzony przez człowieka to start rakiety. Silniki Saturn V wywołały natężenie 100 W/m2 w odległości mili od miejsca startu. Wraz ze zbliżaniem się do tego miejsca, natężenie może być tylko wyższe.
Moc fali dźwiękowej odbitej od płyty lądowiska mogłaby z łatwością uszkodzić prom kosmiczny. Z tego powodu został zainstalowany system tłumienia zużywający 3,5 miliona litrów wody. Nawet z tym systemem natężenie dźwięku przy orbiterze wynosiło około 100 W/m2.
Różnica między progiem słyszenia a zniszczeniem bębenków to 15 rzędów wielkości. Operując w takim zakresie dynamicznym wygodnie jest używać wartości opisujących logarytm stosunku wielkości do poziomu odniesienia. W przypadku dźwięku poziomem odniesienia jest próg słyszenia. Szept ma moc około 100 razy większą, niż ten próg. Oznacza to wartość w belach
![]()
Odkurzacz ma moc około 10 milionów razy wyższą niż próg słyszenia. Daje to wartość 7 beli:
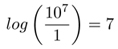
Na skali belowej głośność promu kosmicznego wynosi jedynie 14 beli. Pomimo ogromnej mocy nie wydaje się, aby 14 stanowiło duża liczbę. Aby ułatwić stosowanie w praktyce, skala została zwiększona 10 razy i używa jednostek równych 1/10 bela, czyli decybeli (dB).
Na przestrzeni ostatnich 85 lat skala dB została zaadoptowana do określenia innych rodzajów mocy, niż tylko moc dźwięku. Przyjmując poziom odniesienia równy 1 W, możemy określić wielkość innej mocy w decybelach. Jeśli przyjmiemy, ze poziom odniesienia jest równy 1 mW, wówczas stosowane są jednostki dBm – określają jednoznacznie, ze wyrażają wielkość w stosunku do mocy 1 mW.
Jest tu jednak pewna subtelność. Gdy chcemy porównać dwie wielkości, które nie są mocami, musimy w jakiś sposób przekształcić je w moc, do której da się zastosować skalę decybelową.
Napięcie nie określa mocy lecz amplitudę. Aby przejść na skalę decybelową w opisie napięcia, musimy przeliczyć napięcie na moc, a następnie wyznaczyć stosunek mocy odpowiadający tym napięciom.
Przykładowo, moc wydzielana w oporniku jest równa U*I lub U*I2/R. Możemy zatem wyznaczyć stosunek mocy wydzielonej na takim oporniku przez różne napięcia:
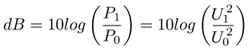
Rezystancja oczywiście się skraca. Możemy wyciągnąć kwadrat przed nawias i otrzymać następujący wzór:
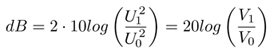
Teraz widać, skąd bierze się czynnik 20. Gdy chcemy wyrazić stosunek wielkości, które nie są mocami, lecz amplitudami, czynnik 20 pozwala zachować oryginalny stosunek. Ta wartość w decybelach oznacza naprawdę stosunek dwóch mocy wartości, które porównujemy. Czynnik 20 pozwala uzyskać stosunek logarytmów dwóch napięć.
Parametry macierzy S zawsze opisują stosunek dwóch napięć. Wobec tego do opisu macierzy S jest używany czynnik 20 i logarytm stosunku napięcia wyjściowego danych wrót do napięcia wejściowego. Zależność mocy od napięcia jest kwadratowa, zatem parametr S wyrażony w decybelach jest opisany wzorem:
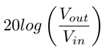
Następnie przyjrzymy się bliżej właściwościom skali decybeli, na przykład: jaki poziom napięcia odpowiada 10 dBm i czy impedancje w decybelach poprzedza się liczba 10 czy 20. Wiemy już, ze skala decybelowa (dB) opisuje stosunek dwóch mocy wzorem:
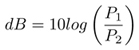
W przypadku mocy wzór jest poprzedzony wartością 10, a w przypadku napięcia – wartością 20. Parametry S, opisujące stosunek napięcia, używają wzoru z czynnikiem 20 w skali decybelowej. S11 równe -20 dB oznacza, ze odbity sygnał ma wartość:
![]()
Czyli 10% napięcia sygnału docierającego do wrót. Ponieważ moc zależy od kwadratu S11, moc odbita jest równa 1% mocy padającej:
![]()
Jest to dość dobry wynik dla większości elementów łączących sygnały cyfrowe.
Moc wyjściowa na poziomie –3 dB oznacza, ze jej stosunek do mocy wejściowej wynosi:
![]()
Jest to podstawowa zależność, której uczy się każdy inżynier – spadek o 3 dB oznacza zmniejszenie mocy o połowę. A co dzieje się z poziomem napięcia? Wartość -3 dB zawsze oznacza spadek mocy o 50%, ale napięcie wyjściowe w stosunku do napięcia wejściowego wynosi:
![]()
Gdy S21 jest równe –3 dB, poziom napięcia wyjściowego jest równy 70% napięcia wejściowego. Stosunek sygnału do szumu (SNR) jest zazwyczaj mierzony w decybelach. Zawsze i bez wyjątku oznacza on stosunek mocy sygnału do mocy szumu. SNR wyrażony w decybelach można łatwo przeliczyć na stosunek mocy w skali liniowej jako:
![]()
SNR równe 20 dB oznacza, ze moc sygnału jest stukrotnie wyższa, niż moc szumu. Jaki jest stosunek napięcia sygnału do napięcia szumu? Wynosi:
![]()
Wartość SNR równa 20 dB oznacza, ze sygnał ma moc 100 razy większą, niż szum, a napięcie 10 razy większe od napięcia szumu. Decybele są często stosowane do opisu przesłuchów. Poziom izolacji szumu -60 dB oznacza, ze moc szumu jest milion razy mniejsza niż moc sygnału:
![]()
Jednak napięcie szumu jest tylko 1000 razy mniejsze, niż napięcie sygnału:
![]()
W niektórych systemach sygnałów mieszanych wymagana jest izolacja -100 dB między odbiornikiem radiowym a szumiącymi układami cyfrowymi. Oznacza to, ze poziom napięcia odbieranych szumów ma wynosić 0,001% poziomu napięcia sygnału. Jest to bardzo małe sprzężenie, trudno je uzyskać w praktyce. W niektórych zastosowaniach impedancja jest mierzona w decybelach. Poziom odniesienia impedancji zawsze wynosi 1 Ω. Czy przy zamianie impedancji w omach na impedancję w dBΩ używamy współczynnika 10x czy 20x? Czy omy wyrażają amplitudę, czy moc?
Aby odpowiedzieć na to pytanie, należy zastanowić się, w jaki sposób impedancję można wyprowadzić z parametrów S. W przypadku pomiaru jednowrotnika, impedancja jest opisana wzorem:
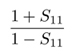
W przypadku dwuwrotnika impedancja wynosi około 25 Ω x S21. Impedancja jest związana z amplitudą, a zatem używa czynnika 20 podczas zamiany omów na decybele. Impedancja 0 dB w omach wynosi:
![]()
Jeśli impedancja jest równa 10 mΩ, w decybelach oznacza to wartość:
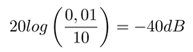
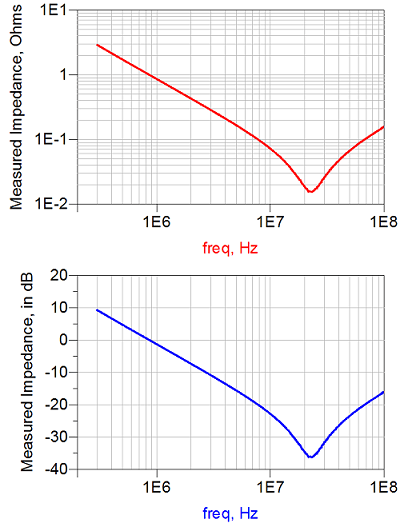
Rys. 1. Wartość impedancji kondensatora odsprzęgającego w skali liniowej i decybelowej
Na rysunku 1 pokazano impedancję kondensatora odsprzęgającego w skali liniowej i decybelowej. Górna część wykresy przedstawia impedancję w omach, dolna – impedancję w skali decybelowej.
Eric Bogan, Teledyne LeCroy







 Czy potężny rozbłysk słoneczny zagraża Ziemi? [opinia eksperta IŁ]
Czy potężny rozbłysk słoneczny zagraża Ziemi? [opinia eksperta IŁ]  Świetlana przyszłość przemysłu elektronicznego według Dave Doherty, prezesa zarządu DigiKey
Świetlana przyszłość przemysłu elektronicznego według Dave Doherty, prezesa zarządu DigiKey 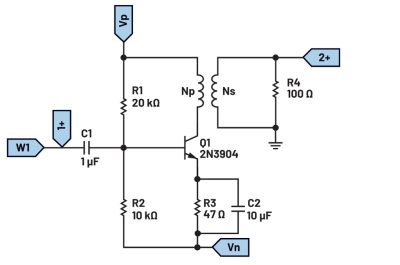 Zastosowanie zestawu ADALM2000 do pomiarów wzmacniacza sprzężonego transformatorowo
Zastosowanie zestawu ADALM2000 do pomiarów wzmacniacza sprzężonego transformatorowo