1. Wstęp

Wprowadzenie oscyloskopów wysokiej rozdzielczości stanowi odpowiedź na rosnące potrzeby bardziej zaawansowanej analizy sygnałów w takich zastosowaniach, jak lotnictwo i astronautyka, motoryzacja, medycyna i analiza zużycia mocy. W tych obszarach zachodzi konieczność obserwacji zarówno sygnałów o wysokiej, jak i niskiej amplitudzie napięcia. Charakteryzacja zasilaczy impulsowych stanowi jeden z przykładów zastosowań. Aby zapewnić dokładny pomiar mocy, oscyloskopy muszą rejestrować napięcie w stanie włączenia i wyłączenia na tym samym przebiegu. Wymaga to większego zakresu dynamicznego, niż może zapewnić 8 bitów, ponieważ skoki napięcia mogą wynieść wiele setek woltów. Innym przykładem jest analiza sygnałów radiowych z modulacją amplitudy o niewielkiej głębokości modulacji, często spotykanych w radarach.

Przydatność oscyloskopów w takich zastosowaniach zależy w głównej mierze od rozdzielczości pionowej. Stanowi ona coraz bardziej istotny czynnik, obok standardowych parametrów, takich jak pasmo, częstotliwość próbkowania i rozmiar pamięci. Rozdzielczość pozioma decyduje o precyzji wyświetlenia szczegółów na ekranie oscyloskopu i określa, z jaką dokładnością można te szczegóły mierzyć i analizować.

Kluczowym elementem oscyloskopu cyfrowego związanym z rozdzielczością pionową jest przetwornik analogowo-cyfrowy. Zamienia on sygnał analogowy z kanału wejściowego oscyloskopu na próbki dyskretnego czasu i wartości, które mogą zostać przetworzone i zapisane w pamięci przyrządu. Rozdzielczość czasowa przebiegu próbek odpowiada częstotliwości próbkowania przetwornika. Z kolei liczba bitów przetwornika określa rozdzielczość pionową.

W oscyloskopach cyfrowych typowo stosowane są przetworniki 8-bitowe. Niektóre wyspecjalizowane modele oferują większą rozdzielczość pionową, niż 8 bitów. Jednym z możliwych sposobów jej zwiększenia jest użycie przetwornika o liczbie bitów większej, niż 8. Innym sposobem zwiększenia rozdzielczości jest zastosowanie technik przetwarzania sygnałów w ścieżce akwizycji.

W obu przypadkach należy pamiętać, że liczba bitów określająca przetwornik analogowo-cyfrowy jest tylko teoretyczna. Prawdziwa rozdzielczość, określana jako „efektywna liczba bitów” (ENOB), jest niższa od wartości nominalnej za sprawą takich efektów, jak szumy, nieliniowość oraz zniekształcenia. Co więcej podczas określania parametrów dynamicznych oscyloskopu trzeba uwzględnić parametry innych układów wejściowych, takich jak wzmacniacz, filtr i elementy pasożytnicze.

W niniejszym artykule zostały opisane rozszerzenia wysokiej rozdzielczości R&S RTO-K17 oraz R&S RTE-K17, odpowiednio dla oscyloskopów cyfrowych R&S RTO oraz R&S RTE. Rozszerzenia zwiększają rozdzielczość pionową i czułość układu wyzwalania oscyloskopów z obu rodzin do 16 bitów, stosując cyfrową filtrację sygnału na ścieżce akwizycji. Rozszerzenie można łatwo aktywować w dowolnym momencie przez wprowadzenie klucza.

W rozdziale 2. została wyjaśniona warstwa teoretyczna oraz zastosowana technika filtracji. Rozdział 3. zawiera porównanie metod przetwarzania, które zwiększają rozdzielczość i pokazuje zalety rozszerzenia wysokiej rozdzielczości R&S. W rozdziale 4. znajdują się opisy przykładowych pomiarów. [Rozdziały te zostaną opublikowane w następnej kolejności – przyp. redakcji]

W artykule są używane następujące skróty:

• RTO – cyfrowy oscyloskop R&S RTO, RTE – cyfrowy oscyloskop R&S RTE
• Tryb HD – rozszerzenie wysokiej rozdzielczości R&S RTO-K17 / R&S RTE-K17

2.   Opis teoretyczny

Większa rozdzielczość nie przekłada się automatycznie na większą dokładność. Przed bliższym zapoznaniem z trybem HD warto wymienić typowe terminy opisujące system pomiarowy.

Standard ISO (1) definiuje większość z tych terminów, jednak w tej nocie zostały one użyte w nieco innym znaczeniu typowym dla oscyloskopów. Jest tak, ponieważ standard nie uwzględnia cyfrowej postaci wyników pomiarów. Jednak konwersja do postaci cyfrowej nie może zostać pominięta przy analizie trybu HD. Z tego powodu wykorzystano słowo „rozdzielczość” tam, gdzie standard używa terminu „precyzja”. Słowo „precyzja” oznacza wartość liczbową i jest wspólne dla informatyki oraz cyfrowego przetwarzania sygnałów. Terminy „dokładność” i „obciążenie” mają takie same znaczenia, jak w standardzie ISO.

2.1  Definicje terminów

• Dokładność – opisuje odchylenie wyników kolejnych pomiarów od prawdziwej wartości. Zależy od rozdzielczości, precyzji i obciążenia.
• Obciążenie – efekty nie-losowe, które powodują różnicę między wartością średnią pomiarów a prawdziwą wartością.
• Rozdzielczość – losowe rozproszenie mierzonych wartości wokół średniego wyniku pomiarów to rozdzielczość. Średnia pomiarów nie musi być tożsama z prawdziwą wartością i może być obciążona. Z tego powodu wysoka precyzja nie musi przekładać się na wysoką dokładność.
• Precyzja – wartość minimalnej różnicy między dwiema wartościami numerycznymi wyrażającymi wynik.

Rysunek 2.1. przedstawia dokładność, precyzję i rozdzielczość. Widać na nim cztery cele i chmurę dziewięciu punktów, rozproszonych i obciążonych. Ten rysunek jest znany, natomiast może występować pewna różnica w znaczeniu koncentrycznych okręgów.

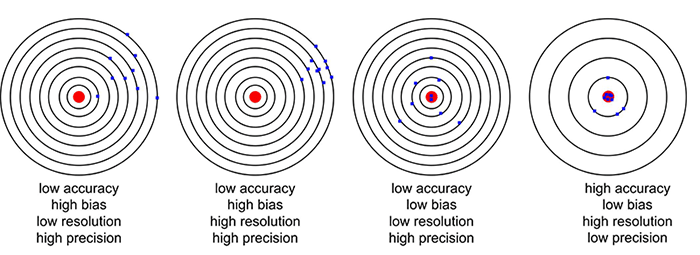
Rysunek 2.1. Porównanie dokładności, obciążenia, rozdzielczości i precyzji 

Koncentryczne okręgi symbolizują precyzję – im więcej okręgów, tym wyższa precyzja i tym więcej szczegółów może opisać wynik pomiaru. Każdy pomiar, oznaczony niebieską kropką, musi znajdować się na okręgu. Czerwony punkt w środku oznacza prawdziwą wartość. Pierwsze trzy rysunki od lewej przedstawiają wysoką precyzję, prawy – niższą precyzję.

Pierwszy rysunek od lewej ma niską rozdzielczość, wysokie obciążenie i niską dokładność. Drugi obrazek ma wysoką rozdzielczość, ale z powodu obciążenia dokładność jest niska. Kolejny obrazek ma wysoką dokładność, ale niską rozdzielczość. Ostatni przedstawia wysoka dokładność i wysoką rozdzielczość, choć jego precyzja jest niższa. Ta ilustracja jasno pokazuje, że pomiar dokonany z wyższą precyzją nie musi być jednoznacznie bardziej dokładny, niż pomiar z niższą precyzją. Przeciwnie – pokazuje, że pomiar z niższą precyzją może być bardziej dokładny.

Od przyrządów takich, jak oscyloskopy, użytkownicy oczekują wysokiej dokładności dla dowolnego sygnału. Jednak nota katalogowa z reguły opisuje tylko dokładność pomiaru DC, a nie dokładność pomiaru AC. Zamiast tego często znajduje się informacja o precyzji lub nominalnej rozdzielczości pionowej przetwornika analogowo-cyfrowego. Rysunek 2.1 pokazuje, że nie można wywnioskować dokładności jedynie na podstawie nominalnej precyzji.

W oscyloskopie nominalna precyzja wynika z architektury sprzętowej. Błędy systematyczne wnoszone przez realizację sprzętową, takie jak szumy i nieliniowość w stanie dynamicznym, determinują rozdzielczość. Natomiast losowe błędy występujące w systemie – niezrównoważenie i nieliniowość statyczna – powodują występowanie obciążenia. Na te zjawiska mają wpływ różne podukłady, nie tylko przetwornik.

Typowe przetworniki AC stosowane w oscyloskopach mają precyzję 8 bitów. Niektóre wyspecjalizowane przyrządy mają przetworniki o nominalnej rozdzielczości lub precyzji 10-12 bitów. Jeśli oscyloskop ma dobrą dokładność i rozdzielczość, wówczas i tylko wówczas wzrost precyzji przełoży się na wzrost rozdzielczości i wówczas zwiększy rozdzielczość, a tym samym dokładność pomiaru – drobniejszy odstęp między wartościami w osi pionowej.

Kolejne części opisują w jaki sposób cyfrowe przetwarzanie sygnałów pozwala zwiększyć rozdzielczość i precyzję.

2.2  Stosunek sygnału do szumu a efektywna liczba bitów (ENOB)

Karta katalogowa oscyloskopu nie określa dokładności i rozdzielczości dla sygnałów zmiennych. Różnego typu błędy przetwornika analogowo-cyfrowego ograniczają dokładność oscyloskopu. Z tego powodu ważne jest zrozumienie, w jaki sposób rozdzielczość oscyloskopu jest związana z precyzją wyrażoną w liczbie bitów.

Nominalna precyzja przetwornika nie jest równa efektywnej rozdzielczości oscyloskopu. Efektywną rozdzielczość oscyloskopu można określić, mierząc stosunek sygnału do szumu (SNR). (2). Na podstawie SNR można wyznaczyć ENOB, który mierzy efektywna rozdzielczość.

W przypadku idealnego przetwornika zależność między obliczonym SNR a rozdzielczością została opisana w pozycji (3) i jest wyrażona wzorem 2.1:

Wzór 2.1