Oscyloskop z rzeczywistym przetwornikiem analogowo-cyfrowym zachowuje się gorzej z powodu szumu, nieliniowości i zniekształceń. Aby powiązać prawdziwy przetwornik z jego idealnym modelem, przyjmuje się średniokwadratową wartość błędu kwantyzacji równą średniokwadratowej wartości szumu (i zniekształceń) oscyloskopu. Na podstawie zmierzonej wartości SNR można obliczyć efektywną rozdzielczość (liczbę bitów). Wzór 2.2 przedstawia tą zależność. Rozdzielczość jest wyrażona w bitach idealnego przetwornika analogowo-cyfrowego i nie musi być liczbą całkowitą. Właśnie ta rozdzielczość jest nazywana efektywną liczbą bitów (ENOB).

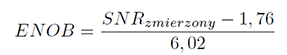
Wzór 2.2

W oscyloskopach z rzeczywistymi przetwornikami wartość ENOB będzie mniejsza od precyzji wyrażonej w bitach na skutek szumów i zniekształceń. Oscyloskopy RTO i RTE cechują się niskimi szumami w układach wejściowych. Wykorzystany przetwornik analogowo-cyfrowy ma nominalną rozdzielczość 8 bitów i ENOB powyżej 7 bitów do częstotliwości 4 GHz.

2.3  Redukcja szumów i filtracja

W poprzedniej części zostały omówione zależności między precyzją, obciążeniem, rozdzielczością i stosunkiem sygnału do szumu. W tej części jest opisany wpływ filtru na widmo sygnału i szumu oraz wynikający z tego zysk rozdzielczości. Te rozważania pomijają wpływ zniekształceń, co jest racjonalnym założeniem przy wysokiej liniowości analogowych układów wejściowych przyrządów RTO oraz RTE.

Tendencje w rozwoju przetworników analogowo-cyfrowych (4) pokazują, że częstotliwość próbkowania kolejnych modeli znacznie wzrasta na przestrzeni lat, natomiast ich rozdzielczość pozostaje względnie stała. Mając to na uwadze, zostały opracowane techniki zwiększające rozdzielczość przetwornika analogowo-cyfrowego w domenie cyfrowej. Jedna z nich jest przedstawiona w tej części. Techniki te wymieniają częstotliwość próbkowania na rozdzielczość pionową dzięki nadpróbkowaniu. Typowym przykładem jest 1-bitowy przetwornik sigma-delta używany z sygnałami audio o rozdzielczości 24 bitów.

Szum idealnego przetwornika A/C, jak również szum równoważnego rzeczywistego przetwornika A/C można opisać jako szum biały (3). Szum biały ma równomierne widmo mocy, co oznacza że w przedzialewidmowa gęstość mocy p_N(f) jest stała. Wartość widmowej gęstości mocy szumu jest wówczas równa całkowitej średniokwadratowej mocy szumów p_N dzielonej przez częstotliwość próbkowania f_a.

W przypadku nadpróbkowania pasmo sygnału  jest znacznie mniejsze od częstotliwości próbkowania f_a. Można wówczas ograniczyć pasmo bez zmiany tego sygnału . W celu uproszczenia opisu w tej części przyjęto filtr o charakterystyce prostokątnej  i częstotliwości odcięcia f_B. Sytuacja ta została przedstawiona na rysunku 2.2. Z rysunku można wywnioskować, że całkowita moc szumu została zmniejszona o stosunek częstotliwości próbkowania do częstotliwości odcięcia. Zysk w decybelach opisuje wzór 2.4.

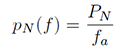
Wzór 2.3

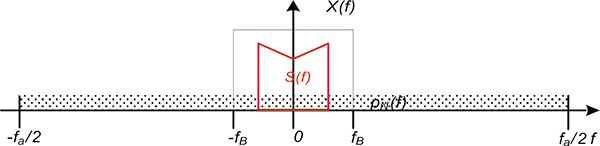
Rysunek 2.2. Obniżenie mocy szumów dzięki filtracji

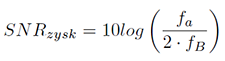
Wzór 2.4

Proakis (3) dowiódł, że podwojenie częstotliwości próbkowania f_a przy zachowaniu pasma filtru zmniejsza moc szumów i tym samym poprawia SNR razy, lub 3 dB co przekłada się na 1/2 bitu. Gdy częstotliwość próbkowania zostanie zwiększona czterokrotnie, lub o 6 dB, zysk rozdzielczości wynosi 1 bit, co wynika ze wzoru 2.2.

2.4  Filtr redukujący szumy

W poprzednich częściach została opisana zależność dokładności i rozdzielczości, a także sposób poprawny rozdzielczości za pomocą filtru dolnoprzepustowego. W ten części zostanie pokazane, w jaki sposób filtr ogranicza pasmo i zwiększa precyzję, dzięki czemu zysk rozdzielczości przełoży się na wyższą precyzję.

Dostępnych jest kilka rodzajów filtrów dolnoprzepustowych ograniczających pasmo. W tej części został wybrany filtr uśredniający (moving average, MAV) w celu uproszczenia opisu. Filtr MAV oblicza wartość każdej próbki wyjściowej na podstawie M ostatnich próbek . W tym kontekście parametr M oznacza długość filtru. W przypadku średniej arytmetycznej, matematyczna definicja wymaga podziału przez długość filtru M, co zapewnia, że średnia moc na wyjściu filtru jest taka sama, jak moc sygnału wejściowego. Wzór 2.5 przedstawia dokładną definicję. W dalszych rozważaniach przyjęto długość filtru równą 2 i ciąg wejściowy  zawierający liczby całkowite ze znakiem o długości 8 bitów.

Tak opisany filtr MAV sumuje dwie ostatnie próbki i dzieli wynik przez 2, tzn. . Uzyskana suma dla próbek 8-bitowych zawiera się w przedziale od -256 do 254, ponieważ próbki wejściowe przyjmują wartości od -128 do 127. W przypadku arytmetyki stałoprzecinkowej na przechowanie wyniku potrzebne jest 9 bitów, aby przedstawić 511 możliwych wartości wyjściowych. Efektem tej operacji jest zysk 1 dodatkowego bitu w stosunku do wejściowych wartości 8-bitowych. W przypadku arytmetyki stałoprzecinkowej ten zysk można zachować również po operacji dzielenia, w tym przypadku przez 2.

Powyższy przykład można uogólnić dla dowolnej długości filtra M, który wykorzystuje arytmetykę stałoprzecinkową, gdzie M jest dodatnią liczbą całkowitą. Dla dowolnego M zysk precyzji jest równy logarytmowi o podstawie 2 z długości filtra MAV. W przypadku, gdy długość filtra stanowi potęgę 2 (2, 4, 8, 16…) zysk jest liczbą całkowitą (1, 2, 3, 4…). Dla innych długości filtra zysk precyzji jest wartością ułamkową, a arytmetyka stałoprzecinkowa powoduje obcięcie wyniku do precyzji wynikającej z implementacji sprzętowej. W przypadku oscyloskopów RTO i RTE precyzja sprzętowa wynosi 16 bitów. Błąd wnoszony przez obcinanie jest pomijalny.

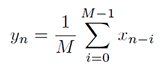
Wzór 2.5

Powodem stosowania długości filtrów innych, niż potęgi 2, stają się oczywiste po analizie powstałego w ten sposób pasma filtru. W części 2.3 została omówiona redukcja szumu w zależności od stosowanego pasma filtru. W tej części został już omówiony wzrost precyzji, natomiast teraz zostanie wyjaśniony związek między precyzją, pasmem filtru i rozdzielczością.

Odpowiedź impulsowa  filtru uśredniającego jest funkcją prostokątną dyskretną w czasie, co pokazano na rysunku 2.3. Transmitancja  w dziedzinie częstotliwości to dyskretna transformata Fouriera odpowiedzi impulsowej.

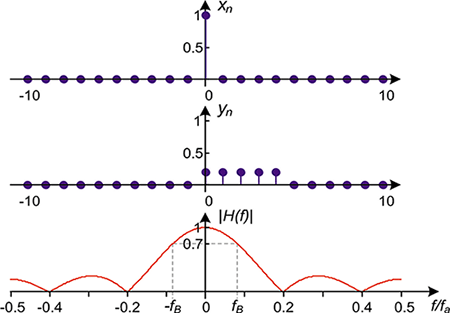
Rysunek 2.3. Odpowiedź impulsowa filtru i pasmo filtru uśredniającego o długości M = 5

Wzór 2-6 opisuje moduł transmitancji || w dziedzinie częstotliwości dla filtru uśredniającego. Proakis (3) przedstawia szczegółowe wyprowadzenie transmitancji. Częstotliwość  jest wyskalowana w częstotliwości próbkowania  i zawiera się w zakresie od -0,5 do 0,5 . Częstotliwość odcięcia  to taka wartość, dla której sygnał jest tłumiony o 3 dB – do wartości 0,7 względem pasma przepustowego. Częstotliwość  zależy od długości filtru M. Nie da się wyrazić jej wzorem jawnym.

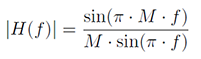
Wzór 2.6

Dla przykładowego filtru MAV o długości M = 5 szerokość pasma  wynosi . Zysk precyzji wynosi około 2,3 bitu, natomiast poprawa stosunku sygnału do szumu wynosi 7,4 dB zgodnie ze wzorem 2.4.

2.5  Ograniczenia metody redukcji szumów

Istnieją ograniczenia omówionej metody, które użytkownik powinien uwzględnić. Najbardziej znaczącym ograniczeniem zmniejszenia szumów są zniekształcenia spowodowane nieliniowością przetwornika A/C w układach wejściowych, które nie mogą zostać zmniejszone. Błędy te można testować za pomocą sygnału sinusoidalnego. Miarą zniekształceń jest zakres dynamiczny (SDFR) opisany w pozycji (5). Jest on wyrażony w dB i im jest większy, tym mniejsze są zniekształcenia. W poprzednich częściach zniekształcenia były pominięte poprzez założenie, że przetwornik A/C jest idealny, jednak w rzeczywistej sytuacji SFDR ograniczy zysk rozdzielczości dla wąskiego pasma filtru.

Standard IEEE (5) jest bardziej precyzyjny i rozróżnia wpływ szumów oraz zniekształceń. Wprowadza również współczynnik SINAD (stosunek sygnału do szumu i zniekształceń). Dla szerokiego pasma SINAD zależy głównie od szumów. Przy obniżaniu szumów poprzez filtrację to zniekształcenia zaczynają odgrywać główną rolę i mają dominujący wpływ na SINAD.

Wartość SFDR została zmierzona dla RTO z 8-bitowym przetwornikiem analogowo-cyfrowym o częstotliwości próbkowania 4 GHz za pomocą wyspecjalizowanego oscyloskopu o większej precyzji, niż 8 bitów. W pomiarów wynika, że minimalne wartości SFDR są porównywalne (wykres 2.4). Wysoką rozdzielczość oscyloskopu ogranicza SFDR, którego minimalna wartość wynosi 46 dB.

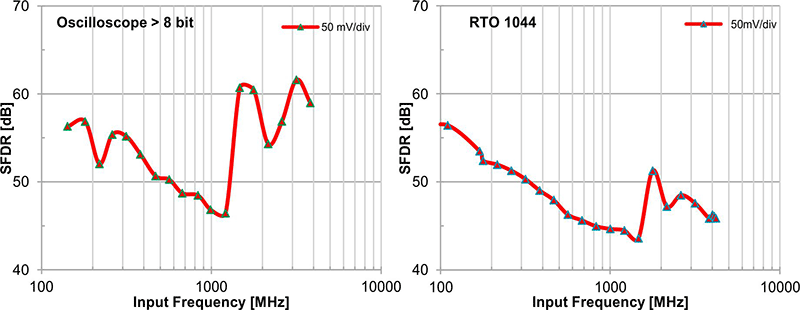
Wykres 2.4. Porównanie współczynnika SFDR dla oscyloskopu wysokiej rozdzielczości oraz modelu RTO1044

Kolejnym ograniczeniem jest szerokość linii danych przetwarzającej próbki. Sprzętowa precyzja musi być wystarczająca do reprezentacji zwiększonej rozdzielczości. Dla oscyloskopów RTO i RTE szerokość linii danych w rozszerzeniu HD wynosi 16 bitów, co jest unikalną cechą tych oscyloskopów.

Warto również pamiętać, że dotychczasowe rozważania oparte są na założeniu o równomiernym poziomie szumów. O ile to założenie jest wiarygodne, może nie być spełnione dla wysokiego stosunku częstotliwości próbkowania do częstotliwości odcięcia filtru cyfrowego. W takim przypadku wpływ szumu nie jest już pomijalny, a wzór 2.4 przestaje być prawdziwy. Ten efekt prowadzi do obniżenia zysku SNR.