Biblioteka DSP dla mikrokontrolerów LPC1700 i LPC1300 firmy NXP
Szybka transformata Fouriera
Dyskretna transformata Fouriera (DFT) jest powszechnie wykorzystywaną transformatą stosowaną w takich dziedzinach, jak telekomunikacja, przetwarzanie sygnałów audio – mowy i muzyki, a także w cyfrowym przetwarzaniu obrazów.
Istnieje wiele wydajnych algorytmów implementujących DFT, ale w praktyce okazuje się, że pewne algorytmy lepiej nadają się dla konkretnych architektur układów. Architektura ARM w ogólności, za sprawą banku rejestrów 16-bitowych, osiąga największą wydajność FFT za pomocą transformaty radix-4 .
Wzór DFT:
gdzie:
Prototypy funkcji DFT:
void vF_dspl_fftR4b16N64(short int *psi_Y, short int *psi_x);
void vF_dspl_fftR4b16N256(short int *psi_Y, short int *psi_x);
void vF_dspl_fftR4b16N1024(short int *psi_Y, short int *psi_x);
void vF_dspl_fftR4b16N4096(short int *psi_Y, short int *psi_x);
Wydajność FFT przedstawiono w tabeli 2.
Tab. 2. Wydajność FFT w zależności od jej rozmiaru
| FFT | Mnożnik zegara pamięci 1 | Mnożnik zegara pamięci 2 | Mnożnik zegara pamięci 3 | |||
| (20 MHz maks.) | (40 MHz maks.) | (60 MHz maks.) | ||||
| liczba współczynników | Cykle | Czas (ms) | Cykle | Czas (ms) | Cykle | Czas (ms) |
| 64 punktów | 3895 | 0,195 | 4035 | 0,101 | 4202 | 0,070 |
| 256 punktów | 21107 | 1,055 | 21719 | 0,543 | 22339 | 0,372 |
| 1024 punktów | 107007 | 5,350 | 110161 | 2,754 | 113326 | 1,889 |
| 4096 punktów | 518926 | 25,946 | 538209 | 13,455 | 557494 | 9,292 |
| FFT | Mnożnik zegara pamięci 4 | Mnożnik zegara pamięci 5 | Mnożnik zegara pamięci 6 | |||
| (80 MHz maks.) | (100 MHz maks.) | (120 MHz maks.) | ||||
| liczba współczynników | Cykle | Czas (ms) | Cykle | Czas (ms) | Cykle | Czas (ms) |
| 64 punktów | 4384 | 0,055 | 4816 | 0,046 | 4616 | 0,038 |
| 256 punktów | 22961 | 0,287 | 23884 | 0,239 | 23884 | 0,199 |
| 1024 punktów | 116749 | 1,459 | 121657 | 1,217 | 121657 | 1,014 |
| 4096 punktów | 578059 | 2,226 | 600694 | 6,007 | 600694 | 5,006 |
Iloczyn skalarny
W tej funkcji zaimplementowano iloczyn skalarny o 32-bitowej precyzji. W każdym obiegu pętli asemblera wykonywane jest jedno mnożenie, by zmaksymalizować swobodę w doborze długości wektora, ale pętlę można też rozwinąć dla ustalonych długości wektorów.
Wzór na iloczyn skalarny:
Prototyp funkcji iloczynu skalarnego:
int iF_dspl_dotproduct32(int *pi_x, int *pi_y, int i_VectorLen);
Szybkość obliczeń:
N = liczba cykli
N = (8*i_długość_wektora)+8
Założenie: wszystkie pobrania instrukcji trwają jeden cykl.
Dodawanie wektorów
Prototyp funkcji VectAdd16:
void vF_dspl_vectadd16(int *psi_z, int *psi_x, int *psi_y, int i_VectorLen);
Prototyp funkcji VectAdd32:
void vF_dspl_vectadd32(int *pi_z, int *pi_x, int *pi_y, int i_VectorLen);
Wydajność obliczeń przedstawiono w tabeli 3.
Tab. 3. Dodawanie wektorów
| Mnożnik zegara pamięci 1 | Mnożnik zegara pamięci 2 | Mnożnik zegara pamięci 3 | ||||
| Dodawanie wektorów | (20 MHz maks.) | (40 MHz maks.) | (60 MHz maks.) | |||
| Cykle | Czas (μs) | Cykle | Czas (μs) | Cykle | Czas (μs) | |
| 16 bitów | 340 | 17,000 | 343 | 8,575 | 346 | 5,767 |
| 32 bitów | 341,000 | 17,050 | 346,000 | 8,650 | 351,000 | 5,850 |
| Mnożnik zegara pamięci 4 | Mnożnik zegara pamięci 5 | Mnożnik zegara pamięci 6 | ||||
| Dodawanie wektorów | (80 MHz maks.) | (100 MHz maks.) | (120 MHz maks.) | |||
| Cykle | Czas (μs) | Cykle | Czas (μs) | Cykle | Czas (μs) | |
| 16 bitów | 349 | 4,363 | 352 | 3,520 | 352 | 2,933 |
| 32 bitów | 357,000 | 4,464 | 363,000 | 3,630 | 363,000 | 3,025 |






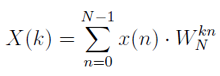
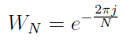
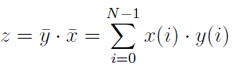
 Caroline Pannier – nowa dyrektorka targów electronica – analizuje sytuację gospodarczą branży i przedstawia wyniki
Caroline Pannier – nowa dyrektorka targów electronica – analizuje sytuację gospodarczą branży i przedstawia wyniki  Konstrukcja Ventiva Zoned Cooling™ – ukierunkowane chłodzenie powietrza dla urządzeń AI Edge
Konstrukcja Ventiva Zoned Cooling™ – ukierunkowane chłodzenie powietrza dla urządzeń AI Edge  Komunikacja dalekiego zasięgu oparta na technologii Qualcomm dla robotyki i dronów
Komunikacja dalekiego zasięgu oparta na technologii Qualcomm dla robotyki i dronów 






