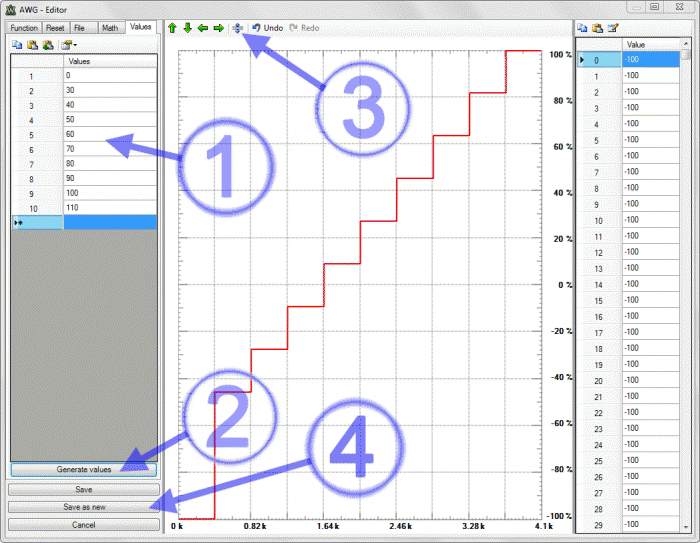
Przebiegu schodkowego nie ma w zestawie sygnałów predefiniowanych generatora arbitralnego. Konieczne więc będzie zaprojektowanie go jako przebiegu użytkownika. Oprogramowanie Digilenta udostępnia do tego kilka metod, my wykorzystamy tabelaryczny opis kształtu. Wybieramy sekwencję przycisków Custom->Edit, w wyniku czego na ekranie zostanie wyświetlony prosty edytor. W rubryce „Values” widocznej w lewej części okna wpisujemy kolejne poziomy schodków (rysunek 5). Na tym etapie projektowania nie są istotne konkretne wartości, ważniejsze są wzajemne relacje między poszczególnymi poziomami. Dla naszych potrzeb wpisujemy kolejno: 0, 30, 40, 50, 60, 70, 80, 90, 100, 110, a następnie wciskamy przycisk Generate Values. Na ekranie ukazuje się przebieg o poziomach zgodnych z wprowadzonymi wartościami, ale nie wypełniający całego obszaru roboczego. Rozciągnięcie go do pełnego zakresu następuje po naciśnięciu przycisku Stretch Vertically. Po wykonaniu tych czynności przebieg może być zapisany na dysku. Ważne jest przyjęcie zasady, aby pierwszy zapis był dokonywany za pomocą komendy Save as new, co zapobiega przed nieumyślnym nadpisaniem poprzednio projektowanego kształtu. Następne operacje zapisu mogą być już bezpiecznie wykonywane komendą Save.

Rys. 5. Okno definiowania przebiegu schodkowego

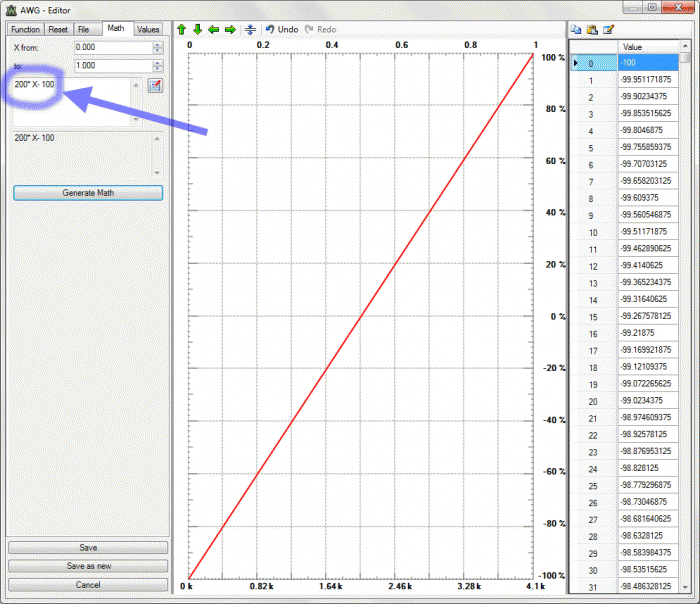
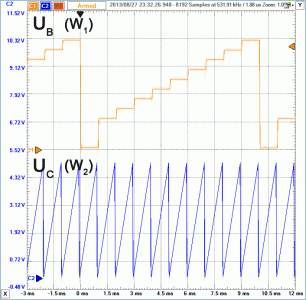
Przechodzimy do kanału 2 generatora arbitralnego (W2), który będzie wytwarzał napięcie podawane przez rezystor R_C na kolektor badanego tranzystora. Napięcie to powinno zmieniać się w całym możliwym do uzyskania zakresie wartości dodatnich. Niestety, ograniczenia sprzętowe zestawu Analog Discovery są tu dość duże. Maksymalne napięcie wyjściowe każdego kanału generatora arbitralnego jest równe tylko 5 V i ta wartość wyznacza zakres zmian napięcia U_CE. Dopuszczalne napięcie U_CE tranzystorów bipolarnych jest większe. Dla uzyskania charakterystyki wyjściowej tranzystora napięcie kolektorowe będzie regulowane liniowo w zakresie od 0 do 5 V. Osiągniemy to projektując odpowiedni przebieg piłokształtny. W tym przypadku najwygodniejszą metodą będzie opis matematyczny przebiegu. Jak wiadomo, funkcja liniowa jest opisana zależnością: y=a·x+b. Współczynnik „a” wyznacza nachylenie wykresu, a „b” określa jego położenie względem zera. Współczynnik „a” jest równy tangensowi kąta nachylenia naszej prostej, a więc: a=(U_MAX-U_MIN)/(t_MAX-t_MIN). I znowu będziemy stosowali umowne jednostki. W oprogramowaniu Digilenta przyjęto, że napięcie przebiegu zmienia się w zakresie od –100 do +100 procent. Różnica między wartością maksymalną a minimalną jest więc równa 200. Każdy przebieg może składać się co najwyżej z 4096 próbek, stąd w oknie edytora oś czasu jest opisana wartościami od 0 do 4,1k (czyli ~4096). Jednak wszystkie te próbki tworzą jeden okres przebiegu, dlatego do obliczeń jako wartość maksymalną na osi czasu należy przyjąć 1. Zgodnie z wcześniej podaną formułą, współczynnik kierunkowy „a” będzie równy: a=200/1=200. Należy jeszcze zauważyć, że w chwili t=0 napięcie wyjściowe ma poziom równy –100, dlatego taką wartość przyjmujemy dla współczynnika „b”. Ostateczna postać formuły opisującej przebieg dla 2 kanału generatora jest więc następująca: y=200*x-100 i taką zależność należy wpisać w polu edycyjnym (rysunek 6). Częstotliwości obu sygnałów dobieramy doświadczalnie. Zauważamy, że jeden „ząb” piłokształtnego przebiegu z kanału 2 przypada na jeden schodek z kanału 1, a ponieważ jest 10 schodków, przyjmujemy np. f1=100 Hz, f2=1 kHz (rysunek 7).

Rys. 6. Okno definiowania przebiegu piłokształtnego

Rys. 7. Zależności czasowe między przebiegami z 1 i 2 kanału generatora arbitralnego

Pozostaje kwestia ustalenia wartości napięć w obu kanałach generatora. W oprogramowaniu Digilenta przyjęto zasadę, że napięcie jest określane parametrami Amplitude i Offset. W naszym eksperymencie założyliśmy, że napięcie najwyższego schodka powinno być równe 2,7 V. Wynikają z tego wartości: Amplitude₁=1,35 V i Offset₁=1,35 V. Napięcie w 2 kanale ma zmieniać się w przedziale od 0 do 5 V, stąd Amplitude₂=2,5 V i Offset₂=2,5 V.

Pomiar

Przyrząd został już przygotowany do pomiaru, można więc powoli przystępować do pracy. Pomiar napięcia U_CE nie sprawi żadnego kłopotu, wystarczy 2 kanał oscyloskopu dołączyć do kolektora tranzystora i do masy. Jak natomiast zmierzyć prąd kolektora? Wykorzystamy do tego bardzo przydatną cechę oscyloskopu wchodzącego w skład zestawu Analog Discovery. Otóż obydwa jego kanały mają wejścia różnicowe oznaczone symbolami „1+”, „1–” dla kanału 1 i „2+”, „2–” dla kanału 2. Oznacza to, że mogą pracować jako typowe wejścia symetryczne, jeśli tylko jedną z końcówek danego kanału dołączymy do masy, ale też możliwy jest pomiar z pływającym potencjałem, bez dołączania końcówek do masy. Jeśli więc drugi kanał dołączymy bezpośrednio do rezystora kolektorowego (rysunek 3), to znając rezystancję R_C będziemy mogli mierzyć prąd kolektora: I_C=U_RC/R_C. Dodatkowo, w celu uzyskania odpowiednio przeliczonych wartości utworzymy wirtualny matematyczny kanał pomiarowy, w którym wielkość wyjściowa jest opisana zależnością: C2/100. C2 oznacza napięcie mierzone w kanale 2, a 100 jest rezystancją rezystora kolektorowego (R_C=100 W). Oś pionowa może być wyskalowana w amperach, z czego oczywiście korzystamy, ponieważ kanał ten oblicza natężenie prądu (rysunek 8).

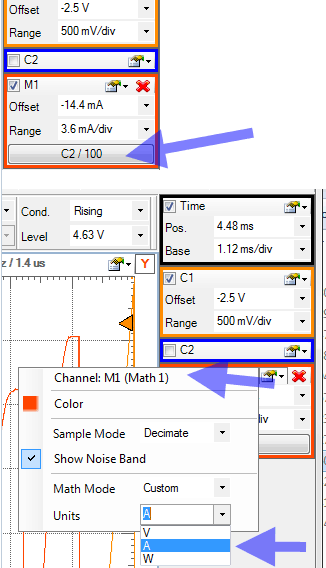
Rys. 8. Ustawienie parametrów wirtualnego kanału matematycznego Math 1