Poradnik LTspice tips&tricks #4 – pomiary harmonicznych
Harmoniczne – odwieczny problem dla ortodoksyjnego audiofila. Audiofil taki kupując wzmacniacz już na wstępie odrzuca oferty na sprzęt, który ma zawartość harmonicznych liczoną w setnych częściach procenta, a nie w tysięcznych. Istne szaleństwo. Czy faktycznie jest to tak ważny parametr? Nie odpowiemy na to pytanie, ale przeprowadzimy kilka eksperymentów z harmonicznymi.
Z teorii opracowanej już w XVIII wieku przez Jeana Baptiste Josepha Fouriera (21.03.1768 – 16.05.1830) wynika, że każdy przebieg okresowy można złożyć z wielu przebiegów sinusoidalnych o odpowiednio dobranych amplitudach i częstotliwościach będących całkowitymi wielokrotnościami częstotliwości podstawowej – tzw. harmonicznych. Wynika z tego ciekawy i bardzo praktyczny wniosek: jeżeli potrafilibyśmy znaleźć wszystkie składowe np. zniekształconej z jakichś powodów sinusoidy, to obliczając ich całkowity udział w odniesieniu do czystego sygnału, moglibyśmy oceniać stopień tego zniekształcenia. Miarą zniekształcenia byłaby zatem zawartość harmonicznych w badanym sygnale.
Są na niej weryfikowane przykłady przedstawione w cyklu artykułów i na filmach. Liczba zestawów Analog Training Board (ATB) dostępnych w cenie promocyjnej jest ograniczona.
Analogowy i cyfrowy pomiar THD
Łatwo powiedzieć, ale jak te składowe znaleźć? W czasach techniki analogowej stosowano przestrajane filtry pasmowo-zaporowe o dużej selektywności. Były one dostrajane do częstotliwości podstawowej i powodowały wycięcie tej składowej z badanego sygnału. W pierwszym kroku filtr był wyłączany, mierzony był więc poziom całego sygnału, tzn. składowej podstawowej wraz ze wszystkimi harmonicznymi. Analogowe przyrządy przeznaczone do pomiaru zniekształceń były zwykle wyposażane w potencjometr kalibrujący i odpowiednio wyskalowany miernik wskazówkowy. Przed pomiarem zasadniczym operator tak ustawiał wzmocnienie, aby wskazówka wychylała się do końca skali na wartość „1”. Następnie włączany był filtr wycinający z sygnału składową o częstotliwości podstawowej. Wskazanie miernika spadało i odpowiadało w tym momencie zawartości harmonicznych w całym sygnale. Miernik skalowano w procentach. Zawartość harmonicznych mierzona tą metodą była definiowana zależnością:
Jak się okazuje, XVIII-wieczne zasługi Fouriera były dużo większe. Wraz z pojawieniem się techniki cyfrowej zyskaliśmy bardzo potężne narzędzia matematyczne używane do obróbki sygnałów. Przekształcenia matematyczne wyprowadzone przez Fouriera w czasach, gdy nie miał on pojęcia, że kiedykolwiek ludzie będą używać czegoś takiego jak mikroprocesor, stanowią dzisiaj podstawowe narzędzie m.in. w technice pomiarowej. Za pomocą transformaty Fouriera, przy zastosowaniu algorytmu FFT, potrafimy niemal w czasie rzeczywistym rozkładać sygnały na składowe harmoniczne. Mamy więc na wyciągnięcie ręki obliczenie współczynnika zawartości harmonicznych. Współczynnik zawartości harmonicznych liczony tą techniką zwykle definiujemy nieco inaczej. Udział harmonicznych nie jest odnoszony do pełnego sygnału, a tylko do składowej podstawowej. Tak obliczany współczynnik czasami jest oznaczany indeksem F.
Artykuł jest częścią pełnego kursu obsługi symulatora układów elektronicznych LTspice pt. „LTspice tips&tricks”. Kurs składa się z 10 części:
- Jak używać w symulacjach sygnałów zewnętrznych oraz jak w układach rzeczywistych korzystać z sygnałów wytwarzanych przez symulator
- Pomiary wzmacniacza standardowego i rail-to-rail
- Strojone filtry dolno- i górnoprzepustowe
- Pomiary harmonicznych – czytasz ten artykuł
- Symulacja metodą Monte Carlo i Worst Case
- Scrambler audio: odwracanie widma i kilka innych tricków
- Tajniki próbkowania (aliasing) sygnałów analogowych
- Wzmacniacze pomiarowe,
- Wzmacniacz tranzystorowy w układzie ze wspólnym emiterem (OE)
- LTspice jako narzędzie przydatne w obliczeniach transmitancji
Każdy odcinek ukazał się także w wersji wideo. Materiały te dostępne są na portalu YouTube
Jak powstają harmoniczne?
Wiemy już, że harmoniczne powstają w przypadku, gdy czysty sygnał sinusoidalny zostanie z jakichkolwiek powodów zniekształcony. Zniekształcenia takie powstają zawsze, gdy w torze obróbki sygnału analogowego pojawią się jakieś nieliniowości. Na rys. 1 przedstawiono na przykład charakterystykę Ic=f(UBE) tranzystora użytego we wzmacniaczu sygnału sinusoidalnego. Na etapie projektowania ustalany jest punkt pracy określający wszystkie prądy i napięcia występujące w układzie w warunkach bez wysterowania. Na rys. 1 jest to punkt oznaczony symbolem „PP”. Jeżeli tranzystor ten wysterujemy sygnałem pokazanym na wykresie jako czerwona sinusoida, to dodatnia połówka będzie wzmacniana na odcinku „A” charakterystyki znajdującym się powyżej punktu „PP”. Można uznać, że jest to odcinek liniowy. Dodatnia połówka będzie więc wzmacniana bez zniekształceń. Dolna połówka przypada natomiast na nieliniowe kolano charakterystyki, co spowoduje widoczne na rys. 1. zniekształcenia (punkty 8, 9, 10, 11 i 12). Sygnał wyjściowy tak zaprojektowanego wzmacniacza na pewno będzie charakteryzował się dużą zawartością harmonicznych.
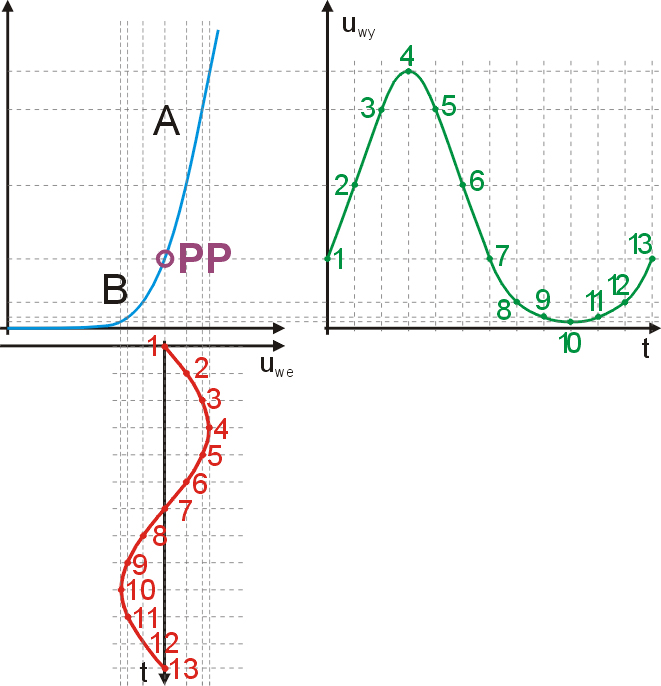 Rys. 1. Charakterystyka Ic=f(UBE) tranzystora z zaznaczonym punktem pracy
Rys. 1. Charakterystyka Ic=f(UBE) tranzystora z zaznaczonym punktem pracy
Czy THD jest obiektywnym wskaźnikiem zniekształceń?
Zniekształcenia są mierzone w wielu różnych rodzajach urządzeń elektronicznych, ale ich istnienie jest chyba najbardziej odczuwalne w sprzęcie audio. Czy zatem dwa wzmacniacze o jednakowym THD grają tak samo? To znaczy, czy subiektywne odczucia przy ich słuchaniu są jednakowe?
Wykonamy eksperyment, w którym do źródła czystego sygnału sinusoidalnego o częstotliwości 440 Hz dodamy dwie harmoniczne. Rozpatrzymy dwa przypadki: w pierwszym dodamy 2. harmoniczną o poziomie 10% składowej podstawowej i 7. harmoniczną o poziomie 5%. W drugim zaś przypadku odwrotnie: 2. harmoniczna ma poziom 5%, a 7. harmoniczna 10% (rys. 2). Z założeń tych wynika, że oba przebiegi zniekształcone mają tę samą zawartość harmonicznych, a po prostych obliczeń okazuje się, że THDF jest dla nich równy ok. 11%.
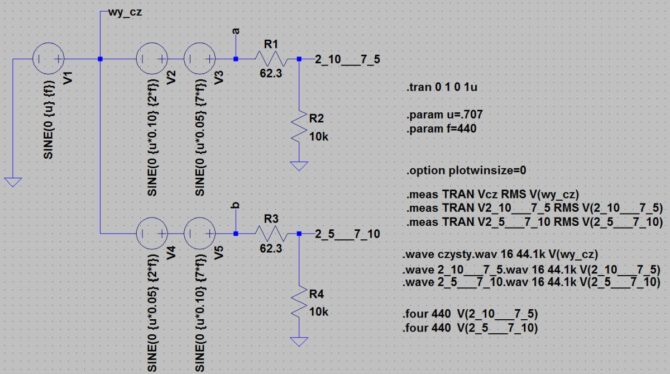 Rys. 2. Układ symulujący zniekształcenia harmoniczne
Rys. 2. Układ symulujący zniekształcenia harmoniczne
Sygnały zniekształcone są wyprowadzone na wyjścia odpowiednio: „2_10___7_5” i „3_5___7_10” za pośrednictwem dzielników napięciowych wyrównujących wszystkie napięcia wyjściowe do jednakowego poziomu. Wartości RMS tych napięć są mierzone poleceniami:
.meas TRAN Vcz RMS V(wy_cz) .meas TRAN V2_10___7_5 RMS V(2_10___7_5) .meas TRAN V2_5___7_10 RMS V(2_5___7_10)
Mierzymy też harmoniczne na wyjściach sygnałów odkształconych:
.four 440 V(2_10___7_5) .four 440 V(2_5___7_10)
W wyniku symulacji program tworzy ponadto pliki WAV zawierające sygnały ze wszystkich wyjść. Po zakończeniu obliczeń można je odsłuchać, aby stwierdzić czy brzmią jednakowo. Na rys. 3 przedstawiono wyniki pomiaru harmonicznych, współczynników THD i napięć RMS.
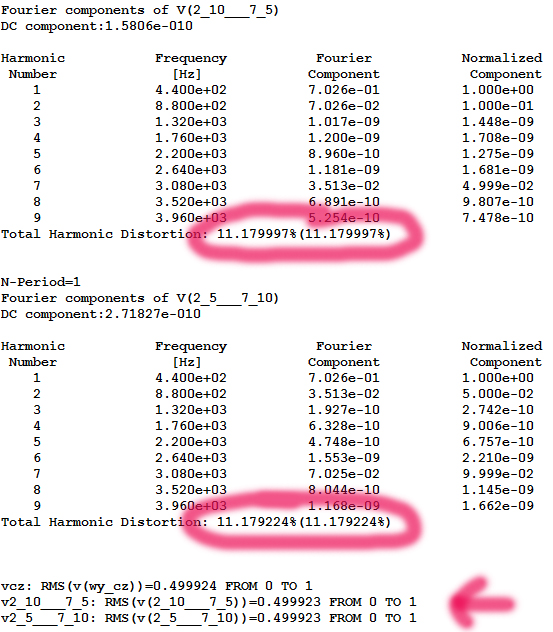 Rys. 3. Wyniki pomiarów THD i URMS
Rys. 3. Wyniki pomiarów THD i URMS
Prawdopodobnie dla większości osób dźwięki wygenerowane w symulacji będą się różniły w odsłuchu. Na pewno łatwe do rozróżnienia będą sygnały czyste od zniekształconych, ale nawet oba sygnały zniekształcone też będą różniły się w subiektywnym odbiorze. A przecież w obu przypadkach współczynnik zawartości harmoniczny jest taki sam.
Analogiczny eksperyment w układzie rzeczywistym
Tym razem te same dźwięki wygenerujemy nie na drodze symulacji, tylko w układzie rzeczywistym. Użyjemy do tego generatora arbitralnego Analog Discovery 2 pracującego w trybie „Custom”. Definiujemy w nim 3 przebiegi użytkownika za pomocą wyrażeń matematycznych:
- przebieg 2_5___7_10: sin(2*PI*X)+.05*sin(2*PI*2*X) +.10*sin(2*PI*7*X),
- przebieg 2_10___7_5: (sin(2*PI*X)+.10*sin(2*PI*2*X) +.5*sin(2*PI*7*X))*.949,
- czysty przebieg: (sin(2*PI*X)*.959.
Po wpisaniu formuł w oknie skryptu należy wygenerować przebiegi, do czego służy przycisk Generate. W pierwszym przypadku operację tę należy wykonać z zaznaczoną opcją „Normalize”. W dwóch kolejnych musi być ona wyłączona, gdyż stosujemy własne współczynniki normalizujące. Są to czynniki dopisane na końcu wyrażeń i zapewniające równość napięć RMS wszystkich generowanych sygnałów.
Gdy wszystkie definicje są już gotowe można przystąpić do odsłuchu. Słuchawki dołączamy do wejścia słuchawkowego Analog Discovery 2. Jest ono umieszczone po prawej stronie gniazda USB. Zamiast słuchawek można dołączyć przewód doprowadzający sygnał z AD2 do wejścia dowolnego wzmacniacza akustycznego i słuchać w głośnikach.
Przesterowanie wzmacniacza
Każdy wzmacniacz, choćby nie wiadomo jakiej był jakości, zacznie wytwarzać spore ilości harmonicznych jeśli zostanie przesterowany. W kolejnym eksperymencie spróbujemy wykryć moment przesterowania wzmacniacza. Będzie nim wzmacniacz operacyjny ADA4622 znajdujący się na płytce Analog Training Board – ten sam, który mierzyliśmy porównując wzmacniacz operacyjny rail-to-rail ze wzmacniaczem standardowym. Ma on wzmocnienie 10 i pracuje w konfiguracji z wejściem odwracającym. W celu zgrubnego oszacowania liniowego zakresu pracy wzmacniacza przeprowadzimy symulację DC, która utworzy charakterystykę przejściową (rys. 4). Symulację uruchamiamy poleceniem:
.dc V1 -1 1 1m
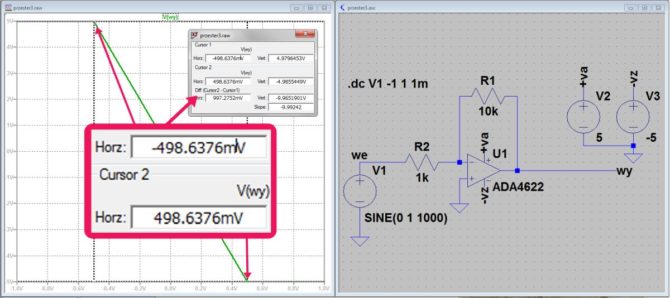 Rys. 4. Pomiar charakterystyki przejściowej wzmacniacza ADA4622
Rys. 4. Pomiar charakterystyki przejściowej wzmacniacza ADA4622
Napięcie wejściowe zmienia się od –1 V do 1 V z krokiem 1 mV i dla każdej wartości obliczane jest napięcie wyjściowe. Na tej podstawie program rysuje charakterystykę przejściową. Korzystając z kursorów pomiarowych odczytujemy, że załamanie charakterystyki następuje przy napięciu wejściowym ok. 498 mV.
Nietypowa metoda wyznaczania momentu wejścia w stan przesterowania wzmacniacza
Tym razem wzmacniacz sterujemy napięciem sinusoidalnym o amplitudzie zmieniającej się od 350 mV do 550 mV (rys. 5). Jest ona w symulacji zadana parametrycznie poleceniem:
.step param um 350m 550m 1m
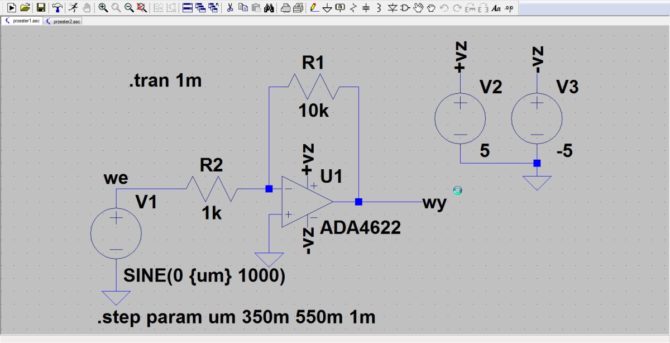 Rys. 5. Pomiar odpowiedzi wzmacniacza na pobudzanie sygnałem sinusoidalnym o różnych amplitudach
Rys. 5. Pomiar odpowiedzi wzmacniacza na pobudzanie sygnałem sinusoidalnym o różnych amplitudach
Napięcie 350 mV jest bezpieczne, zawiera się w liniowym odcinku pracy wzmacniacza i na pewno będzie wzmacniane bez zniekształceń, ale wiadomo już, że w którymś momencie wzmacniacz zostanie przesterowany.
Uruchamiamy symulację czasową .tran 1m, wskazujemy wyjście jako punkt z którego należy pobrać napięcie do wykresu i obserwujemy je. Symulacja trwa chwilę. Po zakończeniu obliczeń powinien ukazać się wykres jak na rys. 6. Teraz zastosujemy nietypowy zabieg polegający na zmianie danych do wykresu. Od napięcia wyjściowego odejmiemy 10-krotnie powiększone napięcie wejściowe. Liczba 10 to wzmocnienie układu. W wyniku takiej operacji powinniśmy uzyskać zero. Pamiętamy jednak, że wzmacniacz pracuje w konfiguracji odwracającej fazę, więc odjęcie wzmocnionego sygnału wejściowego od wyjściowego będzie oznaczało w zapisie matematycznym wykonanie operacji dodawania.
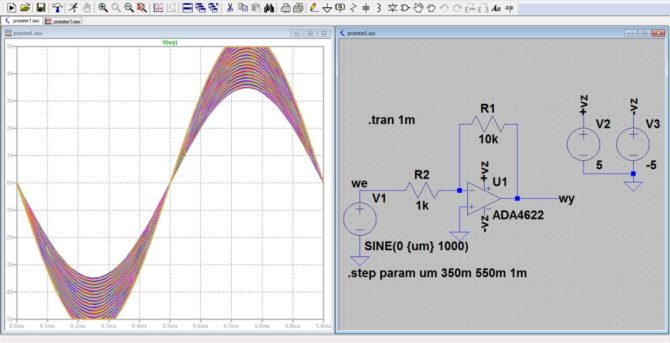 Rys. 6. Przebiegi wyjściowe wzmacniacza sterowanego sygnałem sinusoidalnym o różnych amplitudach
Rys. 6. Przebiegi wyjściowe wzmacniacza sterowanego sygnałem sinusoidalnym o różnych amplitudach
Pomiar progu przesterowania wzmacniacza
Klikamy prawym przyciskiem myszki na opis wykresu widniejący nad nim i w polu edycji wprowadzamy formułę: V(wy)+10*V(we) – rys. 7. Po jej zaakceptowaniu wykres zmienia kształt (rys. 8). Naprowadzamy kursor pomiarowy na środek jednego z dwóch listków i naciskamy prawy przycisk myszki. W okienku pomiarowym pojawiają się dane dla wybranego aktualnie napięcia wejściowego. Na początku będzie to pierwsze napięcie podawane na wejście wzmacniacza, czyli 350 mV. Naciskając przycisk “Kursor w górę” na klawiaturze komputera powodujemy przechodzenie do następnego napięcia wejściowego. Powtarzamy tę czynność dotąd, aż kursor pomiarowy zacznie podchodzić do góry. Moment, w którym to się dzieje odpowiada wejściu w stan przesterowania, gdyż pojawia się różnica między sygnałem wyjściowym a wzmocnionym sygnałem wejściowym. W naszym przypadku jest to napięcie 498 mV, a więc zbliżone do tego, które określiliśmy na podstawie załamania charakterystyki przejściowej.
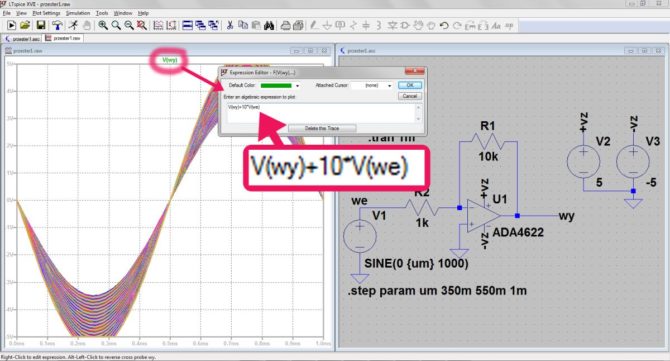 Rys. 7. Edycja formuły wykresu wyświetlanego w oknie wynikowym
Rys. 7. Edycja formuły wykresu wyświetlanego w oknie wynikowym
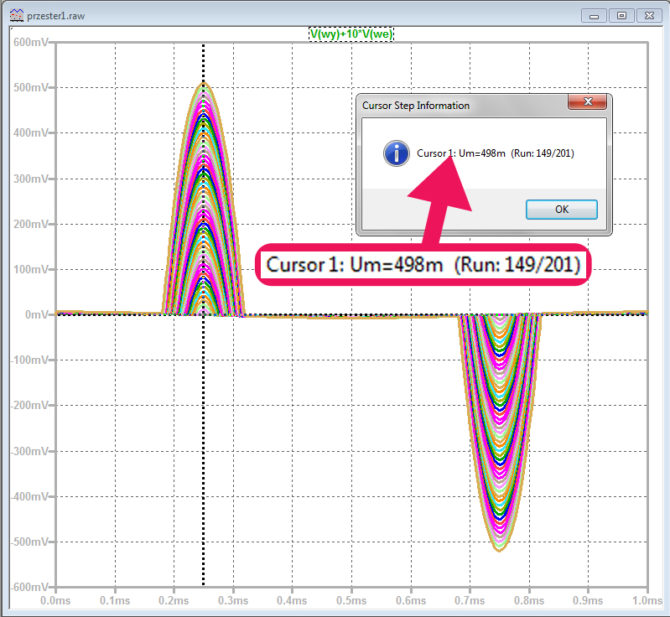 Rys. 8. Zmodyfikowany wykres w oknie wynikowym
Rys. 8. Zmodyfikowany wykres w oknie wynikowym
Wyznaczenie momentu wejścia w stan przesterowania wzmacniacza rzeczywistego
W pomiarze układu rzeczywistego zastosujemy dokładnie tę samą metodę. Płytkę Analog Training Board konfigurujemy tak, jak to pokazano na rys. 9. Uruchamiamy program WaveForms, a w nim generator arbitralny, oscyloskop i analizator widma (narzędzie Spectrum)). Ustawiamy w 1. kanale generatora sygnał sinusoidalny o częstotliwości 449 Hz i amplitudzie 350 mV. W oscyloskopie definiujemy kanał matematyczny klikając prawym przyciskiem myszki w polu pod parametrami kanałów pomiarowych i wybierając opcję „Custom”. Klikamy na aktualną formułę matematyczną przypisaną do tego kanału, która jest widoczna w dolnej części parametrów kanału „Math 1”. Zmieniamy ją na: C2+10*C1.
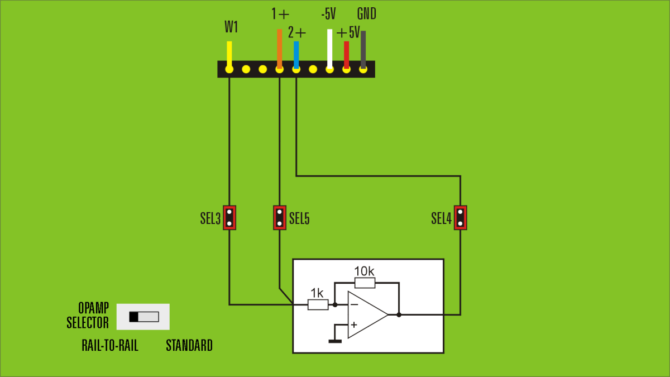 Rys. 9. Konfiguracja płytki Analog Training Board do pomiaru zniekształceń harmonicznych wzmacniacza ADA4622
Rys. 9. Konfiguracja płytki Analog Training Board do pomiaru zniekształceń harmonicznych wzmacniacza ADA4622
Ponieważ wskazania tego kanału będą dość mocno zaszumione, tworzymy kanał filtrujący. Postępujemy podobnie, tylko zamiast opcji „Custom” wybieramy „Filter”. Wybieramy dla niego opcje: Filter=Butherworth, Order=2, Type=Low-pass, Freqq1=10kHz. Przypisujemy go do kanału M1.
Podczas pomiarów wzmacniacza kanał „Math 1” można wyłączyć (ale nie usunąć), aby nie zaciemniał oscylogramów. My obserwujemy kanał filtru, zwracając szczególną uwagę na dwa punkty jego wykresu (rys. 10). W chwili wchodzenia w stan przesterowania na skutek zwiększania napięcia wejściowego, pojawią się w tych punktach wyraźne załamania świadczące o tym, że występują różnice między rzeczywistym sygnałem wyjściowym a teoretycznie wzmocnionym wejściowym. Jest to analogiczna sytuacja, jaką obserwowaliśmy podczas symulacji. Co ciekawe, pomiar THD za pomocą analizatora widma (Spectrum) nie wykazuje jeszcze w tym momencie żadnych zmian (rys. 11). Harmoniczne zaczynają gwałtownie narastać dopiero po wyraźnym przejściu przez kolano charakterystyki przejściowej.
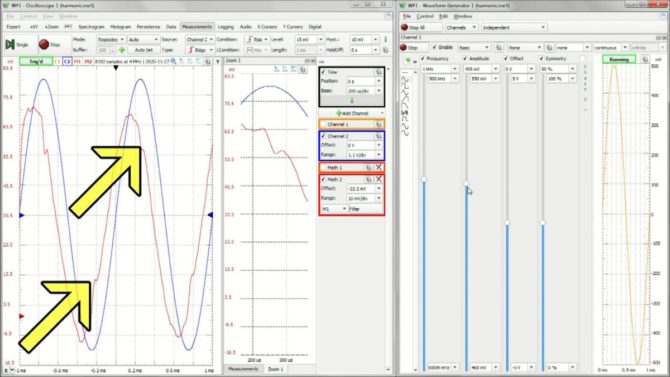 Rys. 10. Charakterystyczne punkty oscylogramu, w których występują załamania w chwili wchodzenia w stan przesterowania wzmacniacza
Rys. 10. Charakterystyczne punkty oscylogramu, w których występują załamania w chwili wchodzenia w stan przesterowania wzmacniacza
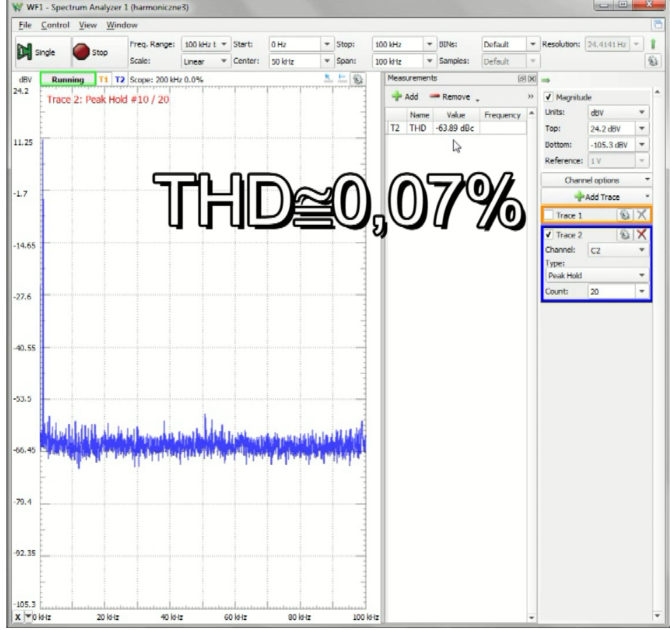 Rys. 11. Wynik pomiaru THD wzmacniacza za pomocą analizatora widma Analog Discovery 2
Rys. 11. Wynik pomiaru THD wzmacniacza za pomocą analizatora widma Analog Discovery 2






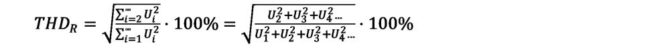
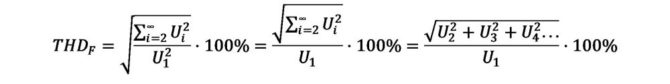
 Caroline Pannier – nowa dyrektorka targów electronica – analizuje sytuację gospodarczą branży i przedstawia wyniki
Caroline Pannier – nowa dyrektorka targów electronica – analizuje sytuację gospodarczą branży i przedstawia wyniki  Konstrukcja Ventiva Zoned Cooling™ – ukierunkowane chłodzenie powietrza dla urządzeń AI Edge
Konstrukcja Ventiva Zoned Cooling™ – ukierunkowane chłodzenie powietrza dla urządzeń AI Edge  Komunikacja dalekiego zasięgu oparta na technologii Qualcomm dla robotyki i dronów
Komunikacja dalekiego zasięgu oparta na technologii Qualcomm dla robotyki i dronów 






