Poradnik LTspice tips & tricks #10 – LTspice jako narzędzie przydatne w obliczeniach transmitancji
W tym odcinku będzie spora dawka dość złożonych obliczeń. Przypomnimy sobie metody rozwiązywania obwodów elektrycznych. Do zrozumienia przedstawionych zagadnień bardzo przydatna, wręcz wymagana jest elementarna wiedza z teorii obwodów.
Naszym zadaniem będzie obliczenie transmitancji pewnego obwodu elektrycznego o pozornie nieokreślonym przeznaczeniu i wykreślenie jego charakterystyki amplitudowej. Obliczenia tego typu, nawet w przypadku względnie prostych obwodów stają się dość złożone. Łatwo można popełnić błąd, którego wyszukanie zajmie sporo czasu. Często tak ulegamy własnej sugestii, że nawet wielokrotnie przeprowadzona analiza nie daje później żadnego rezultatu. Najprostszą metodą sprawdzenia własnych obliczeń i ewentualnej lokalizacji błędów jest zastosowanie jakiegoś niezależnego narzędzia. Jest nim na przykład symulator LTspice.
Zagadnienie do rozwiązania
Obwód, którego transmitancję policzymy nie ma żadnych własności użytkowych. W tym przypadku nie chodzi nam o to, by uporać się z jakimś konkretnym zagadnieniem technicznym, lecz o to, by pokazać jedną z wielu metod rozwiązania problemów związanych z teorią obwodów. Mamy więc piramidę zbudowaną z elementów R, L i C przedstawioną na rysunku 1. Wszystkie boki tej piramidy mają kształt trójkąta, a każdy z nich zawiera trzy różne elementy. Dla uproszczenia obliczeń przyjmujemy, że elementy poszczególnych typów mają równe wartości, i tak: R=1 Ω , L=4,5 μH i C=100 nF. Sygnał wejściowy jest doprowadzony do wierzchołka A podstawy piramidy, wyjście jest w wierzchołku B, a wierzchołek C jest dołączony do punktu odniesienia – masy.
 Rysunek 1. Rozpatrywany układ w konfiguracji piramidy
Rysunek 1. Rozpatrywany układ w konfiguracji piramidy
Są na niej weryfikowane przykłady przedstawione w cyklu artykułów i na filmach. Liczba zestawów Analog Training Board (ATB) dostępnych w cenie promocyjnej jest ograniczona.
Układ jest na pierwszy rzut oka dość nieprzyjemny do obliczeń. Z każdego węzła odchodzą 3 rozgałęzienia, nie da się więc go zwinąć prostymi metodami. Obecność trójkątów nasuwa pomysł, aby skorzystać z przekształceń trójkąt-gwiazda. Zasadę tę przedstawiono na rysunku 2, a na rysunku 3 widoczne są kolejne etapy zwijania obwodu.
 Rysunek 2. Ilustracja zasady przekształcania trójkąt-gwiazda
Rysunek 2. Ilustracja zasady przekształcania trójkąt-gwiazda
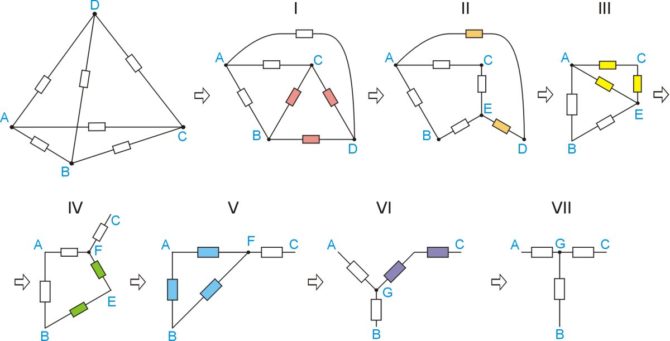 Rysunek 3. Kolejne etapy zwijania układu z zastosowaniem przekształcenia trójkąt-gwiazda
Rysunek 3. Kolejne etapy zwijania układu z zastosowaniem przekształcenia trójkąt-gwiazda
Artykuł jest częścią pełnego kursu obsługi symulatora układów elektronicznych LTspice pt. „LTspice tips&tricks”. Kurs składa się z 10 części:
- Jak używać w symulacjach sygnałów zewnętrznych oraz jak w układach rzeczywistych korzystać z sygnałów wytwarzanych przez symulator
- Pomiary wzmacniacza standardowego i rail-to-rail
- Strojone filtry dolno- i górnoprzepustowe
- Pomiary harmonicznych
- Symulacja metodą Monte Carlo i Worst Case
- Scrambler audio: odwracanie widma i kilka innych tricków
- Tajniki próbkowania (aliasing) sygnałów analogowych
- Wzmacniacze pomiarowe,
- Wzmacniacz tranzystorowy w układzie ze wspólnym emiterem (OE)
- LTspice jako narzędzie przydatne w obliczeniach transmitancji – czytasz ten artykuł
Każdy odcinek ukazał się także w wersji wideo. Materiały te dostępne są na portalu YouTube
Analiza układu metodą Thevenina
No cóż, do uzyskania końcowego obwodu, z którego już bez większego problemu będzie możliwe obliczenie transmitancji wymaga wykonania aż 7 kroków. Gdyby piramida składała się z samych rezystorów można by ewentualnie zdecydować się na taką metodę obliczeń, my mamy jednak elementy R, L i C, więc obliczenia znacznie się skomplikują. Zastosujemy więc metodę Thevenina, w której będziemy zwijać układ wprowadzając źródła zastępcze. W tym celu przerysujemy schemat piramidy nieco inaczej, wydzielając dwa obwody, które będą analizowane niezależnie (rysunek 4). Są one zasilane dwoma źródłami napięciowymi o tym samym napięciu U1. Możemy tak postąpić, ponieważ wejściami obwodu górnego i dolnego jest ten sam punkt oznaczony literką A.
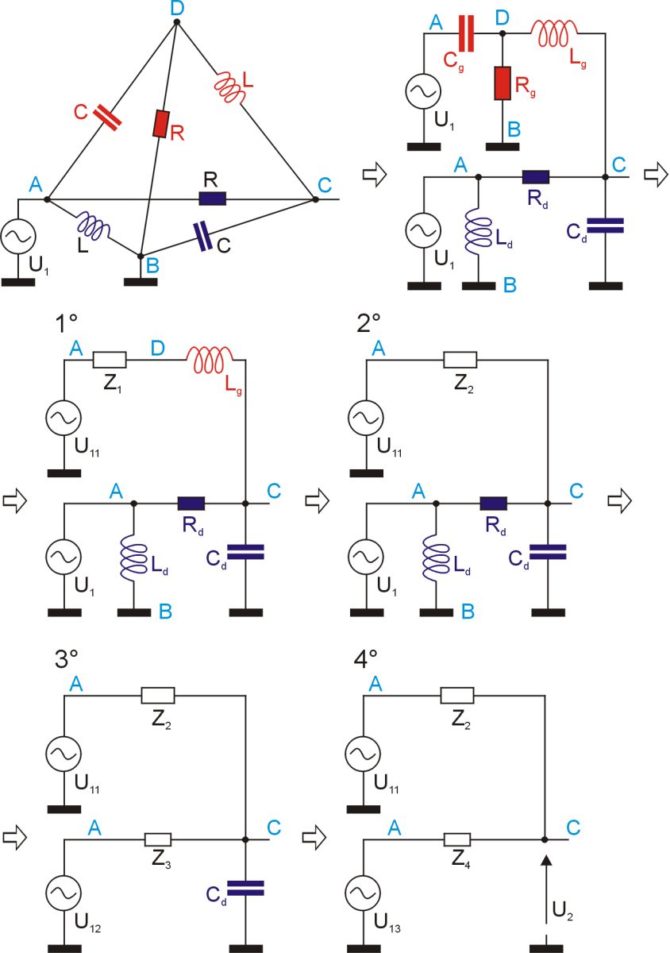 Rysunek 4. Kolejne etapy zwijania układu z zastosowaniem metody Thevenina
Rysunek 4. Kolejne etapy zwijania układu z zastosowaniem metody Thevenina
Najpierw rozpatrzymy obwód górny. Utworzymy źródło zastępcze dla U1 uwzględniające elementy Cg i Rg. Napięcie tego źródła jest równe napięciu, jakie występuje na rezystorze Rg. Będzie ono niższe od U1, gdyż elementy Cg i Rg tworzą dzielnik napięciowy. Ze względu na to, że w obwodzie występują elementy reaktancyjne, do obliczeń zastosujemy rachunek operatorowy, w którym reaktancja kondensatora jest równa 1/(s*C), a reaktancja cewki s*L. Napięcie tak utworzonego źródła zastępczego jest więc równe:
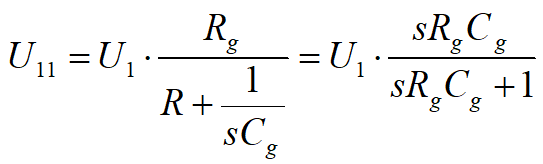 Indeksy do elementów dodano tylko w celu rozróżnienia ich na schemacie. Impedancja zastępcza Z11 źródła jest równa równoległemu połączeniu elementów Rg i Cg:
Indeksy do elementów dodano tylko w celu rozróżnienia ich na schemacie. Impedancja zastępcza Z11 źródła jest równa równoległemu połączeniu elementów Rg i Cg:
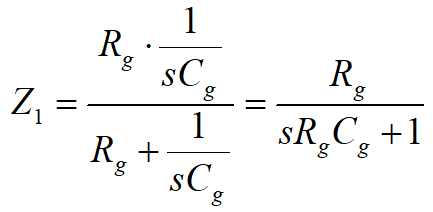 W tym kroku analizujemy tylko górną część obwodu. Napięcie w punkcie C jest równe napięciu źródła zastępczego U11. Jego impedancja wewnętrzna natomiast zwiększy się o reaktancję cewki Lg:
W tym kroku analizujemy tylko górną część obwodu. Napięcie w punkcie C jest równe napięciu źródła zastępczego U11. Jego impedancja wewnętrzna natomiast zwiększy się o reaktancję cewki Lg:
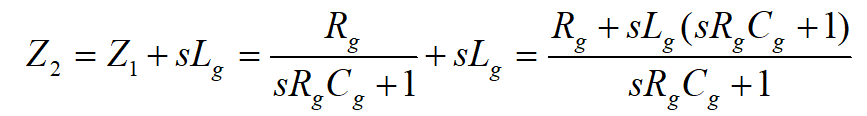
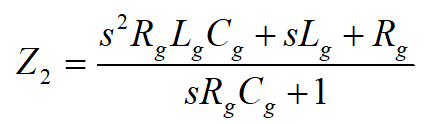 Obwód dolny
Obwód dolny
W kolejnym kroku (3°) zajmiemy się obwodem dolnym. Utworzymy źródło zastępcze zbudowane z elementów U1 (dolne), Ld i Rd. W tym przypadku nie ma żadnych dzielników napięciowych, więc napięcie U12 jest równe U1. Impedancja zastępcza tego źródła jest równa rezystancji R, gdyż idealne źródło U1 zwiera cewkę Ld. Mamy więc:
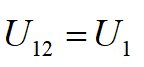
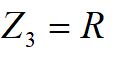 Do dalszych obliczeń konieczne jest jeszcze kolejne zwinięcie obwodu dolnego. W kroku 4° tworzymy więc źródło zastępcze składające się z elementów U12, Z3 i Cd. Napięcie U13 jest równe:
Do dalszych obliczeń konieczne jest jeszcze kolejne zwinięcie obwodu dolnego. W kroku 4° tworzymy więc źródło zastępcze składające się z elementów U12, Z3 i Cd. Napięcie U13 jest równe:
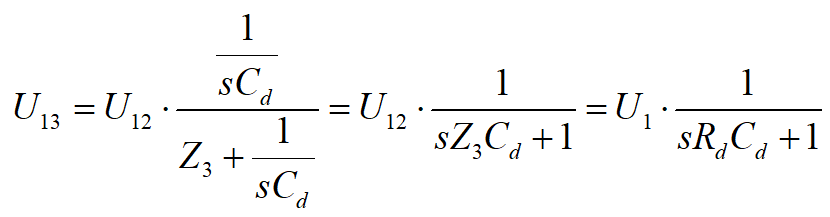 a impedancja wewnętrzna Z4 tego źródła jako równoległe połączenie Z3 i reaktancji kondensatora Cd jest równa:
a impedancja wewnętrzna Z4 tego źródła jako równoległe połączenie Z3 i reaktancji kondensatora Cd jest równa:
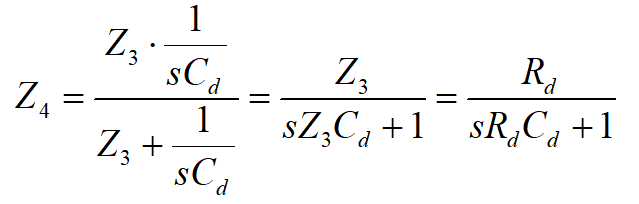 W wyniku przeprowadzonych operacji uzyskaliśmy obwód składający się z dwóch źródeł napięciowych U11 i U13 oraz dwóch impedancji Z2 i Z4. Napięcie wyjściowe U2 obliczymy korzystając z zasady superpozycji. W tym celu najpierw zwieramy źródło U11 i obliczamy napięcie wyjściowe U21, następnie zwieramy źródło napięciowe U13 i obliczamy napięcie U22. Całkowite napięcie wyjściowe będzie równe sumie napięć U21 i U22. We wszystkich powyższych wyrażeniach występuje czynnik RC będący stałą czasową obwodu RC. Jest on oznaczany zwykle literką τ, którą zastosujemy w następnych obliczeniach. Korzystając z zależności, że Rd=Rg=R, Ld=Lg=L i Cd=Cg=C można napisać:
W wyniku przeprowadzonych operacji uzyskaliśmy obwód składający się z dwóch źródeł napięciowych U11 i U13 oraz dwóch impedancji Z2 i Z4. Napięcie wyjściowe U2 obliczymy korzystając z zasady superpozycji. W tym celu najpierw zwieramy źródło U11 i obliczamy napięcie wyjściowe U21, następnie zwieramy źródło napięciowe U13 i obliczamy napięcie U22. Całkowite napięcie wyjściowe będzie równe sumie napięć U21 i U22. We wszystkich powyższych wyrażeniach występuje czynnik RC będący stałą czasową obwodu RC. Jest on oznaczany zwykle literką τ, którą zastosujemy w następnych obliczeniach. Korzystając z zależności, że Rd=Rg=R, Ld=Lg=L i Cd=Cg=C można napisać:
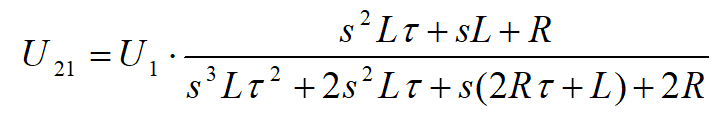 Nie wygląda to najlepiej, ale na razie zostawiamy to wyrażenie w takiej postaci. A teraz liczymy U22:
Nie wygląda to najlepiej, ale na razie zostawiamy to wyrażenie w takiej postaci. A teraz liczymy U22:
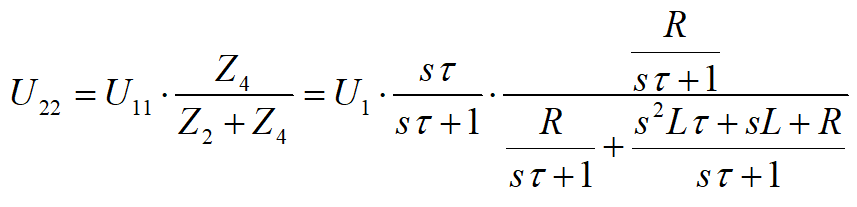
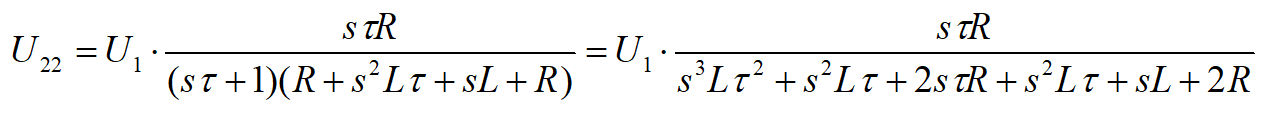
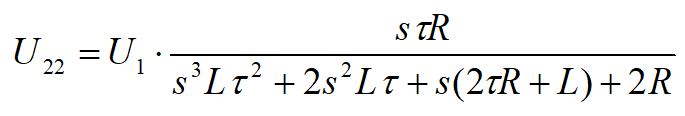 Mamy już dwa składniki, z których obliczamy całkowite napięcie wyjściowe U2.
Mamy już dwa składniki, z których obliczamy całkowite napięcie wyjściowe U2.
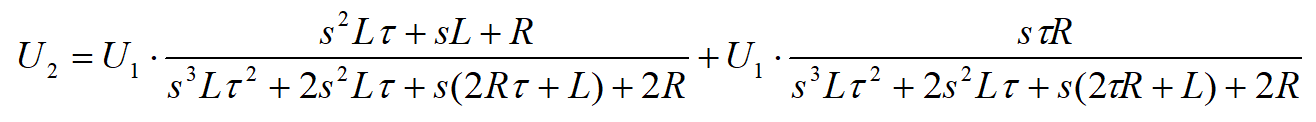
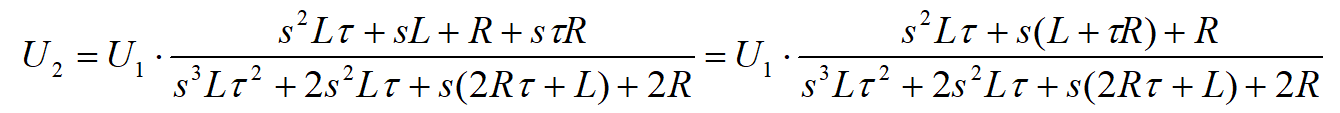 Transmitancja układu
Transmitancja układu
Transmitancja układu jest równa stosunkowi napięcia wyjściowego do wejściowego, a więc:
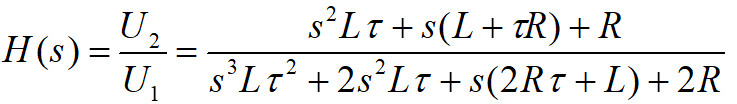 Otrzymaliśmy wyrażenie opisujące transmitancję układu. Właściwie można by zakończyć na tym działania, ale powyższy wzór nie jest zbyt czytelny, spróbujemy jeszcze coś z nim zrobić. Intuicja nakazuje podzielenie licznika i mianownika przez sτ+1. Czy ktoś jeszcze pamięta dzielenie wielomianów? Jeśli nie, to jest dobry moment do przypomnienia sobie. Najpierw licznik.
Otrzymaliśmy wyrażenie opisujące transmitancję układu. Właściwie można by zakończyć na tym działania, ale powyższy wzór nie jest zbyt czytelny, spróbujemy jeszcze coś z nim zrobić. Intuicja nakazuje podzielenie licznika i mianownika przez sτ+1. Czy ktoś jeszcze pamięta dzielenie wielomianów? Jeśli nie, to jest dobry moment do przypomnienia sobie. Najpierw licznik.
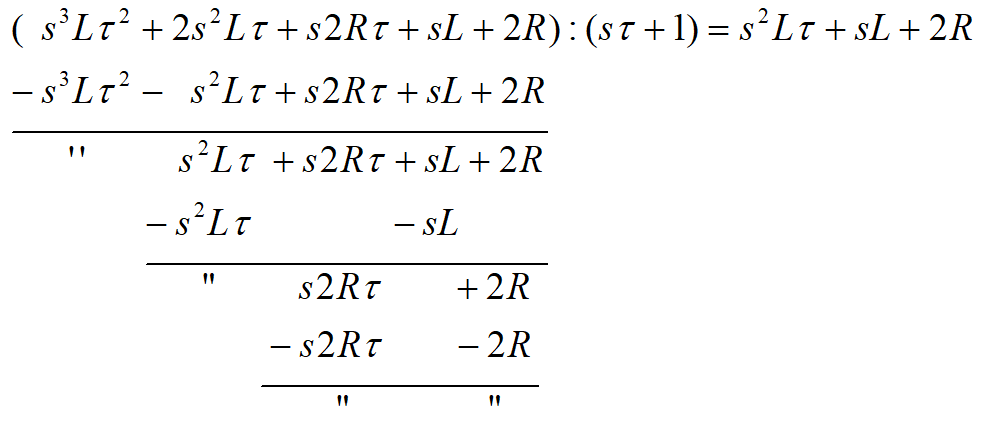 Po podzieleniu licznika i mianownika transmitancji przez sτ+1 wyrażenie znacznie się uprościło i wygląda jak niżej:
Po podzieleniu licznika i mianownika transmitancji przez sτ+1 wyrażenie znacznie się uprościło i wygląda jak niżej:
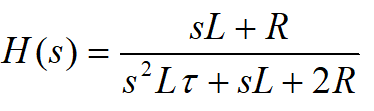 Podzielmy jeszcze licznik i mianownik przez 2R.
Podzielmy jeszcze licznik i mianownik przez 2R.
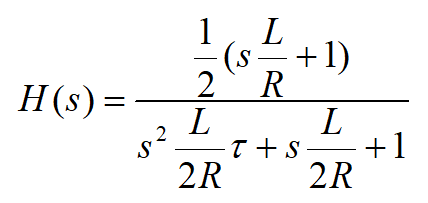 w równaniu pojawiły się kolejne dwie stałe czasowe:
w równaniu pojawiły się kolejne dwie stałe czasowe:
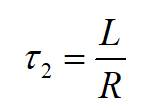
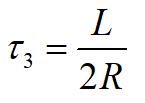 Transmitancja przyjmuje więc ostateczną postać:
Transmitancja przyjmuje więc ostateczną postać:
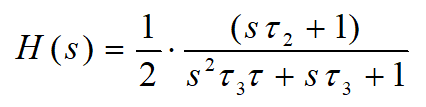 Taka postać transmitancji pozwala już powiedzieć niemal wszystko o naszej piramidzie. Po pierwsze, dla prądu stałego i małych częstotliwości transmitancja jest równa 1/2 (-6 dB), wiec na wyjściu wystąpi połowa napięcia wejściowego. Po drugie, mamy jedno zero i dwa bieguny, więc charakterystyka amplitudowa będzie miała jedno zagięcie do góry i dwa zagięcia na dół. Każde zagięcie powoduje zmianę nachylenia charakterystyki amplitudowej o 20 db/dek do góry dla zera i tyle samo na dół dla bieguna. W szczególnym przypadku może wystąpić jeden podwójny biegun dla którego charakterystyka zagnie się o 40 db/dek na dół. Będzie to zależało od wartości elementów. Warto więc sprawdzić jak wygląda charakterystyka naszego fizycznego układu.
Taka postać transmitancji pozwala już powiedzieć niemal wszystko o naszej piramidzie. Po pierwsze, dla prądu stałego i małych częstotliwości transmitancja jest równa 1/2 (-6 dB), wiec na wyjściu wystąpi połowa napięcia wejściowego. Po drugie, mamy jedno zero i dwa bieguny, więc charakterystyka amplitudowa będzie miała jedno zagięcie do góry i dwa zagięcia na dół. Każde zagięcie powoduje zmianę nachylenia charakterystyki amplitudowej o 20 db/dek do góry dla zera i tyle samo na dół dla bieguna. W szczególnym przypadku może wystąpić jeden podwójny biegun dla którego charakterystyka zagnie się o 40 db/dek na dół. Będzie to zależało od wartości elementów. Warto więc sprawdzić jak wygląda charakterystyka naszego fizycznego układu.
Obliczenia układu
Dla podanych wcześniej wartości elementów policzmy najpierw stałe czasowe:

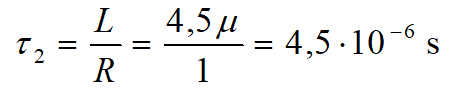
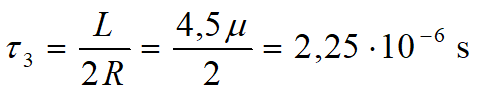 Częstotliwość zera charakterystyki amplitudowej jest równa:
Częstotliwość zera charakterystyki amplitudowej jest równa:
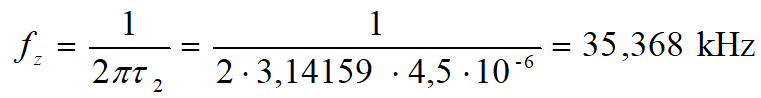 Do obliczenia częstotliwości biegunów trzeba rozwiązać równanie kwadratowe występujące w mianowniku transmitancji.
Do obliczenia częstotliwości biegunów trzeba rozwiązać równanie kwadratowe występujące w mianowniku transmitancji.
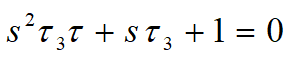
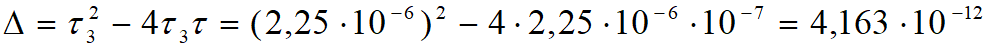
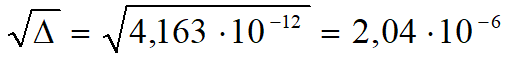
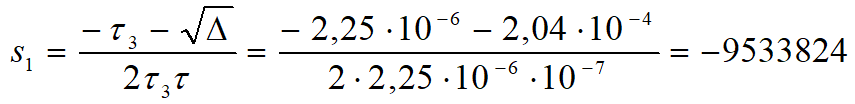
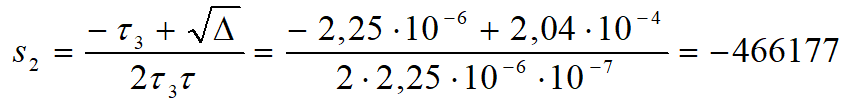 Częstotliwości biegunów są równe
Częstotliwości biegunów są równe
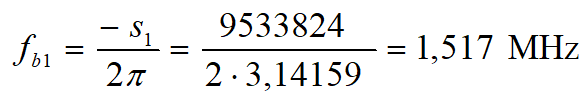
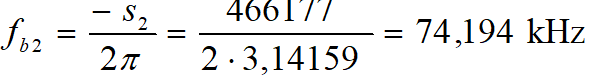 Mamy już wszystko co jest potrzebne do naszkicowania charakterystyki amplitudowej. Wiemy, że zaczyna się ona od poziomu –6 dB i przebiega ze stałą wartością do najniższej częstotliwości charakterystycznej transmitancji. Jest nią częstotliwość zera równa 35,368 kHz. Od tego punktu charakterystyka zaczyna się wznosić z szybkością 20 dB/dek aż do częstotliwości pierwszego bieguna, czyli do 74,194 kHz. Tu następuje załamanie charakterystyki w dół, czyli zaczyna ponownie przebiegać poziomo. Dla częstotliwości drugiego bieguna (1,517 MHz) następuje kolejne załamanie w dół, więc charakterystyka zaczyna opadać z szybkością 20 db/dek. Zanim zweryfikujemy obliczenia w symulatorze LTspice, naszkicujmy charakterystykę amplitudową naszej piramidy. Jej asymptotyczną postać przedstawiono na rysunku 5.
Mamy już wszystko co jest potrzebne do naszkicowania charakterystyki amplitudowej. Wiemy, że zaczyna się ona od poziomu –6 dB i przebiega ze stałą wartością do najniższej częstotliwości charakterystycznej transmitancji. Jest nią częstotliwość zera równa 35,368 kHz. Od tego punktu charakterystyka zaczyna się wznosić z szybkością 20 dB/dek aż do częstotliwości pierwszego bieguna, czyli do 74,194 kHz. Tu następuje załamanie charakterystyki w dół, czyli zaczyna ponownie przebiegać poziomo. Dla częstotliwości drugiego bieguna (1,517 MHz) następuje kolejne załamanie w dół, więc charakterystyka zaczyna opadać z szybkością 20 db/dek. Zanim zweryfikujemy obliczenia w symulatorze LTspice, naszkicujmy charakterystykę amplitudową naszej piramidy. Jej asymptotyczną postać przedstawiono na rysunku 5.
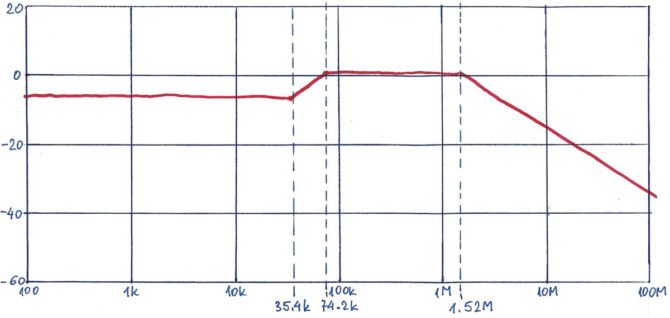 Rysunek 5. Odręczna charakterystyka amplitudowa badanego układu
Rysunek 5. Odręczna charakterystyka amplitudowa badanego układu
Weryfikacja obliczeń w symulatorze LTspice
Nadeszła chwila prawdy. Sprawdzimy czy obliczenia były prawidłowe. Emocje rosną…
Zaczniemy od bezpośredniej symulacji polegającej na narysowaniu w edytorze LTspice’a schematu piramidy, określeniu parametrów elementów i parametrów symulacji. Przestrzenna piramida została oczywiście rozłożona na płaszczyźnie (rysunek 6), jej schemat jest więc taki sam, jakiego używaliśmy do obliczeń (rysunek 4).
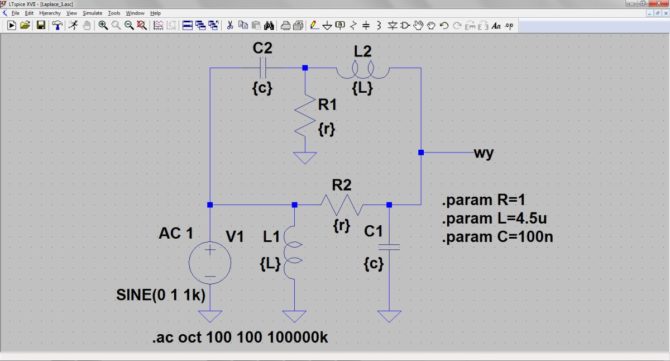 Rysunek 6. Schemat piramidy narysowany w edytorze LTspice’a
Rysunek 6. Schemat piramidy narysowany w edytorze LTspice’a
Wartości elementów określono parametrycznie, tak aby w razie konieczności można je było łatwo modyfikować. Do wejścia dołączamy źródło sygnału sinusoidalnego. Pamiętamy, że do analizy częstotliwościowej, którą przeprowadzimy konieczne jest określenie parametru AC=1. Symulację uruchamiamy komendą: .ac oct 100 100 100000k, rozpatrujemy więc zakres od 100 Hz do 100 MHz, analizujemy 100 punktów na oktawę. Wskazujemy wyprowadzenie „wy” jako punkt, do którego ma się odnosić wykres. Po chwili ukazuje się gotowa charakterystyka amplitudowa i fazowa. Tę ostatnią wyłączamy (rysunek 7).
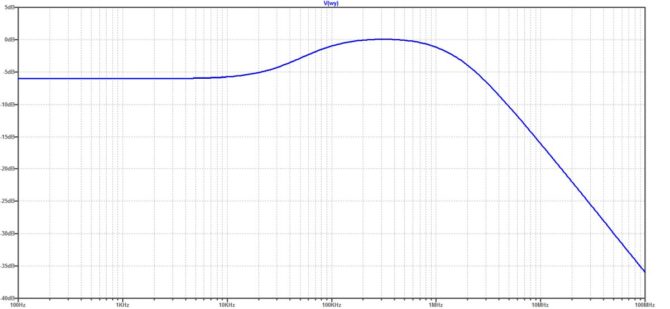 Rysunek 7. Charakterystyka amplitudowa uzyskana w wyniku symulacji w programie LTspice
Rysunek 7. Charakterystyka amplitudowa uzyskana w wyniku symulacji w programie LTspice
Choć w pierwszej chwili może wydawać się, że charakterystyki przewidywana i uzyskana w symulacji nie są jednakowe, to jednak po nałożeniu jednej na drugą okazuje się, że są one poprawne. Różnice wynikają z przyjęcia charakterystyki asymptotycznej dla wykresu odręcznego (rysunek 8). Ponadto bliskość zer i biegunów transmitancji powoduje, że rzeczywista charakterystyka nie zawsze nadąża za asymptotą. Jest to dość dobrze widoczne na odcinku pomiędzy 100 kHz a 1 MHz, w którym wykres asymptotyczny wyraźnie przekracza poziom 0 dB, a rzeczywisty tylko nieznacznie, niemal niezauważenie.
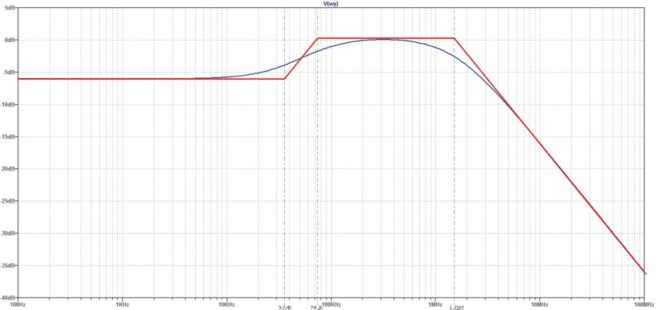 Rysunek 8. Porównanie odręcznej charakterystyk asymptotycznej i dokładnej uzyskanej w symulacji
Rysunek 8. Porównanie odręcznej charakterystyk asymptotycznej i dokładnej uzyskanej w symulacji
Przekształcenie Laplace’a
Przeprowadzona symulacja potwierdziła, że nasze obliczenia transmitancji były poprawne. Gdyby tak nie było, odręczny wykres sporządzony na jej podstawie różniłby się od wykresu uzyskanego z symulacji. Wyznaczenie zer i biegunów transmitancji pozwala szybko i względnie prosto z grubsza oszacować przebieg charakterystyk częstotliwościowych rozpatrywanego układu. Na wykresach asymptotycznych nie są jednak widoczne łagodne załamania charakterystyk w okolicach zer i biegunów. Nie są też dokładnie widoczne wzajemne oddziaływania sąsiadujących ze sobą zer i biegunów. Aby wykreślić dokładną charakterystykę częstotliwościową należy punkt po punkcie przeliczyć odpowiedź układu na pobudzenie sygnałem sinusoidalnym. Transmitancja jest – można powiedzieć – matematycznym opisem rozpatrywanego układu elektronicznego, i dlatego może być używana do badania odpowiedzi dowolnego układu na dowolny sygnał wymuszający, nawet bardzo złożony.
Do badania zachowywania się układów zawierających elementy reaktancyjne (indukcyjności, pojemności) konieczne są obliczenia liniowych równań różniczkowych zwyczajnych, co w szczególnych przypadkach wymaga wiedzy z zakresu matematyki wyższej i nie są to zadania łatwe. Rozwiązywanie takich zagadnień może być znacznie uproszczone przez zastosowanie transformaty Laplace’a przekształcającej równanie różniczkowe w równanie algebraiczne zawierające operator Laplace’a s. Skorzystaliśmy z tej metody obliczając transmitancję, a teraz pozostaje tylko obliczenie odpowiedzi układu na wymuszenie.
Transformata Laplace’a w LTspice
Już sama terminologia matematyczna może budzić strach i przerażenie, ale diabeł nie jest taki straszny jak go malują. Nie będziemy na piechotę liczyć żadnych transformat czy rozwiązywać równań różniczkowych, zrobi to za nas symulator LTspice. Konieczne będzie jedynie przerysowanie schematu naszej piramidy do takiej postaci, która umożliwi zastosowanie standardowej funkcji matematycznej programu LTspice o nazwie Laplace. Aby móc porównać wyniki rozbudujemy schemat z rysunku 6 o źródło napięciowe sterowane napięciowo (rysunek 9). Jest ono oznaczone w bibliotece LTspice’a literką E. We właściwościach tego źródła, w polu „Value” wpisujemy wyrażenie odpowiadające transmitancji układu, a więc:
Laplace=1/2*(s*t2+1)/(s*s*t3*t1+s*t3+1)
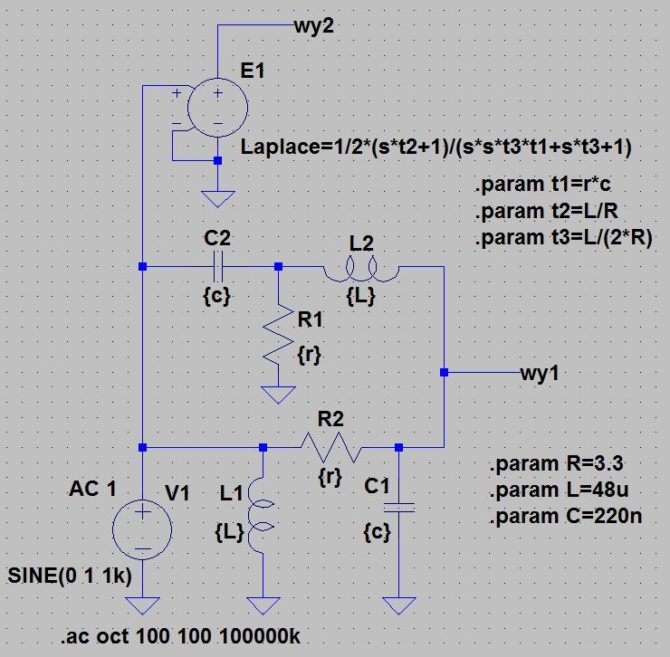 Rysunek 9. Przygotowanie symulacji z zastosowaniem przekształcenia Laplace’a
Rysunek 9. Przygotowanie symulacji z zastosowaniem przekształcenia Laplace’a
Jak widać, występuje w nim operator Laplace’a s oraz parametry t1, t2 i t3. Są to stałe czasowe odpowiednio τ, τ1 i τ2 z wcześniejszych obliczeń. Wejście sterujące „-” tego źródła jest dołączone do masy, a wejście „+” dołączamy do źródła sygnału wejściowego. Jak widać, do symulacji układu o znanej transmitancji nie są już potrzebne żadne dodatkowe elementy. Uruchamiamy więc symulację AC Analysis i wskazujemy wyjście „wy2”. Na ekranie ukazuje się wykres do złudzenia przypominający ten z poprzedniej symulacji. I w tym przypadku rozpatrujemy wyłączenie charakterystykę napięciową, fazową więc wyłączamy. Aby jednak mieć stuprocentową pewność, że wykresy są identyczne klikamy na wyjście „wy1”, dołączając tym samym przebieg wyjściowy naszej piramidy do wyniku końcowego. Wykresy idealnie nałożyły się na siebie, więc teraz już jesteśmy pewni, że obliczona transmitancja jest poprawna.
Sprawdzenie odpowiedzi na różne wymuszenia
Zgodnie z tym co już było powiedziane, znajomość transmitancji układu pozwala badać jego odpowiedź na różne wymuszenia, nie tylko sinusoidalne. Zobaczmy więc, jak nasza piramida odpowie na przykład na impuls prostokątny o amplitudzie 1 V, czasie narastania 10 μs, czasie trwania 30 μs, czasie opadania 20 μs i okresie powtarzania 150 μs? W tym celu definiujemy źródło napięcia wejściowego:
PULSE(0 1 0 10u 20u 30u 150u)
i uruchamiamy symulację TRAN 300u. Wyniki przedstawiono na rysunku 10.
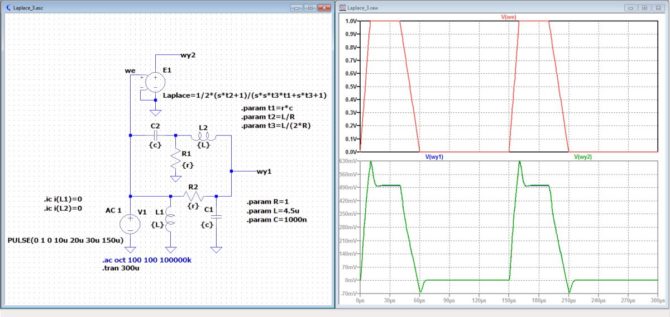 Rysunek 10. Odpowiedź układu na pobudzenie impulsowe
Rysunek 10. Odpowiedź układu na pobudzenie impulsowe
Na dolnym wykresie nałożono sygnały z wyjścia „wy1” i „wy2”. I w tym przypadku są one identyczne. W symulacji zastosowano dodatkową komendę zapewniającą zerowy prąd w obu indukcyjnościach w chwili początkowej. Są to polecenia:
.ic i(L1)=0
.ic i(L2)=0
Weryfikacja pomiarowa
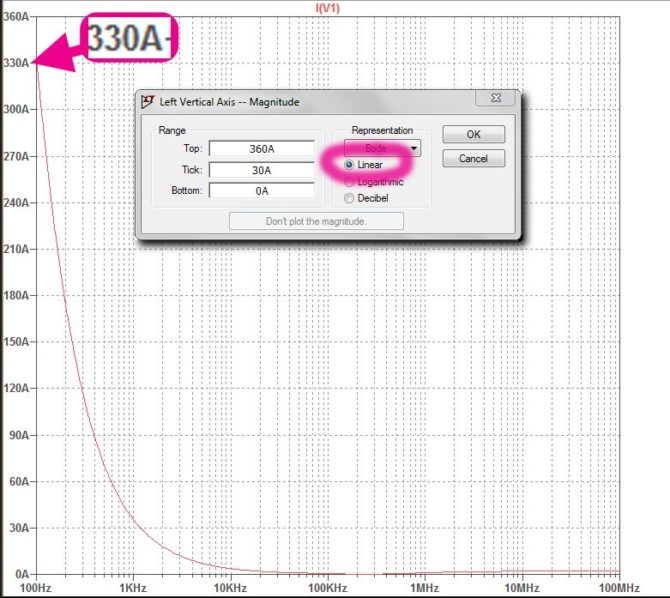
Tu niestety czeka nas przykra niespodzianka. Weryfikacji pomiarowej tym razem nie będzie. Dlaczego? Sprawdźmy, jaki będzie prąd pobierany ze źródła wejściowego w symulacji AC Analysis? Powracamy do schematu pomiarowego z rysunku 10, z tym że zamiast na wyjście klikamy na źródło V1. Uzyskujemy tym samym charakterystykę poboru prądu w funkcji częstotliwości, ale nie interesują nas zmiany względne, tylko wartości bezwzględne. Dlatego zmieniamy skalę pionową wykresu klikając na nią, a następnie wybierając opcję „Linear” (rysunek 11).
 Rysunek 11. Symulowany pomiar prądu pobieranego ze źródła wymuszającego
Rysunek 11. Symulowany pomiar prądu pobieranego ze źródła wymuszającego
Wszystko staje się jasne. Dla niskich częstotliwości prąd pobierany ze źródła V1 musiałby mieć natężenie rzędu dziesiątek, a nawet setek amperów (maksimum 330 A). To oczywiście wymagania przekraczające możliwości Analog Discovery 2. No cóż. Musimy się z tym pogodzić, ważne jest natomiast, że mamy świadomość, dlaczego pomiar jest niemożliwy.
Zagrożenia przy symulacjach z użyciem transmitancji
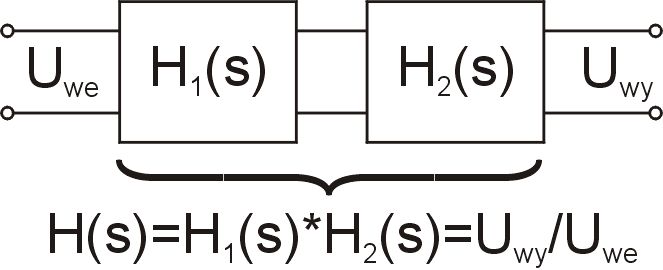
Pojęcie transmitancji jest dość szerokie. W zależności od metod analizy układu, nie tylko zresztą elektronicznego, można wyróżnić np. transmitancję operatorową czy widmową. Nie wdając się w szczegóły przyjmijmy, że jest to funkcja opisująca zależność sygnału wyjściowego od wejściowego. Dysponując kilkoma czwórnikami o znanych transmitancjach można obliczyć np. wypadkową transmitancję kaskadowego ich połączenia, co jest częstym przypadkiem spotykanym w praktyce (rysunek 12).
 Rysunek 12. Transmitancja wypadkowa połączenia kaskadowego czwórników
Rysunek 12. Transmitancja wypadkowa połączenia kaskadowego czwórników
Jest ona równa iloczynowi transmitancji poszczególnych czwórników. Dla układu z rysunku 12 transmitancja wypadkowa będzie równa H(s)=H1(s)*H2(s). Ale uwaga: transmitancja każdego czwórnika jest liczona przy założeniu, że nie jest on niczym obciążony. W układzie z rysunku 12 oznacza to, że oporność wejściowa czwórnika o transmitancji H2(s) musi być wielokrotnie wyższa niż oporność wyjściowa poprzedzającego czwórnika H1(s).
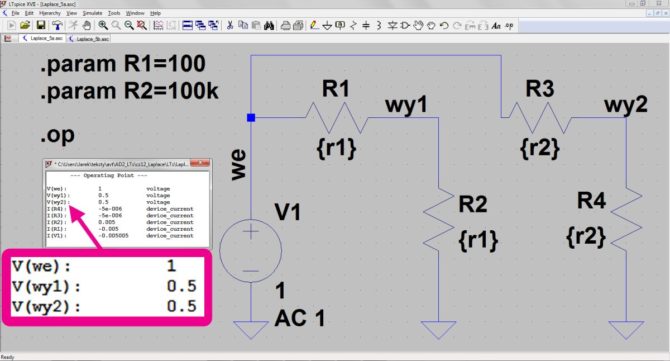
Sprawdźmy to dla przykładu czwórników tworzących rezystorowe dzielniki napięciowe. Pierwszy składa się z rezystorów 100 Ω drugi ma rezystory 100 kΩ (rysunek 13). Transmitancje tych czwórników są równe:
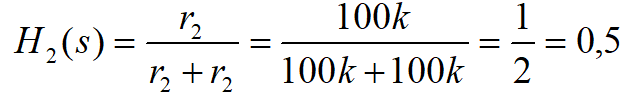
 Rysunek 13. Wyznaczenie transmitancji dwóch czwórników – dzielników rezystorowych
Rysunek 13. Wyznaczenie transmitancji dwóch czwórników – dzielników rezystorowych
Przy połączeniu kaskadowym czwórników transmitancja powinna być równa H(s)=0,5*0,5=0,25. Sprawdźmy to dołączając czwórnik z rezystorami r2=100 kΩ do czwórnika z rezystorami r1=100 Ω (rysunek 14a), a następnie zamieniając kolejność czwórników (rysunek 14b). W pierwszym przypadku rzeczywiście uzyskaliśmy wynik bliski 0,25 – dokładnie 0,249938, ale w drugim napięcie wyjściowe stanowi zaledwie 0,000996016 napięcia wejściowego (sic!). Na takie detale warto zwracać uwagę podczas analizy układów elektronicznych, gdyż uzyskiwane wyniki mogą czasami wprowadzać nas w zakłopotanie.







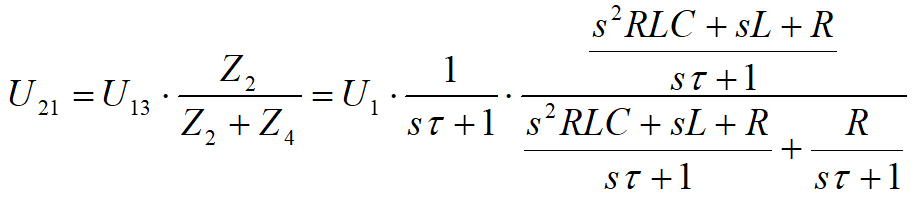

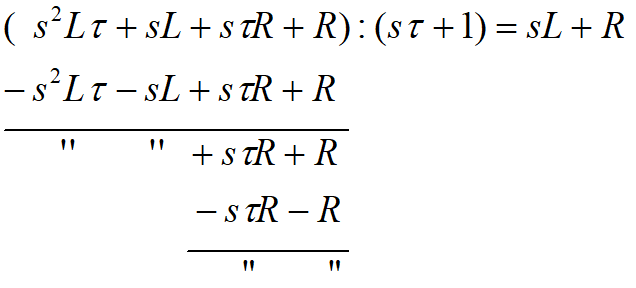
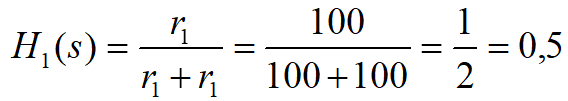
 Czy potężny rozbłysk słoneczny zagraża Ziemi? [opinia eksperta IŁ]
Czy potężny rozbłysk słoneczny zagraża Ziemi? [opinia eksperta IŁ]  Świetlana przyszłość przemysłu elektronicznego według Dave Doherty, prezesa zarządu DigiKey
Świetlana przyszłość przemysłu elektronicznego według Dave Doherty, prezesa zarządu DigiKey 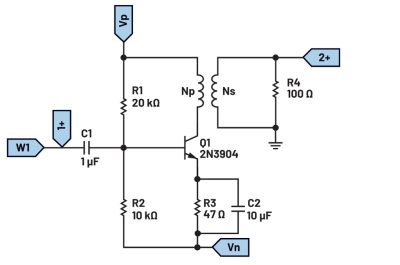 Zastosowanie zestawu ADALM2000 do pomiarów wzmacniacza sprzężonego transformatorowo
Zastosowanie zestawu ADALM2000 do pomiarów wzmacniacza sprzężonego transformatorowo