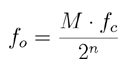Struktura DDS

Nakładem Wydawnictwa BTC ukazała się książka „Syntezery DDS. Podstawy dla konstruktorów”, w której autor przedstawił najpopularniejsze scalone układy DDS oraz przykłady ich aplikacji. O książce Metoda bezpośredniej syntezy cyfrowej DDS (Direct Digital Synthesis) to nowoczesna technika generacji sygnałów, całkowicie oparta na technice cyfrowej. Pozwala na łatwe i precyzyjne modyfikowanie parametrów generowanych sygnałów, a dzięki nowatorskim rozwiązaniom wymaga stosowania coraz mniejszej liczby elementów dyskretnych, coraz prostsze są także tory analogowe współpracujące ze scalonymi syntezerami. W książce przedstawiono elementarne podstawy teoretyczne cyfrowej syntezy sygnałów, dostępne na rynku scalone generatory DDS, ich możliwości, sposób sterowania, przedstawiono także przykładowe projekty kompletnych, sprawdzonych przez autora, rozwiązań. Książka jest przeznaczona dla elektroników-praktyków, którzy chcą poznać….

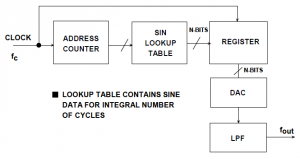
Wraz z upowszechnieniem wykorzystania techniki cyfrowej w oprzyrządowaniu i systemach komunikacji, sterowana cyfrowo metoda generowania wielu częstotliwości w oparciu o częstotliwość referencyjną wyewoluowała w technikę zwaną bezpośrednią syntezą cyfrową (DDS). Podstawowa struktura została pokazana na rysunku 1.

Rys. 1. Podstawowy schemat blokowy systemu bezpośredniej syntezy cyfrowej

W tym uproszczonym modelu stabilny zegar steruje programowalną pamięcią PROM, która przechowuje jeden lub więcej cykli sinusoid (lub innego ustalonego wcześniej przebiegu). W miarę, jak licznik adresów przechodzi przez kolejne komórki pamięci, odpowiadająca każdej komórce amplituda cyfrowa steruje przetwornikiem cyfrowo-analogowym (DAC), który z kolei generuje analogowy sygnał wyjściowy. Czystość widma ostatecznego sygnału analogowego na wyjściu zależy głównie od przetwornika. Szum fazowy jest praktycznie taki, jak w zegarze referencyjnym.

Ponieważ system DDS jest systemem opartym na danych spróbkowanych, wszystkie kwestie związane z próbkowaniem muszą zostać rozważone: szum kwantyzacji, aliasing, filtrowanie itp. Na przykład harmoniczne wyższych rzędów na wyjściu DAC wchodzą w skład widma w paśmie Nyquista, co sprawia, że nie mogą zostać odfiltrowane. Jednocześnie harmoniczne wyższych rzędów na wyjściu syntezatorów opartych o PLL mogą być filtrowane. Istnieją również inne problemy, które zostaną omówione dalej.

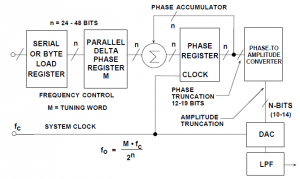
Podstawowym problemem w prostym systemie DDS jest fakt, że końcowa częstotliwość na wyjściu może być zmieniona jedynie poprzez zmianę częstotliwości zegara odniesienia lub przeprogramowanie pamięci PROM, co jest raczej niewygodne. W praktycznym systemie DDS podstawowa funkcja została zaimplementowana w znacznie bardziej efektywny sposób, przy użyciu oscylatora kontrolowanego numerycznie (NMO). Schemat blokowy takiego systemu został pokazany na rysunku 2.

Rys. 2. Elastyczny system DDS

Serce systemu stanowi akumulator fazy (phase accumulator), którego zawartość jest uaktualniania w każdym cyklu zegara. Za każdym razem, gdy akumulator fazy jest aktualizowany, liczba całkowita M przechowywana w rejestrze zmiany fazy (delta phase register) jest dodawana do wartości w rejestrze akumulatora fazy. Przypuśćmy, że liczba w rejestrze zmiany fazy ma postać 00…01, a początkowa zawartość akumulatora fazy to 00…00. Akumulator fazy jest zwiększany o 00…01 w każdym cyklu zegara. Jeśli akumulator ma długość 32 bitów, potrzeba 2^32 (ponad 4 miliardów) cykli zegara, zanim akumulator fazy powróci do stanu 00…00 i cykl rozpocznie się od nowa.

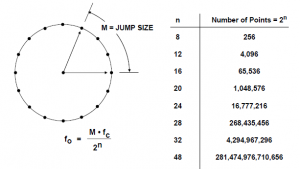
Obcięta wartość akumulatora fazy służy do adresowania tablicy wartości sinusa (lub cosinusa). Każdy adres w tej tablicy odpowiada wartości fazy sinusoidy od 0? do 360?. Tablica wartości określa amplitudę sygnału cyfrowego dla całego okresu sinusoidy (w rzeczywistości tylko dane do 90? są potrzebne, ponieważ informacje o aktualnej ćwiartce są przechowywane na dwóch najstarszych bitach). Tablica wartości w rzeczywistości mapuje informacje o fazie z akumulatora fazy na wartości amplitudy cyfrowej, która wysterowuje przetwornik. Graficznie pokazuje to „okrąg fazy” na rysunku 3.

Rys. 3. Okrąg fazy cyfrowej

Załóżmy n = 32 oraz M = 1. Akumulator fazy przechodzi przez każde 2^32 możliwe stany, zanim się przepełni i wróci do początku. Odpowiadająca temu częstotliwość sinusoidy jest równa częstotliwości zegara dzielonej przez 2^32. Gdy M = 1, rejestr akumulatora fazy przepełnia się dwa razy szybciej, a uzyskana częstotliwość ulega podwojeniu. Można to uogólnić w następujący sposób:

Dla n-bitowego akumulatora fazy (n z reguły waha się od 24 do 32 w większości systemów DDS) istnieją 2^n możliwe wartości fazy. Wartość rejestru przesunięcia fazy M oznacza liczbę, o którą akumulator fazy jest zwiększany w każdym cyklu zegara. Jeśli fc oznacza taktowanie zegara, to częstotliwość wyjściowej sinusoidy jest równa:

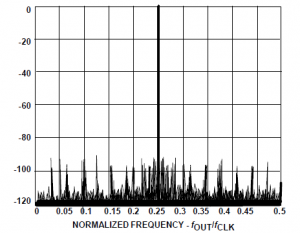
To równanie jest znane jako „równanie strojenia” DDS (tuning equation). Warto zauważyć, że rozdzielczość częstotliwościowa systemu jest równa fc/2^n. Dla n = 32, rozdzielczość jest wyższa, niż jedna część na cztery miliardy. W rzeczywistym systemie DDS wszystkie bity akumulatora fazy nie są przesyłane do tablicy wartości, lecz przycinane, pozostawiając tylko 13 do 15 najstarszych bitów. Pozwala to zmniejszyć rozmiar tablicy wartości, lecz nie powoduje utraty rozdzielczości częstotliwościowej. Obcinanie fazy wnosi jedynie niewielki, akceptowalny szum fazowy do generowanego sygnału (rysunek 4).

Rys. 4. Obliczone widmo sygnału wejściowego pokazuje zakres dynamiczny – różnicę między generowaną częstotliwością a szumami (SFDR) równy 90 dB przy obcięciu fazy do 15 bitów