Biblioteka DSP dla mikrokontrolerów LPC1700 i LPC1300 firmy NXP
Wydajność obliczeń filtru przedstawiono w tabeli 9.
Tab. 9. Filtr FIR
| Mnożnik zegara pamięci 1 | Mnożnik zegara pamięci 2 | Mnożnik zegara pamięci 3 | ||||
| (20 MHz maks.) | (40 MHz maks.) | (60 MHz maks.) | ||||
| Cykle | Czas (μs) | Cykle | Czas (μs) | Cykle | Czas (μs) | |
| 32 próbki i współczynniki | 3433 | 171,650 | 3455 | 86,125 | 3470 | 57,833 |
| Mnożnik zegara pamięci 4 | Mnożnik zegara pamięci 5 | Mnożnik zegara pamięci 6 | ||||
| (80 MHz maks.) | (100 MHz maks.) | (120 MHz maks.) | ||||
| Cykle | Czas (μs) | Cykle | Czas (μs) | Cykle | Czas (μs) | |
| 32 próbki i współczynniki | 3495 | 43,688 | 3520 | 35,200 | 3520 | 29,333 |
Rezonator (oscylator)
Funkcja rezonatora jest bardzo ekonomicznym sposobem generowania sygnału sinusoidalnego – bez potrzeby korzystania z tablic lub przybliżeń funkcji trygonometrycznych. Co istotne, algorytm ten jest jedynie specjalnym przypadkiem wykorzystania sekcji bikwadratowej, jednak ze współczynnikami licznika równymi zero i dwoma biegunami leżącymi na okręgu jednostkowym, dzięki czemu układ oscyluje.
Wzór opisujący rezonator za pomocą funkcji czasu dyskretnego:
Reprezentacja w dziedzinie zmiennej zespolonej Z:
Odwoływanie się do rezonatora:
typedef struct
{
int i_C oeff_a1;
int i_yn_1;
int i_yn_2;
}tS_ResonatorStateCoeff;
void vF_dspl_resonator(int *psi_Output, void *pS_ResonatorStateCoeff, int i_NSamples);
Ponieważ algorytm rezonatora jest rekurencyjny, należy zwrócić szczególną uwagę na skalowanie parametrów. Współczynniki i stan rezonatora należy ustawić następująco:
i_Coeff_a1 = 2.0 * cos(Omega) * pow(2.0,14)
By rozpocząć oscylacje, należy ustawić następujący stan początkowy:
i_yn_1 = 0;
i_yn_2 = -Amplitude * sin(Omega) * pow(2.0,14)
gdzie:
Omega – częstotliwość jako ułamek częstotliwości próbkowania
Amplitude – zadana amplituda sygnału. Musi być mniejsza od 2,0 z powodu stosowania arytmetyki '2.14′.
Format liczbowy '2.14′ został użyty, ponieważ współczynnik a1 jest większy, niż 1, a pojedynczy cykl mnożenia gwarantuje brak przepełnienia tylko, jeśli mnożnik i mnożna są 16-bitowe.
Wydajność obliczeń przedstawiono w tabeli 10.
Tab. 10. Rezonator
| Mnożnik zegara pamięci 1 | Mnożnik zegara pamięci 2 | Mnożnik zegara pamięci 3 | ||||
| Rezonator | (20 MHz maks.) | (40 MHz maks.) | (60 MHz maks.) | |||
| Cykle | Czas (μs) | Cykle | Czas (μs) | Cykle | Czas (μs) | |
| 512 próbek | 5153 | 257,650 | 5157 | 128,925 | 5161 | 86,017 |
| Mnożnik zegara pamięci 4 | Mnożnik zegara pamięci 5 | Mnożnik zegara pamięci 6 | ||||
| Rezonator | (80 MHz maks.) | (100 MHz maks.) | (120 MHz maks.) | |||
| Cykle | Czas (μs) | Cykle | Czas (μs) | Cykle | Czas (μs) | |
| 512 próbek | 5166 | 64,575 | 5172 | 51,720 | 5172 | 43,100 |
Kontrola PID
Algorytm PID (’ Proportional, Integral, Differential ’) jest powszechnie wykorzystywany, gdyż zapewnia bardzo umiarkowane zużycie procesora.
Równanie czasu dyskretnego PID:
Wywoływanie funkcji kontroli PID:
typedef struct
{
short int Kp;
short int Ki;
short int Kd;
short int IntegratedError;
short int LastError;
}tS_pid_Coeff;
short int vF_dspl_pid(short int si_Error, tS_pid_Coeff *pS_Coeff);






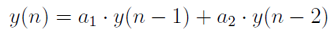
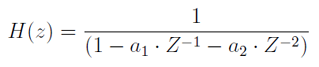

 Caroline Pannier – nowa dyrektorka targów electronica – analizuje sytuację gospodarczą branży i przedstawia wyniki
Caroline Pannier – nowa dyrektorka targów electronica – analizuje sytuację gospodarczą branży i przedstawia wyniki  Konstrukcja Ventiva Zoned Cooling™ – ukierunkowane chłodzenie powietrza dla urządzeń AI Edge
Konstrukcja Ventiva Zoned Cooling™ – ukierunkowane chłodzenie powietrza dla urządzeń AI Edge  Komunikacja dalekiego zasięgu oparta na technologii Qualcomm dla robotyki i dronów
Komunikacja dalekiego zasięgu oparta na technologii Qualcomm dla robotyki i dronów 






