Poradnik LTspice tips&tricks #5 – symulacja metodą Monte Carlo i Worst Case
„Inżynierska dokładność” to termin, z którym inżynierowie-elektronicy spotykają się na co dzień. Jakże często okazuje się, że nie ma co kruszyć kopii o precyzję obliczeń elementów elektronicznych – przecież i tak w praktyce stosowane są elementy z szeregu, a nie takie, które wynikają z obliczeń. Czy zawsze możemy sobie pozwolić na taką dowolność?
W roboczym magazynku, który wykorzystuję na co dzień do prac prototypowych mam rezystory i kondensatory o zaledwie kilku wartościach z szeregu. Okazuje się, że dużą część projektów udaje się zrealizować z ich użyciem i rzadko magazynek muszę powiększać o elementy, których w nim nie było. Nie jest to oczywiście reguła. Są projekty, które jednak wymagają precyzyjnych wartości elementów, a stosując typowe, zgadzamy się na pogorszenie parametrów całego urządzenia. Solidny inżynier decydując się na któryś z tych wariantów powinien, przynajmniej teoretycznie, ocenić skutki podjętej decyzji. W eksperymencie, który przeprowadzimy, dokładny dobór wartości elementów ma bardzo istotne znaczenie. Spróbujemy więc zbadać, na jaki „luz” można sobie pozwolić w podobnym projekcie.
Są na niej weryfikowane przykłady przedstawione w cyklu artykułów i na filmach. Liczba zestawów Analog Training Board (ATB) dostępnych w cenie promocyjnej jest ograniczona.
Projekt mostka typu „podwójne T”
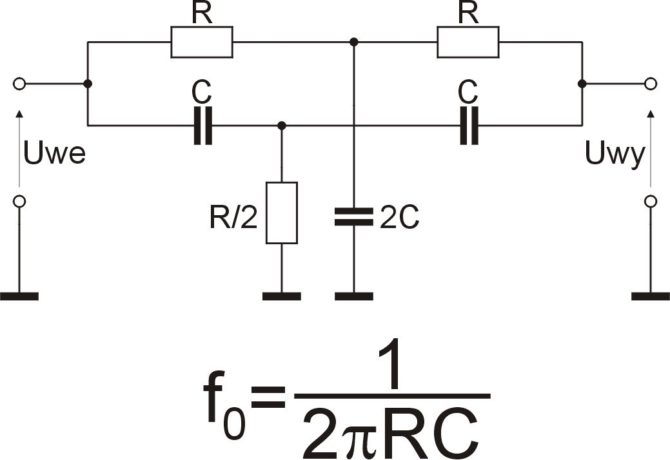
Załóżmy, że w jakimś urządzeniu musimy selektywnie wyciąć sygnał o określonej częstotliwości. Niech to będzie dla ustalenia uwagi 3700 Hz. Bardzo dobrym rozwiązaniem jest w takich przypadkach mostek TT charakteryzujący się bardzo dobrą selektywnością (rys. 1). Jest to filtr środkowo-zaporowy o częstotliwości środkowej określonej wyrażeniem:
Jeżeli przyjmiemy pojemność kondensatora C równą 10 nF, to z obliczenia wynika, że rezystancja R powinna być równa 4301 Ω. Zakładamy, że filtr powinien być zaprojektowany z jak największą dokładnością. Wybieramy więc najbliższą wartość z szeregu 1-procentowego, to znaczy 4320 Ω. Musimy zatem zgodzić się na to, że częstotliwość filtru nieco się zmieni. Po przeliczeniu okazuje się, ze będzie ona równa 3684 Hz. Różnica jest równa 16 Hz, co stanowi 0,43% wartości zakładanej. Gdyby chodziło o sygnał akustyczny, to różnicę między dźwiękami o częstotliwościach 3684 Hz i 3700 Hz byłyby w stanie wykryć nawet osoby bez słuchu absolutnego, ale raczej tylko wtedy, gdyby je odsłuchiwały bezpośrednio, jeden po drugim. Przyjmijmy jednak, że nie chodzi o zastosowania akustyczne i taka niedokładność nas zadowala.
No dobrze, ale to obliczenie dotyczy przypadku, w którym wszystkie elementy mostka mają wartości znamionowe. W rzeczywistości każdy z nich zmienia się losowo w granicach ±1% wokół wartości znamionowej. W sposób nieunikniony spowoduje to zmianę częstotliwości środkowej każdej realizacji praktycznej filtru. Mamy więc sporo elementów, a każdy z nich zmienia się losowo. Czy jest jakaś metoda, aby to wszystko jakoś ogarnąć?
Artykuł jest częścią pełnego kursu obsługi symulatora układów elektronicznych LTspice pt. „LTspice tips&tricks”. Kurs składa się z 10 części:
- Jak używać w symulacjach sygnałów zewnętrznych oraz jak w układach rzeczywistych korzystać z sygnałów wytwarzanych przez symulator
- Pomiary wzmacniacza standardowego i rail-to-rail
- Strojone filtry dolno- i górnoprzepustowe
- Pomiary harmonicznych
- Symulacja metodą Monte Carlo i Worst Case – czytasz ten artykuł
- Scrambler audio: odwracanie widma i kilka innych tricków
- Tajniki próbkowania (aliasing) sygnałów analogowych
- Wzmacniacze pomiarowe,
- Wzmacniacz tranzystorowy w układzie ze wspólnym emiterem (OE)
- LTspice jako narzędzie przydatne w obliczeniach transmitancji
Każdy odcinek ukazał się także w wersji wideo. Materiały te dostępne są na portalu YouTube
Monte Carlo to nie tylko słynne kasyno
Okazuje się, że metoda taka istnieje. Co więcej, w dwuosobowym zespole, który ją opracował był nasz rodak Stanisław Marcin Ulam. Drugim autorem był Węgier John von Neumann i obaj brali udział m.in. w pracach nad amerykańską bombą termojądrową. Już w roku 1949 opracowali oni metodę pozwalającą symulować różne zjawiska losowe. Dzisiaj, w epoce powszechnie używanych komputerów, metoda Monte Carlo jest wykorzystywana w bardziej pokojowych projektach, np. w modelowaniu zjawisk pogodowych, finansowych, w różnego rodzaju programach symulacyjnych itp. Funkcję mc używaną w symulacjach metodą Monte Carlo zaimplementowano m.in. w programie LTspice. Ma ona składnię:
mc (nom,tol)
Nom to wartość nominalna jakiegoś parametru, a tol określa jego tolerancję. Podczas symulacji generowana jest losowa wartość parametru, która jest następnie brana do dalszych obliczeń. Zawiera się ona w zakresie od nom-tol*nom do nom+tol*nom. Przykładowo, jeśli chcemy użyć tej funkcji do określenia rezystancji rezystora naszego mostka TT, to zamiast podawania jego rezystancji znamionowej musimy użyć formuły {mc(4320, 0.01)} – rezystancja znamionowa 4320 Ω, tolerancja 1%.
Mostek TT składa się zasadniczo z 3 rezystorów i 3 kondensatorów. Wartości elementów należących do pionowych gałęzi są równe 2C i R/2. W realizacji praktycznej można szukać pojedynczych elementów spełniających te zależności, ale nie zawsze jest to możliwe. Na przykład rezystor R/2 naszego mostka musiałby mieć rezystancję 2160 Ω, a takiego nie ma w szeregu nawet 1-procentowym. Innym rozwiązaniem jest użycie dwóch elementów połączonych równolegle. Dwa rezystory R połączone równolegle dadzą rezystancję R/2, a tak samo połączone kondensatory C dadzą pojemność 2C. Musimy jednak pamiętać, że oporności i pojemności elementów wziętych do realizacji praktycznej będą się zmieniały losowo w zakresie trudnym do przewidzenia dla danego przypadku. Robi się prawdziwy galimatias, co sprawia, że trudno określić zakres zmian częstotliwości środowych rzeczywistych filtrów. I to jest powód, dla którego symulacja metodą Monte Carlo może dać w miarę sensowną odpowiedź.
Symulacja mostka TT z zastosowaniem bibliotecznej funkcji mc symulatora LTspice
Schemat mostka przygotowany w edytorze symulatora LTspice przedstawiono na rys. 2. Wartości znamionowe elementów R i C oraz ich tolerancje zostały określone parametrycznie poleceniami:
- Rezystancja – .param R=4320,
- Pojemność – .param C=10m,
- Tolerancja rezystancji- tolr=.01,
- Tolerancja pojemności – .param tolc=.01.
Wartości każdego elementu mostka określono natomiast za pośrednictwem funkcji mc:
- {mc(R,tolr)} dla rezystorów,
- {mc(C,tolc)} dla kondensatorów.
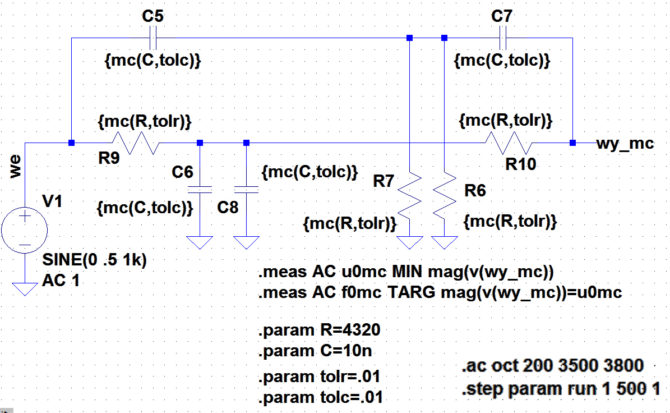 Rys. 2. Przygotowanie symulacji mostka TT z zastosowaniem funkcji mc
Rys. 2. Przygotowanie symulacji mostka TT z zastosowaniem funkcji mc
Zbadanie wpływu rozrzutu wartości elementów mostka wymaga wykonania wielu symulacji, tak aby można było wyciągnąć jakieś wnioski statystyczne. W symulatorze LTspice służy do tego celu komenda np. .step param run 1 500 1. Pojedyncze uruchomienie symulacji powoduje wykonanie w tym przypadku 500 wirtualnych sesji. W każdej z nich jest zmieniana zmienna RUN w zakresie od 1 do 500 z krokiem równym 1. W każdym przebiegu wykonywana jest symulacja częstotliwościowa AC, podczas której jest określana częstotliwość środkowa mostka. Służą do tego komendy:
.meas AC u0mc MIN mag(v(wy_mc))
.meas AC f0mc TARG mag(v(wy_mc))=u0mc
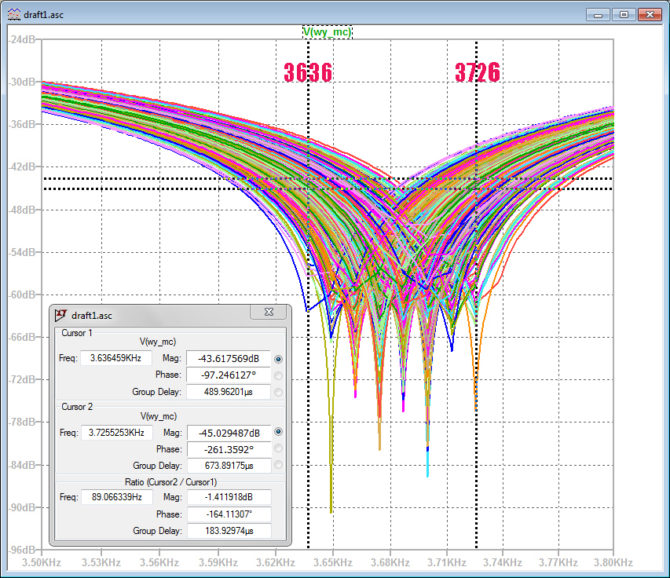
Pierwsza z nich wykrywa minimalny poziom sygnału wyjściowego i zapisuje go w zmiennej u0min. Druga komenda śledzi częstotliwość pomiarową aż do momentu, w którym poziom sygnału wyjściowego osiąga minimum. Śledzenie zostaje wówczas zakończone (opcja TARG), a w zmiennej f0mc zostaje zatrzaśnięta częstotliwość, która odpowiada częstotliwości środowej mostka. Dane te są dostępne po zakończeniu symulacji w logach błędów. Na ich podstawie określamy skrajne częstotliwości mostków. Z symulacji wynika, że dla użytych elementów możemy spodziewać się rozrzutu częstotliwości środkowych poszczególnych realizacji mostka w zakresie od 3636 Hz do 3726 Hz. Odetchnęliśmy z ulgą, gdyż obliczona częstotliwość środkowa zawiera się w tym przedziale.
Rozkład wartości generowanych przez funkcję
Jedna rzecz natomiast może niepokoić. Wprawdzie nie widać jej gołym okiem, ale warto zbadać, jaki jest rozkład wartości losowych generowanych funkcją mc? Dla sprawdzenia zmierzymy więc najpierw symulacyjnie np. pojemność kondensatora. Będzie to kondensator o pojemności znamionowej 10 nF i tolerancji 5%. Schemat pomiarowy przedstawiono na rys. 4. Pojemność kondensatora obliczymy na podstawie znajomości jego reaktancji. Do jej obliczenia będzie z kolei potrzebne wyznaczenie napięcia skutecznego na kondensatorze i prądu skutecznego przepływającego przez kondensator. Doprowadzimy do niego napięcie zmienne o częstotliwości 20 kHz. Potrzebne formuły są następujące:
- .meas Us RMS V(Uc) – obliczenie napięcia skutecznego na kondensatorze,
- .meas Ismc RMS I(C1) – obliczenie prądu skutecznego płynącego przez kondensator,
- .meas Xcmc param Us/Ismc – obliczenie reaktancji kondensatora,
- .meas Cznmc param 1/(2*pi*f*Xcmc) – obliczenie pojemności kondensatora.
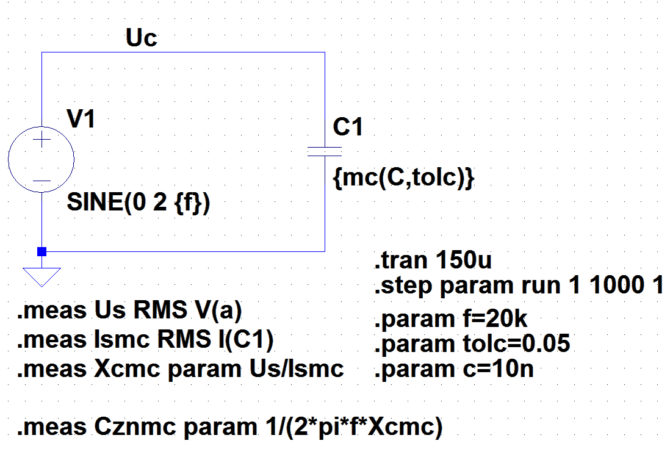 Rys. 4. Symulacyjny pomiar pojemności kondensatora funkcją mc
Rys. 4. Symulacyjny pomiar pojemności kondensatora funkcją mc
Pojemność kondensatora jest oczywiście określona za pomocą funkcji mc. Wykonamy pomiar 1000 wirtualnych kondensatorów (.step param run 1 1000 1).
Wyniki symulacji
Po zakończonej symulacji kopiujemy wyniki pojemności kondensatorów do pamięci podręcznej i wklejamy je do Excela. Pierwszą kolumnę można usunąć, gdyż jest to tylko liczba porządkowa. Drugą kolumnę wymnażamy natomiast przez 1000000000, aby wyeliminować mało czytelny zapis naukowy i uzyskać wyniki bezpośrednio w nanofaradach. W kolejnej kolumnie umieszczamy przyjęty arbitralnie zakres analizy: od 9,4 nF do 11 nF co 0,05 nF. Teraz można już wyznaczyć rozkład uzyskanych pojemności. Wykorzystujemy do tego excelową funkcję Histogram. Okazuje się, że symulacyjnie zmierzone pojemności mają rozkład przedstawiony na rys. 5. Na pewno nie jest to rozkład normalny, którego można by się spodziewać. Bardziej przypomina rozkład równomierny. Dla porównania na rys. 6 przedstawiono rozkład pojemności kondensatorów rzeczywistych o pojemności znamionowej 47 nF zmierzonych narzędziem „Impedance” zestawu Analog Discovery 2. Wprawdzie próba była znacznie mniej liczna (tylko 100 elementów), ale okazała się wystarczająca, aby uznać, że uzyskano rozkład normalny.
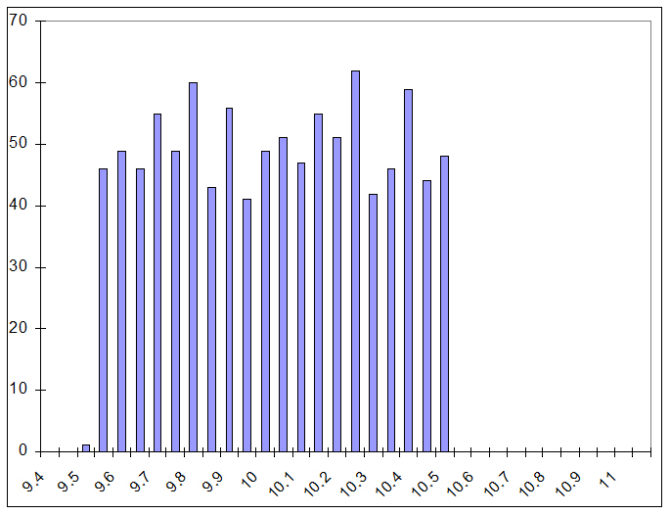 Rys. 5. Rozkład zmierzonych symulacyjnie pojemności z zastosowaniem funkcji mc
Rys. 5. Rozkład zmierzonych symulacyjnie pojemności z zastosowaniem funkcji mc
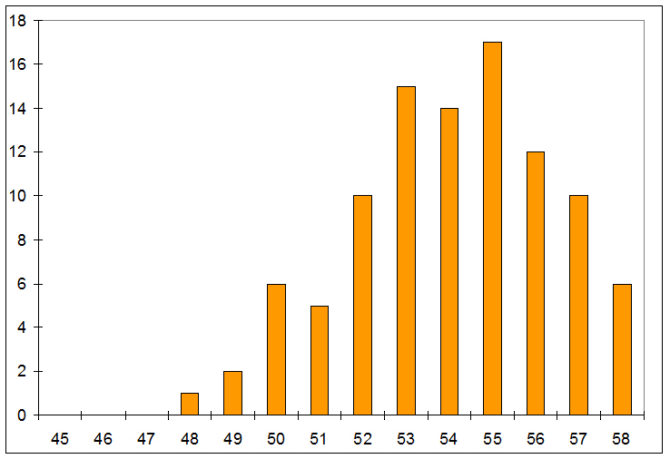 Rys. 6. Rozkład zmierzonych pojemności rzeczywistych kondensatorów 47 nF
Rys. 6. Rozkład zmierzonych pojemności rzeczywistych kondensatorów 47 nF
Symulacja z użyciem zmodyfikowanej funkcji mc
Symulacja rozrzutu wyników jakiegoś pomiaru z zastosowaniem standardowej funkcji mc daje z pewnością wyobrażenie o tym czego można się spodziewać w realizacji praktycznej, ale statystyka pomiaru rzeczywistego będzie jednak inna. Na szczęście LTspice ma funkcję biblioteczną gauss(sigma), której parametrem jest odchylenie standardowe rozkładu normalnego. Jak można się domyślać, funkcja generuje liczbę losową o rozkładzie normalnym z wartością oczekiwaną równą 0 i odchyleniem standardowym równym sigma. Wykorzystamy ją do zmodyfikowania bibliotecznej funkcji mc. Utworzymy własną funkcję mcg zdefiniowaną jako:
.func mcg(nomin,tol)= nomin*(1+gauss(tol/3))
Jak widać, jest to odpowiednik funkcji mc, generujący jednak wartości losowe z rozkładem normalnym, nie równomiernym. Ma ona takie same argumenty, tzn. wartość znamionową i tolerancję. Podzielenie tolerancji przez 3 wynika z przyjęcia założenia, że w przedziale wartość_znamionowa-tolerancja…wartość_znamionowa+tolerancja mieści się 99,73% generowanych losowo wartości. Zmierzymy jeszcze raz symulacyjnie pojemność tego samego kondensatora 10 nF z zastosowaniem funkcji mcg i za pomocą Excela wyznaczymy rozkład wyników. Schemat pomiarowy przedstawiono na rys. 7, a na rys. 8 uzyskany rozkład. Z całą pewnością możemy uznać, że jest to rozkład normalny. Interesujące może być jeszcze nałożenie na siebie poszczególnych pomiarów (rys. 9). Na takim wykresie wyraźnie uwidacznia się fakt, że przy bardziej naturalnym rozkładzie normalnym większość wyników jest skupiona względnie blisko wartości średniej, a tylko nieliczne znacznie się od niej oddalają.
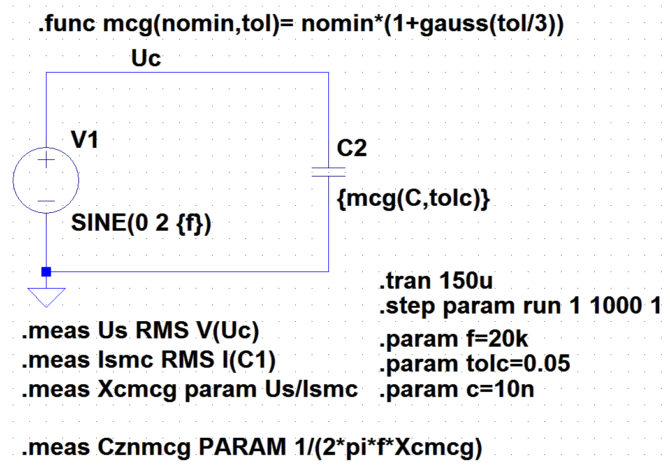 Rys. 7. Symulacyjny pomiar pojemności kondensatora funkcją mcg
Rys. 7. Symulacyjny pomiar pojemności kondensatora funkcją mcg
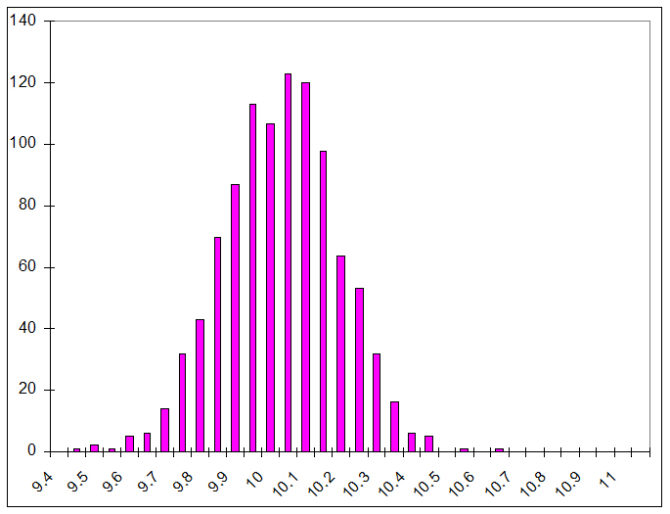 Rys. 8. Rozkład zmierzonych symulacyjnie pojemności z zastosowaniem funkcji mcg
Rys. 8. Rozkład zmierzonych symulacyjnie pojemności z zastosowaniem funkcji mcg
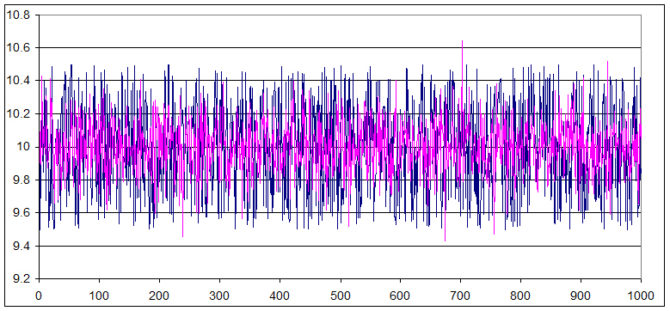 Rys. 9. Nałożone wyniki symulacyjnego pomiaru pojemności kondensatorów z zastosowaniem funkcji mc i mcg
Rys. 9. Nałożone wyniki symulacyjnego pomiaru pojemności kondensatorów z zastosowaniem funkcji mc i mcg
Symulacja mostka TT z zastosowaniem zmodyfikowanej funkcji mc, o nazwie mcg
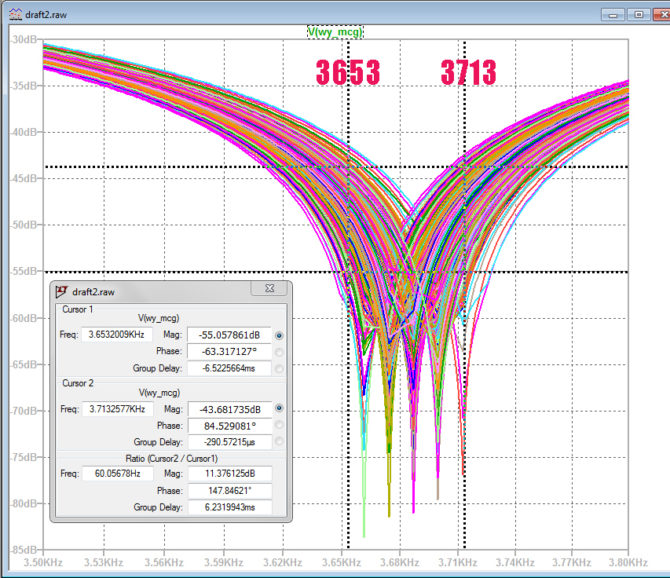
Gdyby interesowałby nas tylko zasięg rozrzutu częstotliwości środkowej mostka, funkcja biblioteczna mc powinna dać zadawalające wyniki. Jeśli jednak chcielibyśmy analizować statystykę wyników, bliższa prawdzie byłaby metoda symulacji z zastosowaniem funkcji mcg. Schemat pomiarowy przedstawiono na rys. 10. Okazuje się, że w tej metodzie częstotliwości środkowe mostka zawierają się w przedziale od 3653 do 3713 Hz (rys. 11).
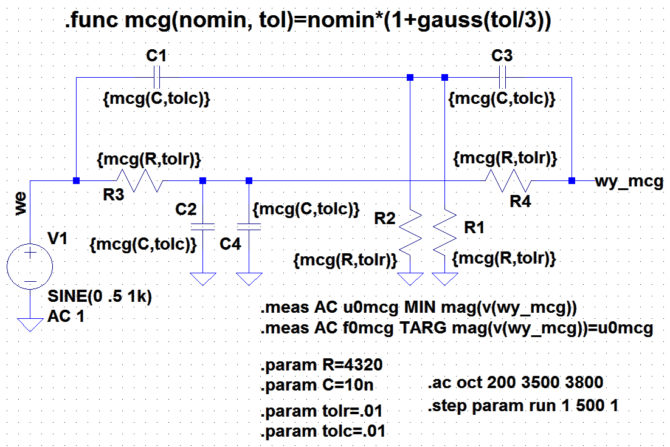 Rys. 10. Przygotowanie symulacji mostka TT z zastosowaniem funkcji mcg
Rys. 10. Przygotowanie symulacji mostka TT z zastosowaniem funkcji mcg
Symulacja metodą „Worst Case”
Jakby się dobrze zastanowić, można by popaść w pewną wątpliwość czy opisane metody mają sens? Przecież może się zdarzyć, i jest to wysoce prawdopodobne, że w przeprowadzonej sesji pomiarowej nie zostałaby wylosowana skrajna wartość wynikająca z tolerancji jakiegoś elementu, a nawet kilku z nich. Oznacza to, że w układzie rzeczywistym może wystąpić przypadek gorszy niż w symulacjach z zastosowaniem funkcji mc lub mcg. Jedynym rozwiązaniem wyłapania takich okoliczności jest symulacja metodą „Worst Case”. Nie interesują nas w niej wartości pośrednie elementów, a jedynie skrajne, wynikające z tolerancji. Zadanie wcale nie jest proste, gdyż trzeba uwzględnić kombinacje ekstremalnych wartości dla wszystkich elementów. Ręczne wprowadzanie parametrów raczej nie wchodzi w grę ze względu na dużą liczbę koniecznych poprawek. Poza tym łatwo można się przy tym pomylić.
Symulacja w LTSpice
Rozwiązanie problemu zaproponowali panowie Gabino Alonso i Joseph Spenser. Jak wiemy uruchomienie symulacji z komendą .step param run powoduje utworzenie zmiennej RUN, która określa numer sesji. Jeśli przyjmiemy, że liczba sesji byłaby tak dobrana, aby liczba cyfr w jej zapisie binarnym była równa liczbie badanych elementów, to każda z tych cyfr kodowałaby wartość przypisanego do niej elementu. Można to przedstawić za pomocą tabelki (rys. 12). Pozostaje już tylko przyjęcie jakiejś konwencji, np. jeśli cyfra jest równa 1, to wartość elementu jest równa najmniejszej możliwej wynikającej z tolerancji, dla cyfry 0 jest to wartość największa. Funkcję, która realizuje tę ideę nazwiemy wc. Ma ona, tak jak mc i mcg, argumenty zawierające wartość znamionową i tolerancję, ale jest też dodatkowy argument będący unikatową liczbą przypisaną do danego elementu. Indeks ten musi być ręcznie nadawany każdemu elementowi i nie można się przy tym pomylić. Idea jest zrealizowana za pomocą dwóch zdefiniowanych samodzielnie funkcji:
- .func wc(nom, tol, ind) if(run==0,nom,if(binary(ind),nom*(1-tol),nom*(1+tol))) – jest to zasadnicza funkcja „Worst Case” ustalająca wartość elementu w zależności od jego indeksu i pośrednio od numeru sesji,
- .func binary(i) floor(run/(2**i))-2*floor(run/(2**(i+1))) – funkcja kodująca binarnie numer sesji. Użyto w niej biblioteczną funkcję floor, która zwraca największą liczbę całkowitą nie większą od argumentu funkcji.
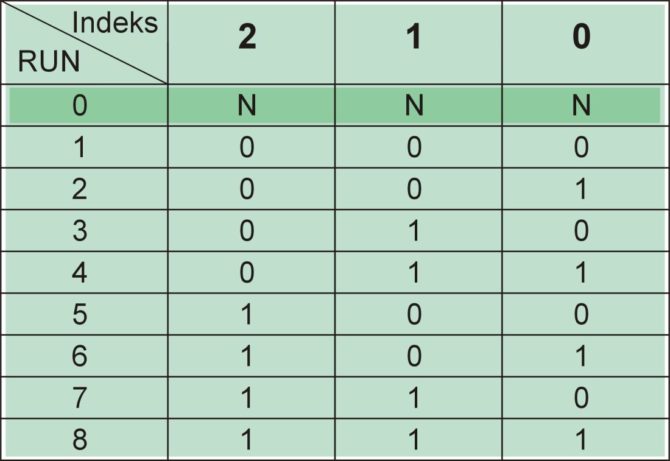 Rys. 12. Binarne kodowanie zmiennej RUN stosowane w symulacji Worst Case
Rys. 12. Binarne kodowanie zmiennej RUN stosowane w symulacji Worst Case
W symulowanym mostku (rys. 13) jest 8 elementów, co oznacza, że wymagana liczba sesji powinna być równa 28=256. Funkcja wc uwzględnia jednak również przypadek, w którym nadawana jest wartość nominalna elementu. Występuje on dla zmiennej RUN równej 0. Ostatecznie symulacja jest uruchamiana z komendą .step param RUN 0 257 1. Wyniki przedstawiono na rys. 14. Zgodnie z przewidywaniami zakres rozrzutu częstotliwośi środkowych flitru jest w tym przypadku największa: od 3611 do 3757.
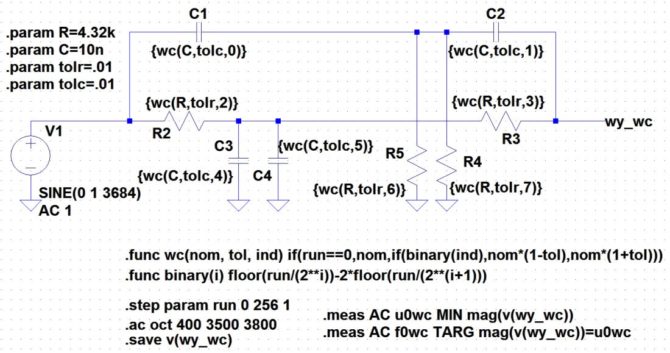 Rys. 13. Przygotowanie symulacji mostka TT metodą Worst Case
Rys. 13. Przygotowanie symulacji mostka TT metodą Worst Case
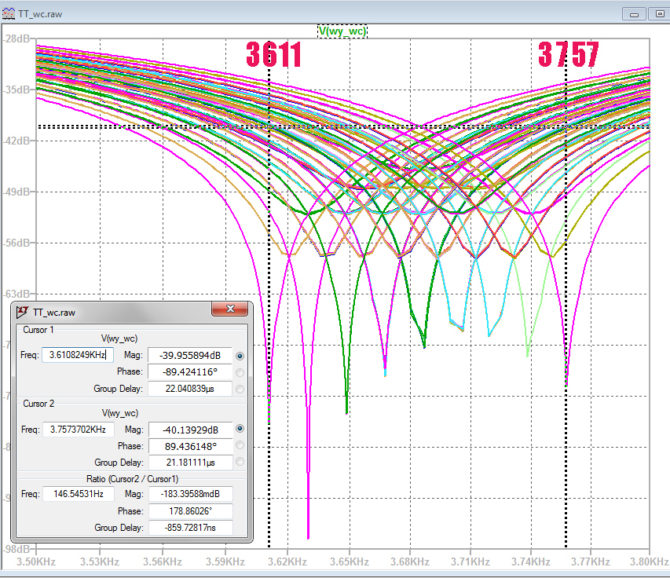 Rys. 14. Wyniki symulacji Worst Case
Rys. 14. Wyniki symulacji Worst Case
Pomiary układu rzeczywistego
Nadszedł oczekiwany moment konfrontacji teorii z praktyką. Na dodatkowej płytce Analog Training board zostało zmontowanych 10 filtrów TT. Nie jest to wprawdzie zbyt duża próba statystyczna, ale jakieś wnioski z pomiaru powinno dać się wyciągnąć. Pomiary prowadzimy z zastosowaniem zestawu Analog Discovery 2 i programu WaveForms. Ze względu na konieczność rozgałęzienia sygnału z wyjścia 1. kanału generatora arbitralnego AD2 konieczne jest użycie np. dodatkowego breadboardu (rys. 15).
Do wyjścia generatora dołączamy wejście 1. kanału oscyloskopu, a także kabelek, który będzie przełączany do kolejnych wejść mostków TT. Do wyjść mostków również przełączamy wejście 2. kanału oscyloskopu. Uruchamiamy narzędzie „Network” i za jego pomocą zdejmujemy charakterystyki częstotliwościowe każdego filtru. Przyjmujemy, że częstotliwość pomiarowa będzie się zmieniać w zakresie od 3500 Hz do 3800 Hz. Ważne jest ustawienie dość dużego napięcia generatora, co najmniej 2 V, gdyż musimy pamiętać, że poziom sygnału dla częstotliwości środkowej może być bardzo mały. Warto również wybrać liniową skalę dla osi częstotliwości, gdyż taka była użyta w symulacjach. Wiemy z nich, że charakterystyki mają dość strome nachylenia, więc konieczne jest przyjęcie co najmniej 500 punktów pomiarowych. Wynik każdej symulacji zapisujemy jako przebieg referencyjny. Uzyskujemy tym samym rodzinę charakterystyk podobną do tej z symulacji, tylko mniej liczną (rys. 16).
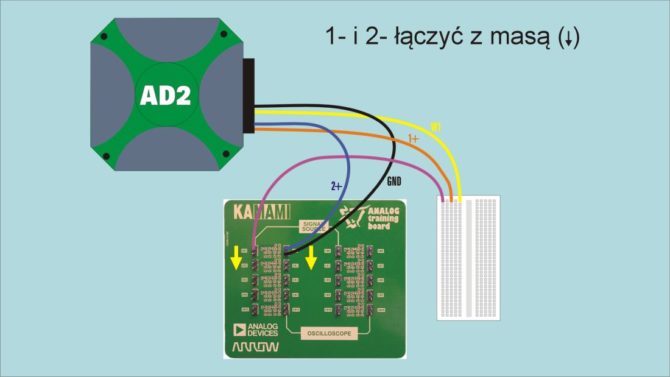 Rys. 15. Schemat połączeń układu do pomiarów mostków TT
Rys. 15. Schemat połączeń układu do pomiarów mostków TT
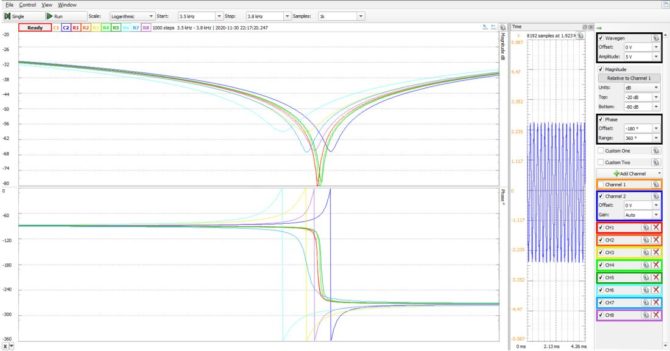 Rys. 16. Wyniki pomiarów rzeczywistych mostków TT
Rys. 16. Wyniki pomiarów rzeczywistych mostków TT
Wnioski
Na rys. 17 zestawiono wyniki wszystkich symulacji i pomiarów. Okazuje się, że rozrzut częstotliwości środkowych mostków TT zamontowanych na płytce treningowej był dużo mniejszy niż moglibyśmy się tego spodziewać na podstawie symulacji. Różnica między największą i najmniejszą częstotliwością wynosiła zaledwie 19 Hz, co należy traktować jako bardzo dobry rezultat. Symulacja metodą Monte Carlo przygotowała nas na rozrzut 90-hercowy, a zastosowanie funkcji mcg zawęziło ten zakres do 60 Hz. Prawdziwie dramatycznie wyglądają wyniki dla najgorszego przypadku. Zakres rozrzutu częstotliwości mostka rozciąga się na 146 Hz. Pocieszeniem jest jednak fakt, że prawdopodobieństwo zmontowania mostka z elementów o skrajnie niekorzystnych wartościach jest bardzo niewielkie, ale… nie można go wykluczyć.
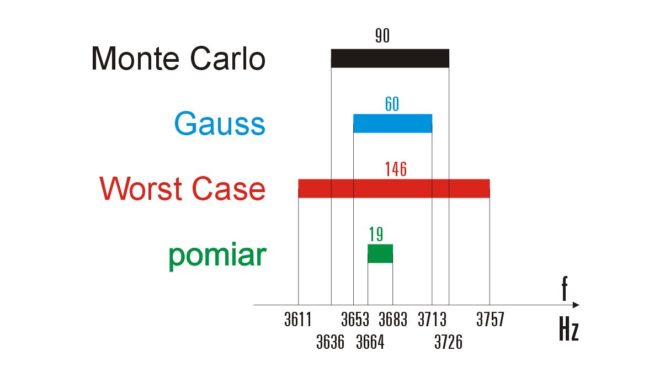 Rys. 17. Zestawienie wyników wszystkich symulacji i pomiarów mostków TT
Rys. 17. Zestawienie wyników wszystkich symulacji i pomiarów mostków TT
Skoro metoda „Worst Case” daje niezbyt dobre wyniki nawet dla precyzyjnych, 1-procentowych elementów, to strach pomyśleć, co będzie się działo, gdy zastosujemy elementy o większej tolerancji. Ciekawość jest jednak silniejsza od strachu. Okazuje się, że przy użyciu rezystorów 5% i kondensatorów 10% możemy spodziewać się (wg, metody mcg) rozrzutu częstotliwości środkowych filtrów w przedziale od 3515 do 3956. Metoda „Worst Case” dała wynik 3204…4329. Zupełnie nie do przyjęcia.






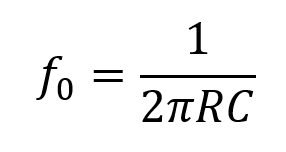
 Caroline Pannier – nowa dyrektorka targów electronica – analizuje sytuację gospodarczą branży i przedstawia wyniki
Caroline Pannier – nowa dyrektorka targów electronica – analizuje sytuację gospodarczą branży i przedstawia wyniki  Konstrukcja Ventiva Zoned Cooling™ – ukierunkowane chłodzenie powietrza dla urządzeń AI Edge
Konstrukcja Ventiva Zoned Cooling™ – ukierunkowane chłodzenie powietrza dla urządzeń AI Edge  Komunikacja dalekiego zasięgu oparta na technologii Qualcomm dla robotyki i dronów
Komunikacja dalekiego zasięgu oparta na technologii Qualcomm dla robotyki i dronów 






