Oscyloskopy cyfrowe wyparły już niemal całkowicie oscyloskopy analogowe. Obsługując je nie zawsze pamiętamy o pewnych subtelnych różnicach w działaniu obu klas przyrządów. Wprawdzie zarówno oscyloskopy analogowe, jak i cyfrowe umożliwiają obserwację przebiegów w czasie, lecz zasada ich tworzenia jest zgoła odmienna. Czasami czyhają na nas różne pułapki.

Niekwestionowaną zaletą oscyloskopów cyfrowych jest wszechstronna analiza przebiegów, możliwa dzięki przetworzeniu sygnału analogowego na cyfrowy. Dysponując cyfrowym zapisem sygnału można z łatwością obliczyć jego amplitudę, wartość skuteczną, częstotliwość, czasy narastania i opadania zboczy, współczynnik wypełnienia przebiegu prostokątnego i szereg innych parametrów, a nawet dokonać analizy widmowej. Nawet najprostsze oscyloskopy cyfrowe mają zwykle co najmniej kilkanaście funkcji pomiarowych. Używając ich nierozważnie można jednak nieświadomie popełniać spore błędy.

Coś tu nie gra

Rozważmy taki przykład: obserwujemy na oscyloskopie przebieg sinusoidalny o nieznanej częstotliwości. Załóżmy, że chcemy tę częstotliwość określić na podstawie obserwacji widma sygnału w oknie FFT. Chcąc uzyskać dużą rozdzielczość pomiaru staramy ustawić jak najdłuższą podstawę czasu w oscyloskopie. Niech to będzie np. 50 ms/dz. Przebieg w oknie czasowym jest bardzo gęsty, prawie nic na nim nie widać, ale od czego mamy okno „Zoom”. Za to w oknie FFT otrzymujemy bardzo wąski i wyraźny prążek widmowy sygnału (rys. 1). Odczytujemy, że wypada on na częstotliwości 4 kHz.

Jesteśmy zadowoleni z pomiaru i już chcemy podzielić się nim z kolegami po fachu, ale dla świętego spokoju zobaczmy jeszcze, co się stanie gdy podciągniemy nieznacznie częstotliwość sygnału do góry.  I… co to? Czy coś się stało z oscyloskopem, a może generator nawalił? Po przestrojeniu generatora „w górę” prążek widmowy przesunął się w lewo, w kierunku niższych częstotliwości (rys. 2). Nie, to nie jest sytuacja nienormalna, trzeba tylko mieć świadomość popełnionego błędu.

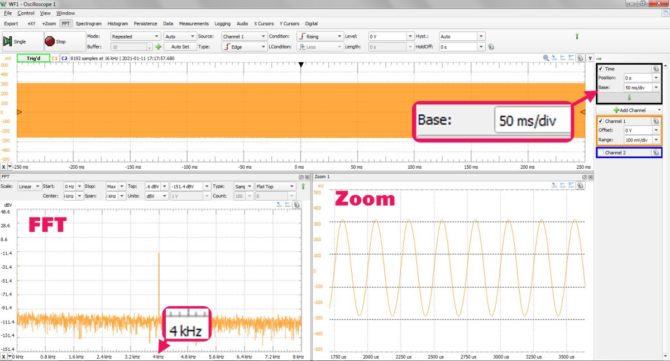Rys. 1. Nieprawidłowo wyświetlony w oknie FFT prążek widma sygnału

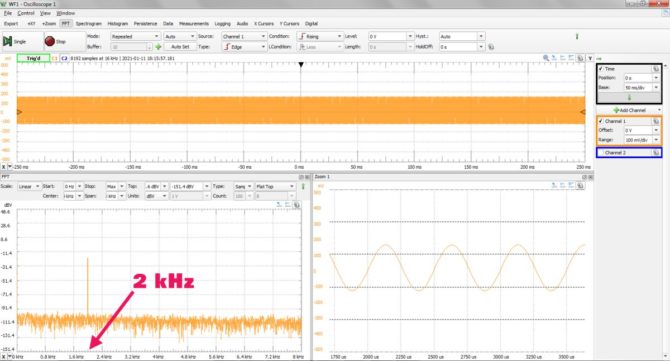Rys. 2. Prążek widma przesunięty w kierunku niższych częstotliwości po podwyższeniu częstotliwości sygnału mierzonego

Twierdzenie o próbkowaniu

W roku Wielkiej Rewolucji Październikowej (1917), a więc na długo przed powstaniem pierwszego przetwornika analogowo-cyfrowego, pracujący w Stanach Zjednoczonych Szwed z pochodzenia, Harry Theodor Nyquist opublikował w jednym z czasopism twierdzenie, które stało się fundamentalnym twierdzeniem dotyczącym cyfrowego przetwarzania sygnałów analogowych. Wówczas nie istniało jeszcze takie pojęcie, a prace teoretyczne o zbliżonej tematyce były możliwe dzięki rozwijaniu istniejącej już telegrafii. Wkrótce do zespołu Nyquista dołączył matematyk z wykształcenia Claude Shannon. Twierdzenie nabrało znaczenia praktycznego i obecnie jest znane jako twierdzenie Nyquista-Shannona. Do autorstwa podobnego twierdzenia, w dodatku jak podaje autor ogłoszonego wcześniej, przyznaje się również rosyjski fizyk Władimir Kotielnikow.

Twierdzenie o próbkowaniu Nyquista-Shannona, czy też Kotielnikowa mówi, że do prawidłowego odtworzenia sygnału analogowego na podstawie ciągu utworzonego z jego próbek konieczne jest zapewnienie warunku, aby częstotliwość próbkowania była co najmniej dwukrotnie wyższa od najwyższej składowej widma sygnału analogowego. Niespełnienie tego warunku skutkuje powstaniem składowych o fałszywych częstotliwościach, nieistniejących w widmie wyjściowego sygnału analogowego.

Graficzna interpretacja zjawiska aliasingu

Dla uproszczenia analizy zakładamy, że mamy do czynienia z czystą sinusoidą o częstotliwości f_s. Najpierw rozpatrzymy przypadek, w którym sinusoida ta będzie próbkowana z częstotliwością f_p znacznie większą od częstotliwości f_s (rys. 3). Proces przetwarzania cyfrowego składa się z dwóch etapów: próbkowania, czyli wyznaczania momentów, w których są pobierane próbki sygnału oraz kwantyzacji, w którym próbkom nadawana jest wartość odpowiadająca wartości sygnału w chwili próbkowania. Tworzony w ten sposób zbiór danych liczbowych pozwala na późniejsze odtworzenie na ich podstawie sygnału oryginalnego. Dzięki tak gęstemu próbkowaniu przebieg powinien być odtworzony z próbek bardzo dokładnie, na czym nam oczywiście zależy, ale jak to zwykle w technice bywa, konieczne jest czasami podejmowanie pewnych kompromisów.

W tym przypadku problematyczna staje się wymagana szybkość przetwornika analogowo-cyfrowego, szczególnie podczas obróbki sygnałów o dużej częstotliwości. Kłopotów można spodziewać się również z gromadzeniem dużych ilości danych cyfrowych, nie mówiąc już o szybkości ich obsługi. Dlatego w praktyce dążymy do jak największego spowolnienia szybkości próbkowania, takiego jednak, by na podstawie próbek możliwe było prawidłowe odtworzenie sygnału.

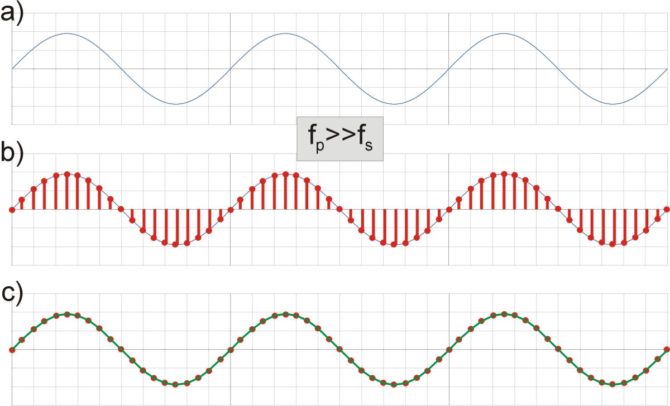Rys. 3. Próbkowanie z częstotliwością wielokrotnie wyższą od częstotliwości sygnału

Różne częstotliwości próbkowania

Na rys. 4a przedstawiono sytuację, w której częstotliwość próbkowania jest 3,33 razy większa od częstotliwości sygnału. Stosując najprostszą metodę odtwarzania przebiegu, jaką jest interpolacja liniowa polegająca na bezpośrednim łączeniu próbek, uzyskujemy przebieg, który tylko przypomina oryginał. Istnieją jednak metody pozwalające uzyskiwać znacznie lepsze odtwarzanie przebiegu oryginalnego. Jest nią na przykład powszechnie stosowana nieliniowa interpolacja sin(x)/x.

Przypadek krytyczny, w którym częstotliwość próbkowania jest dokładnie 2 razy większa od częstotliwości sygnału przedstawiono na rys. 4b. No cóż, stosując interpolację liniową odtworzony przebieg ma kształt trójkątny, ale jego częstotliwość podstawowa jest dokładnie taka sama jak oryginału. Stosując interpolację nieliniowa można uzyskać przebieg zbliżony do wyjściowego. Warto jednak zauważyć, że amplituda odtworzonego przebiegu zależy od momentów próbkowania. W najgorszym przypadku, gdy próbki wypadają w węzłach sinusoidy nie otrzymamy żadnego przebiegu, dokładniej odtworzony przebieg będzie miał wartość zerową.

Jeśli częstotliwość próbkowania będzie niższa od dwukrotnej częstotliwości sygnału oryginalnego (rys. 4c), odtworzony przebieg będzie miał częstotliwość mniejszą niż oryginał. W takim przypadku przy zastosowaniu interpolacji nieliniowej możliwe jest uzyskanie bardzo ładnego sygnału, z tym że będzie to sygnał fałszywy. Mamy do czynienia z aliasingiem.

Rys. 4. Próbkowanie z częstotliwością a) 3,33 razy większą od częstotliwości sygnału, b) dwukrotnie wyższą od częstotliwości sygnału, c) mniejszą niż dwukrotna częstotliwość sygnału

Aliasing w ujęciu widmowym

Popatrzmy jeszcze na widmową interpretację aliasingu. Na rys. 5a przedstawiono widmo pewnego sygnału poddanego próbkowaniu z częstotliwością wielokrotnie wyższą od najwyższej częstotliwości tego sygnału. Widmowym efektem próbkowania, podobnie jak w modulacji amplitudowej, jest skopiowanie widma obustronnie wokół częstotliwości modulującej i jej wielokrotności. Jak wynika z rys. 5a wszystkie składniki widma występują samodzielnie i nie nakładają się na siebie. Nie wywołuje to żadnych skutków ubocznych, ale jak już wiemy, zależy nam na jak największym obniżeniu częstotliwości próbkowania. Można to robić bezpiecznie aż do momentu, gdy połowa częstotliwości próbkowania nie znajdzie się w zakresie widma sygnału oryginalnego (rys. 5b).

W sytuacji z rys. 5c mamy już do czynienia z aliasingiem. Jeden z listków widma powstałego w wyniku próbkowania pokrywa się z widmem oryginalnym. Podczas odtwarzania sygnału analogowego z próbek uzyskanych w tym procesie należy spodziewać się składowych fikcyjnych. Problem jest o tyle groźny, że składowe aliasingowe mogą mieć amplitudy takie, jak w pełni użytkowy sygnał. Jeśli nie mamy świadomości błędu popełnionego w procesie próbkowania możemy sądzić, że tak może wyglądać sygnał oryginalny.

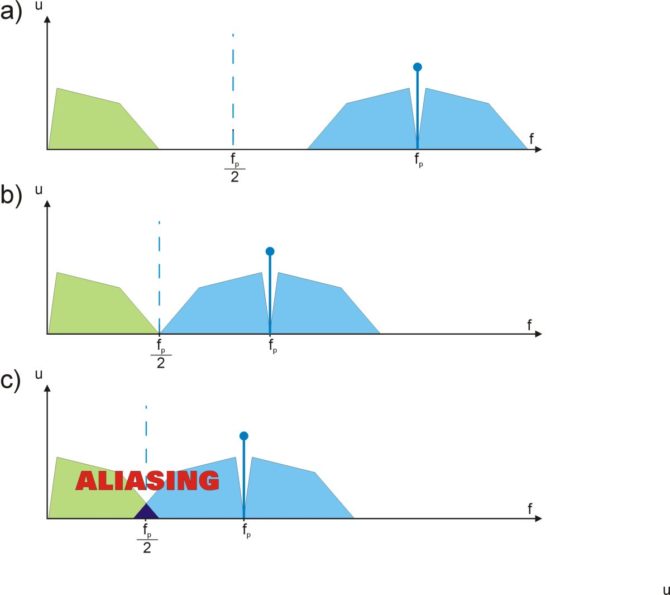Rys. 5. Widmowa interpretacja aliasingu a) fp>>ts, b) fp=2fs, c) f_p<2f_s

Jak można uniknąć aliasingu?

Pierwszą metodą jest zastosowanie odpowiednio wysokiej częstotliwości próbkowania. Można tak postąpić, jeśli dobrze znamy widmo sygnału próbkowanego. Jeżeli nie można dowolnie podnosić częstotliwości próbkowania, albo jeżeli nie znamy widma sygnału poddawanego próbkowaniu, najlepszym rozwiązaniem jest ograniczenie go do zakresu f_p/2 (połowy częstotliwości próbkowania). Konieczne jest więc zastosowanie dodatkowego elementu w układzie akwizycji sygnału, jakim jest dolnoprzepustowy filtr antyaliasingowy. Musi on być zastosowany koniecznie przed przetwornikiem analogowo-cyfrowym, gdyż umieszczenie go za nim już nic nie da. Idealny filtr antyaliasingowy miałby charakterystykę prostokątną, tzn. przepuszczałby sygnał w całości od zera do f_p/2, a powyżej już nie przepuszczał nic. Oczywiście budowa takiego filtru jest niemożliwa, więc znowu muszą być podjęte pewne kompromisy.

Filtry fizyczne mają charakterystykę częstotliwościową zależną od ich rzędu. Każdy rząd wprowadza zmianę spadku charakterystyki o 20 dB/dekadę (6 dB/oktawę). Przykłady przedstawiono na rys. 6. Kompromis polega na optymalnym dobraniu rzędu filtru i jego 3-decybelowej częstotliwości granicznej. Filtr antyaliasingowy powinien całkowicie stłumić sygnał próbkowany dla częstotliwości f_p/2. Jak mocno powinien go tłumić zależy przede wszystkim od rozdzielczości próbkowania i związanej z tym dynamiki przetwornika. Przykładowo, przetwornik 12-bitowy ma rozdzielczość ok. 72 dB, więc o tyle powinien być stłumiony sygnał dla częstotliwości f_p/2. Jeśli od tego wyjdziemy to łatwo już można obliczyć jaką powinien mieć częstotliwość graniczną. Oczywiście im wyższy będzie rząd filtru, tym ta częstotliwość będzie bliższa f_p/2, a więc taki filtr zbliży się do ideału.

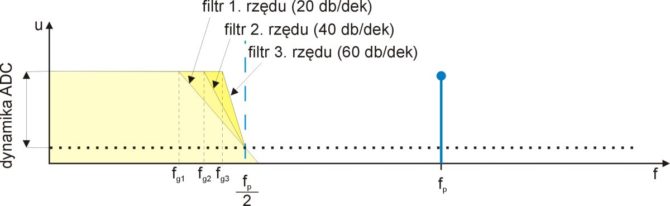Rys. 6. Ilustracja zasady projektowania filtru antyaliasingowego

Przykładowa realizacja filtru antyaliasingowego

Przyjmijmy, że będziemy rozpatrywać sygnał o paśmie nie przekraczającym 20, 30 Hz. Poddamy go próbkowaniu w układzie z przetwornikiem 12-bitowym. Zastosujemy filtr antyaliasingowy 2. rzędu o częstotliwości granicznej 8,5 Hz. Niestety, taki filtr teoretycznie tłumi sygnał o 72 dB dopiero przy częstotliwości ok. 450 Hz, a jest to daleko poza pasmem naszego sygnału. Schemat ideowy przedstawiono na rys. 7. Filtr o strukturze Sellena-Key’a oparto na układzie OP491. W prezentowanym przykładzie nie zależy nam na wielkiej precyzji, do budowy użyjemy więc rezystorów i kondensatorów 10-procentowych. Z obliczeń wynika, że elementy powinny mieć wartości: R₁=24,4 kΩ, R₂=96 kΩ, C₁=220 nF, C₂=680 nF. Układ jest zasilany dwoma napięciami (+5 V i –5 V). Na rys. 7 przedstawiono połączenia dwóch kanałów oscyloskopu i generatora filtrowanego sygnału, który następnie będzie próbkowany.

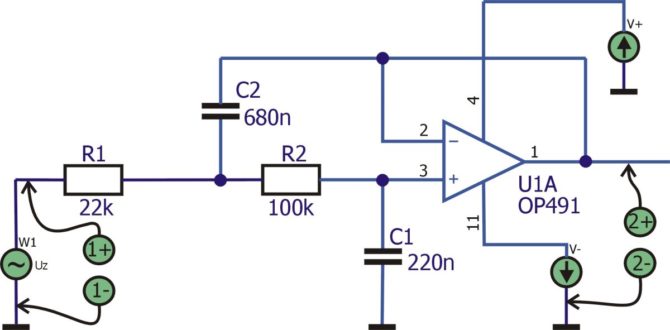Rys. 7. Filtr dolnoprzepustowy 2. rzędu o częstotliwości granicznej 8,5 Hz

Symulacja filtru

Przed przystąpieniem do budowy filtru przeprowadzimy jego symulację, w której sprawdzimy czy rzeczywiście ma zakładane parametry. Schemat narysowany w edytorze programu LTspice oraz wynik symulacji AC przedstawiono na rys. 8. Zastosowano symulację AC Analysis, w której przyjęto 200 punktów na oktawę, częstotliwość początkową 1 Hz i końcową 1 kHz. Po uruchomieniu symulacji wskazujemy wyjście układu jako punkt, do którego ma być odniesiony wykres. Po chwili na ekranie zostaje wyświetlona charakterystyka częstotliwościowa filtru. Ustawiamy 1. kursor pomiarowy gdzieś na początku, w okolicy 1 Hz, kursor 2. natomiast ustawiamy w punkcie, któremu odpowiada spadek sygnału o 3 dB. Jak wynika z wyświetlonych parametrów kursorów częstotliwość graniczna filtru wynosi 8,46 Hz, a więc z grubsza zgodnie z założeniami.

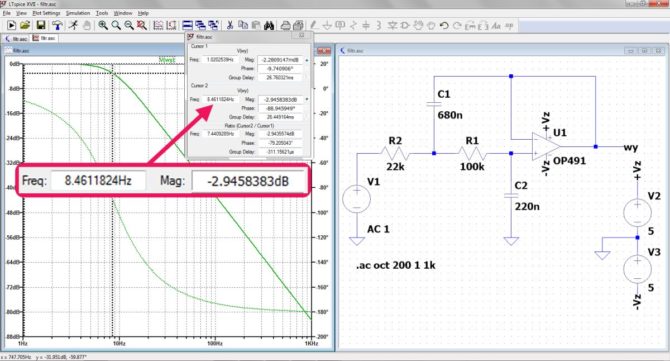Rys. 8. Wyniki symulacji filtru w programie LTspice – pomiar częstotliwości granicznej

Sprawdzimy jeszcze czy spadek charakterystyki wynosi 12 dB/oktawę, co odpowiada 40 dB/dekadę. Ustawiamy kursor 1. na częstotliwości np. 100 Hz, kursor 2. natomiast na częstotliwości 2-krotnie mniejszej (oktawa), czyli na 50 Hz. W polu „Mag” tabelki opisującej kursory odczytujemy 12,0 dB (rys. 9), co potwierdza założenia. Mamy zatem rzeczywiście filtr 2. rzędu o częstotliwości granicznej ok. 8,5 Hz.

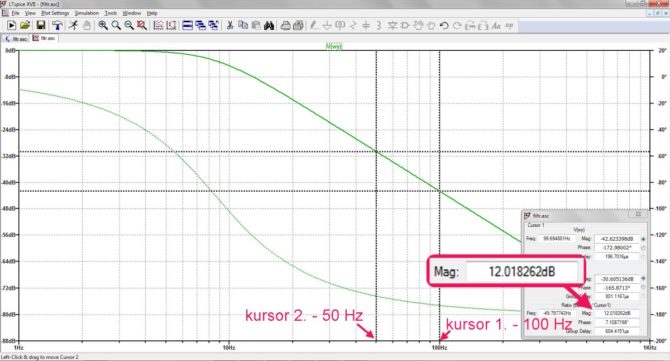Rys. 9. Wyniki symulacji filtru w programie LTspice – pomiar szybkości opadania charakterystyki

Próbkowanie z różnymi parametrami

Po wstępie teoretycznym możemy przystąpić do eksperymentów praktycznych. Najpierw weryfikujemy charakterystykę filtru, który budujemy na breadboardzie (rys. 10). W programie WaveForms uruchamiamy narzędzie Network. Ustawiamy parametry: Start=1 Hz, Stop=1 kHz, Offset=0 V, Amplitude=1 V, Top=10 dB, Bottom=-90 dB, Phase offset=0°, Range=360°, wybieramy Sample=100, włączamy podgląd czasowy przebiegu i uruchamiamy jednorazowy pomiar. Jego wynik przedstawiono na rys. 11. Okazuje się, że mierzony filtr ma częstotliwość graniczną 8,995 Hz i spadek charakterystyki 12,0399 dB/okt, co potwierdza obliczenia i wyniki symulacji.

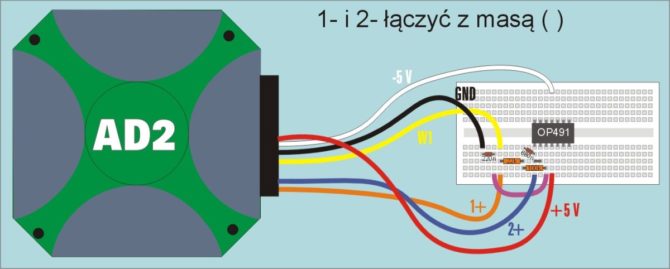Rys. 10. Schemat montażowy układu pomiarowego filtru antyaliasingowego

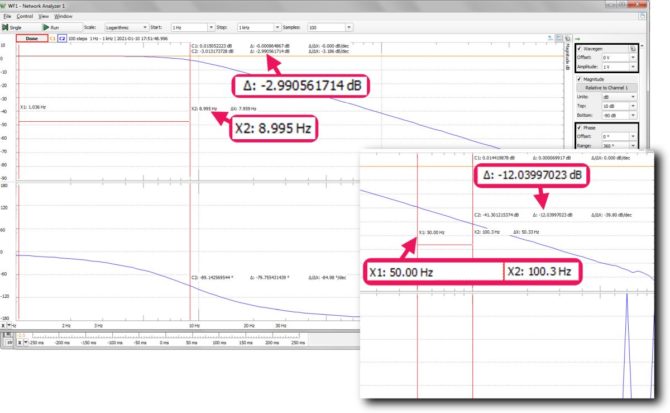Rys. 11. Wyniki pomiarów filtru antyaliasingowego

Teraz kanał 1. generatora zestawu Analog Discovery 2 dołączamy do wejścia urządzenia z przetwornikiem analogowo-cyfrowym. Sygnał analogowy jest w nim przetwarzany na sygnał cyfrowy, a następnie przesyłany do komputera, który za pomocą odpowiedniego oprogramowania wizualizuje przebieg na ekranie (rys. 12).

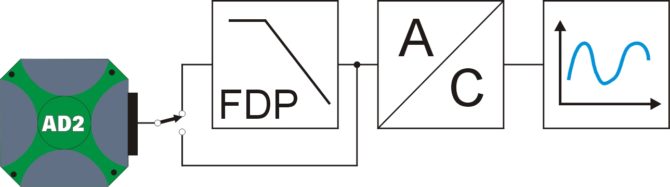Rys. 12. Układ cyfrowego przetwarzania sygnału

W pierwszym kroku cały proces przeprowadzimy z pomięciem filtru antyaliasingowego. Badamy sygnał sinusoidalny o częstotliwości 10 Hz, który próbkujemy z częstotliwością 400 Hz. Mamy zatem 40 próbek na okres, spodziewamy się więc bardzo dokładnego odwzorowania przebiegu nawet bez stosowania interpolacji nieliniowej. Program wizualizujący tworzy wykresy z użyciem najprostszej interpolacji liniowej. Rzeczywiście, sinusoida wyświetlona na ekranie wygląda bardzo ładnie, niemal idealnie (rys. 13), jej częstotliwość 10 Hz została odtworzona bezbłędnie. Po obniżeniu częstotliwości próbkowania do 50 Hz sytuacja z punktu widzenia twierdzenia o próbkowaniu jest nadal prawidłowa, ale odtworzony przy użyciu interpolacji liniowej przebieg wyraźnie już różni się od oryginału (rys. 14).

Podwyższanie częstotliwości sygnału

Idąc dalej, podwyższamy częstotliwość sygnału do 40 Hz. Mamy świadomość, że popełniamy karygodny błąd, ale czynimy to świadomie w celach, nazwijmy to, naukowych. Na ekranie widzimy wyraźny przebieg, przyjmijmy, że jest to nadal sinusoida, o częstotliwości… 10 Hz (rys. 15). Nie, to nie jest błąd. Wiemy już, że mamy do czynienia z aliasingiem. Z czystej ciekawości, z premedytacją zwiększamy jeszcze częstotliwość sygnału aż do 49 Hz. Uzyskujemy piękną, a nawet przepiękną sinusoidę o częstotliwości 1 Hz (rys. 16). Wiemy jednak, że jest to fałszywy przebieg. Na pewno nie jest to sygnał oryginalny.

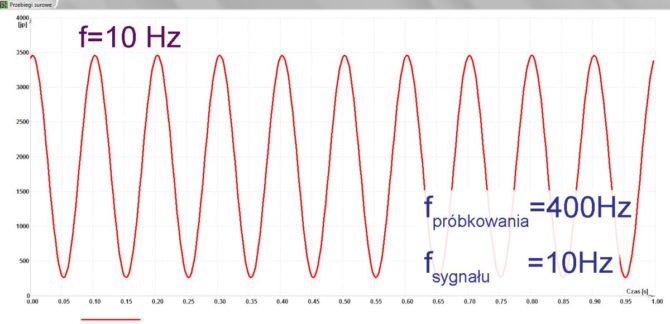Rys. 13. Przetwarzanie sygnału o częstotliwości 10 Hz przy próbkowaniu 400 Hz

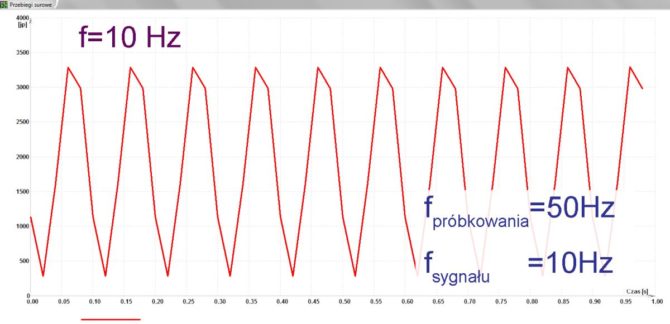Rys. 14. Przetwarzanie sygnału o częstotliwości 10 Hz przy próbkowaniu 50 Hz

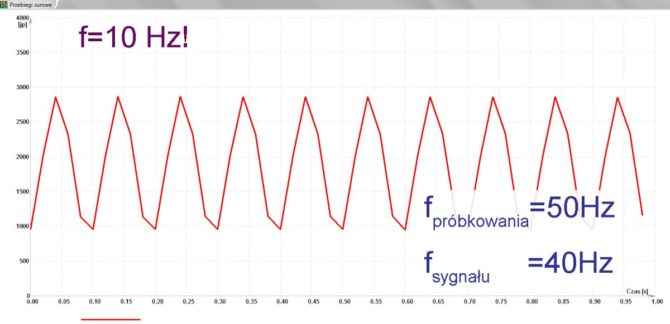Rys. 15. Przetwarzanie sygnału o częstotliwości 40 Hz przy próbkowaniu 50 Hz

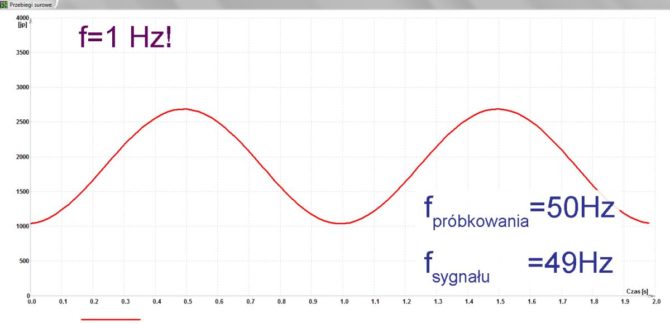Rys. 16. Przetwarzanie sygnału o częstotliwości 49 Hz przy próbkowaniu 50 Hz

Musimy jeszcze sprawdzić, w jakim stopniu tym wszystkim nieprawidłowościom zapobiegnie filtr anyaliasingowy. Włączamy go do układu między generator a przetwornik i powtarzamy pomiar. Pozostawiamy częstotliwość sygnału 1 Hz i częstotliwość próbkowania 50 Hz. Tym razem uzyskujemy niemal całkowicie płaski przebieg. Można się dopatrzyć jedynie śladowych ilości aliasingu (rys. 17). Można więc powiedzieć, że filtr spełnił swoje zadanie.

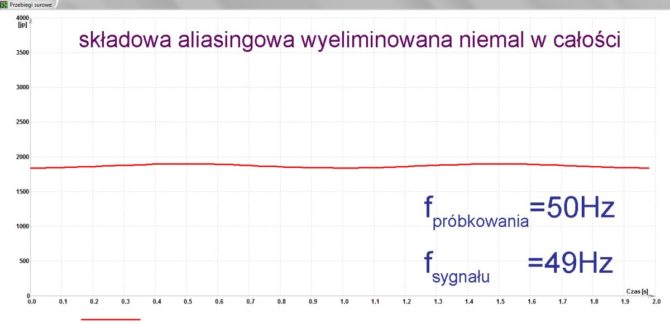Rys. 17. Przetwarzanie sygnału o częstotliwości 49 Hz przy próbkowaniu 50 Hz z zastosowaniem filtru antyaliasingowego

Aliasing w symulacji

Można zadać sobie pytanie, czy aliasing jest możliwy do przewidzenia w symulacji? Sprawdźmy to.

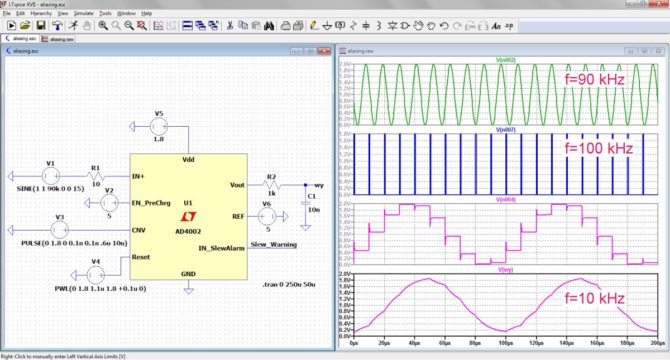
Do symulacji aliasingu zastosujemy przetwornik analogowo-cyfrowy AD4002, którego uproszczony model znajduje się w bibliotece LTspice. Schemat układu pomiarowego przedstawiono na rys. 18. Układ jest zasilany napięciem 1,8 V podawanym do wyprowadzenia Vdd. Należy ponadto doprowadzić napięcie 5 V do wyprowadzeń En_PreChrg i REF. Sygnałem przetwarzanym jest przebieg sinusoidalny o częstotliwości 90 kHz i amplitudzie 1 V z offsetem 1 V, który jest generowany przez źródło V1 i podawany przez rezystor 10 W do wejścia In+. Do wejścia CNV należy doprowadzić przebieg impulsowy taktujący przetwarzaniem. Są to impulsy o napięciu 1,8 V i czasie trwania 0,6 ms, generowane z częstotliwością 100 kHz (okres 10 ms).

Wiedząc już wszystko o aliasingu spodziewamy się uzyskać na wyjściu przetwornika sygnał o częstotliwości 10 kHz, który oczywiście będzie sygnałem fałszywym. Przebieg wyjściowy jest filtrowany w prostym filtrze R2, C1, który jednak ma na celu jedynie wygładzenie przebiegu wyjściowego i nie ma żadnego związku z eliminacją aliasingu. Jak już było powiedziane, gdybyśmy chcieli taki zabieg przeprowadzić, filtr musiałby być zastosowany po stronie wejściowej.

Na rysunku przedstawiono także najważniejsze przebiegi w układzie. Mierząc częstotliwość ostatniego z nich okazuje się, że jest ona równa 10 kHz. Mamy zatem aliasing.

Rys. 18. Symulacja aliasingu w programie LTspice